Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T06:21:52.402Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTABILITY AND UNCOUNTABLE LINEAR ORDERS II: DEGREE SPECTRA

Published online by Cambridge University Press:  13 March 2015

NOAM GREENBERG ,
ASHER M. KACH ,
STEFFEN LEMPP  and
DANIEL D. TURETSKY
NOAM GREENBERG
Affiliation:
DEPARTMENT OF MATHEMATICS, VICTORIA UNIVERSITY OF WELLINGTON, WELLINGTON, NEW ZEALANDE-mail: [email protected]: http://homepages.mcs.vuw.ac.nz/∼greenberg/
ASHER M. KACH
Affiliation:
DEPARTMENT OF MATHEMATICS, UNIVERSITY OF CHICAGO, CHICAGO, IL 60637, USA, E-mail: [email protected]
STEFFEN LEMPP
Affiliation:
DEPARTMENT OF MATHEMATICS, UNIVERSITY OF WISCONSIN MADISON, WI 53706-1388, USAE-mail: [email protected]: http://www.math.wisc.edu/∼lempp/
DANIEL D. TURETSKY
Affiliation:
KURT GÖDEL RESEARCH CENTER, UNIVERSITY OF VIENNA, 1090 VIENNA, AUSTRIAE-mail: [email protected]: http://tinyurl.com/dturetsky
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the computable structure theory of linear orders of size 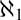$\aleph _1 $ within the framework of admissible computability theory. In particular, we study degree spectra and the successor relation.

Keywords

Primary: 03D60secondary: 03C57uncountable linear orderscomputabilitycomputable categoricity
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 1 , March 2015 , pp. 145 - 178
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ash, Christopher J., Jockusch, Carl G. Jr., and Knight, Julia F., Jumps of orderings. Transactions of the American Mathematical Society, vol. 319 (1990), no. 2, pp. 573–599.Google Scholar
Ash, Christopher J. and Knight, Julia F., Pairs of recursive structures. Annals of Pure and Applied Logic, vol. 46 (1990), no. 3, pp. 211–234.Google Scholar
Chong, Chi Tat and Wang, Wei, Hyperimmune-free degrees beyond ω, in preparation.Google Scholar
Downey, Rodney G. and Knight, Julia F., Orderings with αth jump degree 0(α). Proceedings of the American Mathematical Society, vol. 114 (1992), no. 2, pp. 545–552.Google Scholar
Downey, Rodney G., Lempp, Steffen, and Wu, Guohua, On the complexity of the successivity relation in computable linear orderings. Journal of Mathematical Logic, vol. 10 (2010), vol. 1–2, pp. 83–99.Google Scholar
Downey, Rodney G. and Moses, Michael F., Recursive linear orders with incomplete successivities. Transactions of the American Mathematical Society, vol. 326 (1991), no. 2, pp. 653–668.Google Scholar
Frolov, Andrey N., Presentations of the adjacency relation of a computable linear order. Izvestiya Vysshikh Uchebnykh Zavedenii. Matematika, vol. 7 (2010), pp. 64–74.Google Scholar
Frolov, Andrey N., Kalimullin, Iskander Sh., Harizanov, Valentina S., Kudinov, Oleg V., and Miller, Russell G., Spectra of high nand non-low ndegrees. Journal of Logic and Computation, vol. 22 (2012), no. 4, pp. 755–777.Google Scholar
Goncharov, Sergey S., Harizanov, Valentina S., Knight, Julia F., McCoy, Charles F. D., Miller, Russell G., and Reed Solomon, D., Enumerations in computable structure theory. Annals of Pure and Applied logic, vol. 136 (2005), no. 3, pp. 219–246.CrossRefGoogle Scholar
Greenberg, Noam, Kach, Asher M., Lempp, Steffen, and Turetsky, Daniel D., Computability and uncountable linear orders, part I: computable categoricity, this Journal, vol. 80 (2015), no. 1, pp. 116–144.Google Scholar
Greenberg, Noam and Knight, Julia F., Computable structure theory using admissible recursion theory on ω 1, Effective mathematics of the uncountable (Greenberg, Hirschfeldt, Miller, Hamkins, editors), Lecture Notes in Logic, Association for Symbolic Logic and Cambridge University Press, pp. 50–80, 2013, to appear.Google Scholar
Jockusch, Carl G. Jr. and Soare, Robert I., Degrees of orderings not isomorphic to recursive linear orderings. Annals of Pure and Applied Logic, vol. 52 (1991), no. 1-2, 39–64. International Symposium on Mathematical Logic and its Applications (Nagoya, 1988).Google Scholar
Knight, Julia F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), no. 4, pp. 1034–1042.Google Scholar
Miller, Russell G., The ${\rm{\Delta }}_2^0 $-spectrum of a linear order, this Journal, vol. 66 (2001), no. 2, pp. 470–486.Google Scholar
Moses, Michael F., Recursive linear orders with recursive successivities. Annals of Pure and Applied Logic, vol. 27 (1984), no. 3, pp. 253–264.Google Scholar
Gordon Rice, H., Recursive and recursively enumerable orders. Transactions of the American Mathematical Society, vol. 83 (1956), pp. 277–300.Google Scholar
Richter, Linda Jean, Degrees of structures, this Journal, vol. 46 (1981), no. 4, pp. 723–731.Google Scholar
Sacks, Gerald E., Higher recursion theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.Google Scholar
Takeuti, Gaisi, On the recursive functions of ordinal numbers. Journal of the Mathematical Society of Japan, vol. 12 (1960), pp. 119–128.Google Scholar
Uspenskii, Vladimir A., Some notes on recursively enumerable sets. Zeitschrift fur mathematische Logik und Grundlagen der Mathematik, vol. 3 (1957), pp. 157–170.Google Scholar
Wehner, Stephan, Enumerations, countable structures and Turing degrees. Proceedings of the American Mathematical Society, vol. 126 (1998), no. 7, pp. 2131–2139.Google Scholar