Hostname: page-component-5cf477f64f-tx7qf Total loading time: 0 Render date: 2025-04-07T01:35:38.029Z Has data issue: false hasContentIssue false
  • English
  • Français

THE COMPLEXITY OF ORDER-COMPUTABLE SETS

Part of: Computability and recursion theory Theory of computing

Published online by Cambridge University Press:  24 January 2025

HUISHAN WU
HUISHAN WU*
Affiliation:
SCHOOL OF INFORMATION SCIENCE BEIJING LANGUAGE AND CULTURE UNIVERSITY 15 XUEYUAN ROAD, HAIDIAN DISTRICT BEIJING 100083 CHINA
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper studies the conjecture of Hirschfeldt, Miller, and Podzorov in [13] on the complexity of order-computable sets, where a set A is order-computable if there is a computable copy of the structure 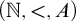$(\mathbb {N}, <,A)$ in the language of linear orders together with a unary predicate. The class of order-computable sets forms a subclass of 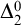$\Delta ^{0}_{2}$ sets. Firstly, we study the complexity of computably enumerable (c.e.) order-computable sets and prove that the index set of c.e. order-computable sets is 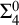$\Sigma ^{0}_{4}$-complete. Secondly, as a corollary of the main result on c.e. order-computable sets, we obtain that the index set of general order computable sets is 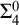$\Sigma ^{0}_{4}$-complete within the index set of 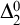$\Delta ^{0}_{2}$ sets. Finally, we continue to study the complexity of more general 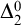$\Delta ^{0}_{2}$ sets and prove that the index set of 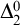$\Delta ^{0}_{2}$ sets is 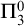$\Pi ^{0}_{3}$-complete.

Keywords

computability theoryorder-computable setsΔ02 sets

MSC classification

Primary: 03D80: Applications of computability and recursion theory 68Q15: Complexity classes (hierarchies, relations among complexity classes, etc.) 68Q17: Computational difficulty of problems (lower bounds, completeness, difficulty of approximation, etc.)
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 24
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ash, C. J. and Knight, J. F., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, 144, North-Holland Publishing Co., Amsterdam, 2000.Google Scholar
Calvert, W., The isomorphism problem for classes of computable fields . Archive for Mathematical Logic, vol. 43 (2004), pp. 327–336.Google Scholar
Calvert, W., The isomorphism problem for computable Abelian $p$ -groups of bounded length . Journal of Symbolic Logic, vol. 70 (2005), pp. 331–345.Google Scholar
Calvert, W. and Knight, J. F., Classification from a computable viewpoint . The Bulletin of Symbolic Logic, vol. 12 (2006), pp. 191–218.Google Scholar
Conidis, C. J., On the complexity of radicals in noncommutative rings . Journal of Algebra, vol. 322 (2009), pp. 3670–3680.Google Scholar
Conidis, C. J., The complexity of module radicals . Notre Dame Journal of Formal Logic, vol. 62 (2021), pp. 353–368.Google Scholar
Downey, R. G. and Hirschfeldt, D. R., Computability theory , Algorithmic Randomness and Complexity, Theory and Applications of Computability, (L. Bienvenu, P. Bonizzoni, V. Brattka, E. Mayordomo, and P. Panangaden, editors), Springer, New York, NY, 2010, pp. 7–109.Google Scholar
Downey, R. G. and Melnikov, A. G., Effectively categorical abelian groups . Journal of Algebra, vol. 373 (2013), pp. 223–248.Google Scholar
Downey, R. G. and Melnikov, A. G., Computable completely decomposable groups . Transactions of the American Mathematical Society, vol. 366 (2014), pp. 4243–4266.Google Scholar
Downey, R. G. and Montalbán, A., The isomorphism problem for torsion-free abelian groups is analytic complete . Journal of Algebra, vol. 320 (2008), pp. 2291–2300.Google Scholar
Harizanov, V. S., Pure computable model theory , Handbook of Recursive Mathematics: Recursive Model Theory, vol. 1, (Ershov, Yu. L., Goncharov, S. S., Nerode, A., Remmel, J. B., and Marek, V. W., editors), volume 138 of Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 1998, pp. 3–114.Google Scholar
Harizanov, V. S., Lempp, S., McCoy, C. F. D., Morozov, A. S., and Solomon, R., On the isomorphism problem for some classes of computable algebraic structures . Archive for Mathematical Logic, vol. 61 (2022), pp. 813–825.Google Scholar
Hirschfeldt, D., Miller, R., and Podzorov, S., Order-computable sets . Notre Dame Journal of Formal Logic, vol. 48 (2007), pp. 317–347.Google Scholar
Lempp, S., The computational complexity of torsion-freeness of finitely presented groups . Bulletin of the Australian Mathematical Society, vol. 56 (1997), pp. 273–277.Google Scholar
Melnikov, A. G., Computable abelian groups . Bulletin of Symbolic Logic, vol. 20 (2014), pp. 315–356.Google Scholar
Nies, A., Computability and Randomness, Oxford University Press, Inc., New York, 2009.Google Scholar
Riggs, K., The decomposablity problem for torsion-free abelian groups is analytic-complete . Proceedings of the American Mathmatical Society, vol. 143 (2015), pp. 3631–3640.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees, Springer-Verlag, Berlin, 1987.Google Scholar
Soare, R. I., Turing Computability, Springer-Verlag, Berlin, Heidelberg, 2016.Google Scholar
Wu, H., The complexity of decomposability of computable rings . Notre Dame Journal of Formal Logic, vol. 64 (2023), pp. 1–14.Google Scholar