Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Durand, Bruno
Romashchenko, Andrei
and
Shen, Alexander
2008.
Developments in Language Theory.
Vol. 5257,
Issue. ,
p.
276.
Durand, Bruno
Romashchenko, Andrei
and
Shen, Alexander
2009.
Automata, Languages and Programming.
Vol. 5555,
Issue. ,
p.
403.
Durand, Bruno
and
Poupet, Victor
2009.
Developments in Language Theory.
Vol. 5583,
Issue. ,
p.
195.
Durand, Bruno
Romashchenko, Andrei
and
Shen, Alexander
2010.
Fields of Logic and Computation.
Vol. 6300,
Issue. ,
p.
208.
Jeandel, Emmanuel
and
Vanier, Pascal
2011.
Theory and Applications of Models of Computation.
Vol. 6648,
Issue. ,
p.
230.
Shen, Alexander
2011.
Computer Science – Theory and Applications.
Vol. 6651,
Issue. ,
p.
105.
Durand, Bruno
Romashchenko, Andrei
and
Shen, Alexander
2012.
Fixed-point tile sets and their applications.
Journal of Computer and System Sciences,
Vol. 78,
Issue. 3,
p.
731.
Jeandel, Emmanuel
and
Vanier, Pascal
2013.
Turing degrees of multidimensional SFTs.
Theoretical Computer Science,
Vol. 505,
Issue. ,
p.
81.
Levin, Leonid A.
2013.
Forbidden information.
Journal of the ACM,
Vol. 60,
Issue. 2,
p.
1.
Khan, Mushfeq
2013.
Shift-complex sequences.
The Bulletin of Symbolic Logic,
Vol. 19,
Issue. 2,
p.
199.
Durand, Bruno
Gamard, Guilhem
and
Grandjean, Anaël
2014.
Developments in Language Theory.
Vol. 8633,
Issue. ,
p.
166.
Durand, Bruno
and
Romashchenko, Andrei
2015.
Mathematical Foundations of Computer Science 2015.
Vol. 9234,
Issue. ,
p.
218.
Saltzman, Peter
2015.
Architecture and Mathematics from Antiquity to the Future.
p.
585.
BIENVENU, LAURENT
and
PORTER, CHRISTOPHER P.
2016.
DEEP CLASSES.
The Bulletin of Symbolic Logic,
Vol. 22,
Issue. 2,
p.
249.
Westrick, Linda Brown
2017.
Seas of squares with sizes from a Π
1
0
set.
Israel Journal of Mathematics,
Vol. 222,
Issue. 1,
p.
431.
Durand, Bruno
Gamard, Guilhem
and
Grandjean, Anaël
2017.
Aperiodic tilings and entropy.
Theoretical Computer Science,
Vol. 666,
Issue. ,
p.
36.
Downey, Rod
and
Hirschfeldt, Denis R.
2019.
Algorithmic randomness.
Communications of the ACM,
Vol. 62,
Issue. 5,
p.
70.
Ng, Tim
Ochem, Pascal
Rampersad, Narad
and
Shallit, Jeffrey
2019.
Combinatorics on Words.
Vol. 11682,
Issue. ,
p.
264.
Törmä, Ilkka
2020.
Countable Sofic Shifts with a Periodic Direction.
Theory of Computing Systems,
Vol. 64,
Issue. 6,
p.
1042.
DURAND, BRUNO
and
ROMASHCHENKO, ANDREI
2021.
The expressiveness of quasiperiodic and minimal shifts of finite type.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 4,
p.
1086.


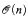 Kolmogorov complexity of its (
Kolmogorov complexity of its (