The aim of the paper is to prove the completeness theorem for biprobability models. This also solves Keisler's Problem 5.4 (see [4]).

Let 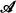be a countable admissible set and ω ∈ 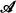. The logic 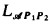is similar to the standard probability logic 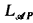. The only difference is that two types of probability quantifiers 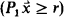and 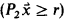are allowed.

A biprobability model is a structure (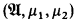, μ1, μ2) where 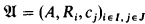is a classical structure without operations and μ1, μ2 are two types of probability measures such that μ1 is absolutely continuous with respect to μ2, i.e. μ1 ≪ μ2.

The quantifiers are interpreted in the natural way, i.e.

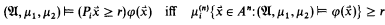
for i = 1, 2. (The measure 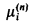is the restriction of the completion of 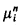to the σ-algebra generated by the measurable rectangles and the diagonal sets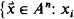

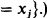
Axioms and rules of inference are those of 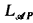, as listed in [2] with the axiom B4 from [4], with the remark that both P1 and P2 can play the role of P, together with the following axioms:

Axioms of continuity.

• 1) .

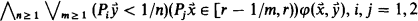• 2) .

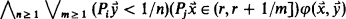Axiom of absolute continuity:

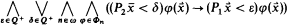
where 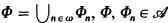and Φn = {φ ∈ Φ: φ has n free variables}.