Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-20T03:36:43.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Complete theories with only universal and existential axioms

Published online by Cambridge University Press:  12 March 2014

A. H. Lachlan
A. H. Lachlan*
Affiliation:
Department of Mathematics and Statistics, Simon Fraser University, Burnaby, British Columbia V5A 1S6, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

Let T be a complete first-order theory over a finite relational language which is axiomatized by universal and existential sentences. It is shown that T is almost trivial in the sense that the universe of any model of T can be written 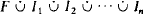. where F is finite and I 1, I 2, …, In are mutually indiscernible over F. Some results about complete theories with ∃∀-axioms over a finite relational language are also mentioned.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 3 , September 1987 , pp. 698 - 711
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Hodkinson, I. M. and Macpherson, H. D., Relational structures determined by their finite induced substructures, this Journal (to appear).Google Scholar
[2] Macpherson, H. D., Graphs determined by their finite induced subgraphs, Journal of Combinatorial Theory, Series B, vol. 41 (1986), pp. 230–234.CrossRefGoogle Scholar
[3] Pouzet, M., Application d'une propriété combinatoire des parties d'un ensemble aux groupes et aux relations, Mathematische Zeitschrift, vol. 150 (1976), pp. 117–134.CrossRefGoogle Scholar
[4] Shelah, S., Classification theory and the number of non-isomorphic models, North-Holland, Amsterdam, 1978.Google Scholar