Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-22T20:28:02.964Z Has data issue: false hasContentIssue false
  • English
  • Français

A complete, decidable theory with two decidable models1

Published online by Cambridge University Press:  12 March 2014

Terrence S. Millar
Terrence S. Millar*
Affiliation:
Kantor Pos, Watansoppeng, Selawesi Selatan, Indonesia
Get access Rights & Permissions [Opens in a new window]

Extract

A well-known result of Vaught's is that no complete theory has exactly two nonisomorphic countable models. The main result of this paper is that there is a complete decidable theory with exactly two nonisomorphic decidable models.

A model is decidable if it has a decidable satisfaction predicate. To be more precise, let T be a decidable theory, let {θn∣n < ω} be an effective enumeration of all formulas in L(T), and let 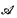be a countable model of T. For any indexing E = {ai∣ i < ω} of ∣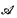∣, and any formula ϕ ∈ L(T), let ‘ϕE’ denote the result of substituting ‘ai’ for every free occurrence of ‘xi’ in ϕ, i < ω. Then 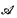is decidable just in case, for some indexing E of ∣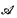∣, {n ∣ 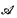⊨ θnE} is a recursive set of integers. It is easy to show that the decidability of a model does not depend on the choice of the effective enumeration of the formulas in L(T); we omit details. By a simple ‘effectivization’ of Henkin's proof of the completeness theorem (see Chang [1]) we have

Fact 1. Every decidable consistent theory has a decidable model.

Assume next that T is a complete decidable theory and {θn ∣ n < ω} is an effective enumeration of all formulas of L(T).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 3 , September 1979 , pp. 307 - 312
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The author thanks the referee for a suggestion that considerably shortened the proof of the main theorem of this article.

References

BIBLIOGRAPHY

[1]Chang, C. C. and Keisler, H. J., Model theory, American Elsevier, New York, 1973.Google Scholar
[2]Harrington, L., Recursively presentable prime models, this Journal, vol. 39(1974), pp. 305–309.Google Scholar
[3]Metakides, G. and Nerode, A., Recursion theory and algebra, Algebra and logic, Lecture Notes in Mathematics, no. 450, Springer-Verlag, Berlin and New York, 1975, pp. 209–219.CrossRefGoogle Scholar
[4]Millar, T. S., Foundations of recursive model theory, Annals of Mathematical Logic, vol. 13(1978), pp. 45–72.CrossRefGoogle Scholar
[5]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[6]Sacks, G. E., Saturated model theory, Benjamin, Reading, Massachusettes, 1972.Google Scholar