Article contents
A COMPARISON OF VARIOUS ANALYTIC CHOICE PRINCIPLES
Published online by Cambridge University Press: 08 June 2021
Abstract
We investigate computability theoretic and descriptive set theoretic contents of various kinds of analytic choice principles by performing a detailed analysis of the Medvedev lattice of 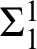 $\Sigma ^1_1$
-closed sets. Among others, we solve an open problem on the Weihrauch degree of the parallelization of the
$\Sigma ^1_1$
-closed sets. Among others, we solve an open problem on the Weihrauch degree of the parallelization of the 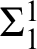 $\Sigma ^1_1$
-choice principle on the integers. Harrington’s unpublished result on a jump hierarchy along a pseudo-well-ordering plays a key role in solving this problem.
$\Sigma ^1_1$
-choice principle on the integers. Harrington’s unpublished result on a jump hierarchy along a pseudo-well-ordering plays a key role in solving this problem.
MSC classification
- Type
- Article
- Information
- Copyright
- © Association for Symbolic Logic 2021
References
- 4
- Cited by



