Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-09T14:44:17.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Colimit completions and the effective topos

Published online by Cambridge University Press:  12 March 2014

Edmund Robinson  and
Giuseppe Rosolini
Edmund Robinson*
Affiliation:
Department of Computing and Information Science, Queen's University, Kingston, Ontario K7L 3N6, Canada
Giuseppe Rosolini
Affiliation:
Dipartimento Di Matematica, Università Di Parma, 43100 Parma, Italy
*
School of Cognitive and Computing Sciences, University of Sussex, Brighton BN1 9QH, England
Get access Rights & Permissions [Opens in a new window]

Extract

The family of readability toposes, of which the effective topos is the best known, was discovered by Martin Hyland in the late 1970's. Since then these toposes have been used for several purposes. The effective topos itself was originally intended as a category in which various recursion-theoretic or effective constructions would live as natural parts of the higher-order type structure. For example the hereditary effective operators become the higher types over N (Hyland [1982]), and effective domains become the countably-based domains in the topos (McCarty [1984], Rosolini [1986]). However, following the discovery by Moggi and Hyland that it contained nontrivial small complete categories, the effective topos has also been used to provide natural models of polymorphic type theories, up to and including the theory of constructions (Hyland [1987], Hyland, Robinson and Rosolini [1987], Scedrov [1987], Bainbridge et al. [1987]).

Over the years there have also been several different constructions of the topos. The original approach, as in Hyland [1982], was to construct the topos by first giving a notion of Pω-valued set. A Pω-valued set is a set X together with a function =x: X × X → Pω. The elements of X are to be thought of as codes, or as expressions denoting elements of some “real underlying” set in the topos. Given a pair (x,x′) of elements of X, the set =x (x,x′) (generally written 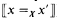) is the set of codes of proofs that the element denoted by x is equal to the element denoted by x′.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 55 , Issue 2 , June 1990 , pp. 678 - 699
Copyright
Copyright © Association for Symbolic Logic 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bainbridge, E. S., Freyd, P. J., Scedrov, A. and Scott, P. J. [1987], Functorial polymorphism, Logical foundations of functional programming (proceedings, Austin, Texas, 1987; Huet, G., editor), Addison-Wesley, Reading, Massachusetts (to appear).Google Scholar
Barr, M. [1971], Exact categories, Exact categories and categories of sheaves (Barr, M.et al., editors), Lecture Notes in Mathematics, vol. 236, Springer-Verlag, Berlin, pp. 1–120.CrossRefGoogle Scholar
Bénabou, J. [1985], Foundations of category theory, this Journal, vol. 50, pp. 10–37.Google Scholar
Carboni, A. and Magno, R. Celia [1982], The free exact category on a left exact one, Journal of the Australian Mathematical Society, Series A, vol. 33, pp. 295–301.CrossRefGoogle Scholar
Carboni, A., Freyd, P. J. and Scedrov, A. [1987], A categorical approach to realizability and polymorphic types, Mathematical foundations of programming language semantics (proceedings, New Orleans, Louisiana, 1987; Main, M. G.et al., editors), Lecture Notes in Computer Science, vol. 298, Springer-Verlag, Berlin, 1988, pp. 23–42.Google Scholar
Freyd, P. J. [1987], The realizability universe, Lectures at the Montreal category seminar, 10 10–11, 1987.Google Scholar
Gabriel, P. and Zisman, M. [1967], Calculus of fractions andhomotopy theory, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Hyland, J. M. E. [1982], The effective topos, The L. E. J. Brouwer centenary symposium (Troelstra, A. S. and van Dalen, D., editors), North-Holland, Amsterdam, pp. 165–216.Google Scholar
Hyland, J. M. E.[1987], A small complete category, Proceedings of the conference on Church's thesis: fifty years later (to appear).Google Scholar
Hyland, J. M. E., Johnstone, P. T. and Pitts, A. M. [1980], Tripos theory, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 88, pp. 205–232.CrossRefGoogle Scholar
Hyland, J. M. E., Robinson, E. P. and Rosolini, G. [1987], The discrete objects in the effective topos (to appear).Google Scholar
Kleene, S. C. [1945], On the interpretation of intuitionistic number theory, this Journal, vol. 10, pp. 109–124.Google Scholar
Lane, S. Mac [1971], Categories for the working mathematician, Springer-Verlag, Berlin.CrossRefGoogle Scholar
McCarty, D. C. [1984], Realizability and recursive mathematics, D. Phil, thesis, Oxford University, Oxford.Google Scholar
Mulry, P. J. [1981], Generalized Banach-Mazw functionals in the topos of recursive sets, Journal of Pure and Applied Algebra, vol. 26, pp. 71–83.CrossRefGoogle Scholar
Rosolini, G. [1986], Continuity and effectiveness in topoi, D. Phil, thesis, Oxford University, Oxford; published as Technical Report CMU-CS-86-123, Department of Computer Science, Carnegie-Mellon University, Pittsburgh, Pennsylvania.Google Scholar
Scedrov, A. [1987], HEO semantics for a calculus of constructions (to appear).Google Scholar
Scott, D. S. [1979], Identity and existence in intuitionistic logic, Applications of sheaves (Fourman, M. P.et al., editors), Lecture Notes in Mathematics, vol. 753, Springer-Verlag, Berlin, pp. 660–696.CrossRefGoogle Scholar
Troelstra, A. S. [1973], Metamathematical investigation of intuitionistic arithmetic and analysis, Lecture Notes in Mathematics, vol. 344, Springer-Verlag, Berlin.CrossRefGoogle Scholar