Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T06:06:49.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherence and the axioms of confirmation1

Published online by Cambridge University Press:  12 March 2014

Abner Shimony
Abner Shimony*
Affiliation:
Neptune, New Jersey
Get access Rights & Permissions [Opens in a new window]

Extract

It has been pointed out by Carnap that ‘probability’ is an equivocal term, which is used currently in two senses: (i) the degree to which it is rational to believe a hypothesis h on specified evidence e, and (ii) the relative frequency (in an indefinitely long run) of one property of events or things with respect to another. This paper is concerned only with the first of these two senses, which will be referred to as ‘the concept of confirmation,’ in order to avoid equivocation.

We may distinguish a quantitative and a comparative concept of confirmation. The general form of statements involving the former is

The degree of confirmation of the proposition h, given the proposition

e as evidence, is r (where r is a real number between 0 and 1).

In this paper the notation for a statement of this form is

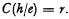
The general form of statements involving the comparative concept is The proposition h is equally or less confirmed on e than is the proposition h′ on e′,

which may be symbolized as

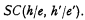
The following abbreviations will also be used in discussing comparative confirmation:

The former of these two abbreviations means intuitively

The proposition h is less confirmed on evidence e than h′ is on e′. The latter means

The proposition h is confirmed on evidence e to the same degree that h′ is on e′.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 20 , Issue 1 , March 1955 , pp. 1 - 28
Copyright
Copyright © Association for Symbolic Logic 1955

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

From a dissertation in partial fulfillment of the requirements for the degree of Ph. D. in the Department of Philosophy of Yale University, and written in part while the author was a Sterling Fellow in 1951–52. I am grateful to Professors Rudolf Carnap, John Myhill, John Kemeny, Frederic Fitch, and Howard Stein for their very helpful suggestions on the material in this paper.

References

2 Logical foundations of probability, Chicago, 1950, pp. 23–26Google Scholar.

3 R. Carnap, op. cit., p. 431.

4 Koopman, B. O., The axioms and algebra of intuitive probability, Annals of mathematics, Series 2, vol. 41 (1940), pp. 269–292CrossRefGoogle Scholar.

5 von Kries, J., Die Prinzipien der Wahrscheinlichkeitsrechnung. Eine logische Untersuchung, Freiburg i.B., 1886, pp. 29 ffGoogle Scholar; Keynes, J. M., A treatise on probability, London and New York, 1921, ch. IIIGoogle Scholar.

6 Theory of probability (second edition), Oxford, 1948, pp. 17–25Google Scholar.

7 Zur Axiomatik der Wahrscheinlichkeitsrechnung, Comptes rendus de la Société des Sciences de Varsovie, C1. III, xxv (1932), pp. 1–4Google Scholar.

8 On confirmation, this Journal, vol. 5 (1940), pp. 133–148Google Scholar. Induction et analogie: comparaison de leur fondement, Mind, vol. 50 (1941), pp. 351–365Google Scholar.

9 The logical problem of induction, Helsingfors, 1941, pp. 106–7Google ScholarPubMed.

10 Op. cit., p. 285.

11 Probability and induction, Oxford, 1949, pp. 125–27Google ScholarPubMed.

12 For a comparison of some of these axiomatizations see section 62 of Carnap's Logical foundations of probability. It should be particularly noted that the arguments h, e of the function C in the above set of axioms are propositions rather than sentences. Consequently, the modal operator ‘⥽’ is used rather than the corresponding metalinguistic operator; likewise the modal operator will be used in subsequent discussions, ‘◊p’ means ‘p is possible’, and ‘p ⥽q’ means ‘p logically implies q’ but for a detailed discussion of these operators see Fitch, F. B., Symbolic logic: an introduction, especially p. 66 and p. 71Google Scholar. The assumption made at the beginning of this paper that all evidential propositions are logically possible makes it superfluous to write explicitly the propositions ‘◊e’ ‘◊(h&c)’ and ’◊(h′&e)’ as antecedents to the above axioms. Finally it should be noted that in subsequent discussions I shall consider a stronger set of axioms in which (2) is replaced by the following (2′) : C(h/e) = 1 if and only if e ⥽ h.

13 See section 5 of this paper.

14 Hosiasson-Lindonbaum, J., Induction et analogie: comparaison de leur fondement, Mind, vol. 50 (1941), p. 353Google Scholar.

15 Kemeny, J., Carnap on confirmation, The review of metaphysics, vol. 5 (1941), pp. 152–53Google Scholar.

16 Poincaré, , Calcul des probabilités (second edition), Paris, 1912, pp. 37–9Google Scholar; Kneale, W., Probability and induction, pp. 125–27Google Scholar.

17 On some aspects of the theory of probability, Philosophical magazine, 6th series, vol. 38 (1919), pp. 715–731, especially, p. 722CrossRefGoogle Scholar.

18 Op. cit., pp. 135–38.

19 Op. cit., pp. 275–76.

20 Probability, frequency, and reasonable expectation, American journal of physics, vol. 14 (1946), pp. 1–13CrossRefGoogle Scholar.

21 Ramsey, F. P., Truth and probability, The foundations of mathematics and other logical essays, London and New York, 1931Google Scholar; DeFinetti, B., Sul significato soggetivo della probabilità, Fundamenta mathematicae, vol. 17 (1931), pp. 298–329Google Scholar, and La prévision: ses lois logiques, ses sources subjectives, Annales de l'Institut Henri Poincaré, vol. 7 (1937), pp. 1–68Google Scholar.

22 R. Carnap, op. cit., section 51.

23 La prévision: ses lois logiques, ses sources subjectives, Annales de l'Institut Henri Poincaré, vol. 7 (1937), p. 7Google Scholar.

24 Op. cit., pp. 182–83.

25 R. Carnap, op. cit., pp. 83–84.

26 Gödel, K., Russell's mathematical logic, The philosophy of Bertrand Russell (edited by Schilpp, P. A.), Menasha, Wisconsin, 1946, pp. 150–52Google Scholar.

27 Op. cit., p. 150.

28 K. Gödel, op. cit., pp. 150–52; also his What is Cantor's continuum hypothesis, American mathematical monthly, vol. 54 (1947), pp. 520–22Google Scholar.

29 The difficulty of extending the notion of coherence so as to apply to infinite sets will be pointed out in § 5.

30 If this condition is satisfied we shall often use the expression ‘(h, e) and (h′, e′) are comparable’.

31 However, the assumption has been made that ‘C(h/e)’ and ‘SC(h/e, h′/e′)’ axe well-defined only if e and e′ are logically possible propositions.

32 Fair beis and inductive probabilities, (unpublished manuscript).

33 Kemeny also proved the following : a sufficient condition for C to be such that every finite set of quantitative beliefs regulated by C is coherent in the usual sense of Ramsey and DeFinetti is that C should satisfy axioms (1), (2), (3), and (4).

34 Kolmogoroff, A., The foundations of probability, New York, 1950, p. 15Google Scholar.

35 Cf. footnote 19.

36 ‘p ≣ q’ means ‘p is logically or strictly equivalent to q.’ See F. B. Fitch, op. cit., pp. 77–78.

37 Op. cit., footnote 4.

38 Cf. the discussion of weight measurements in Cohen, M. and Nagel, E., An introduction to logic and scientific method, New York, 1934, pp. 297–8Google Scholar.

39 B. O. Koopman, op. cit., pp. 290–91, especially theorems 20, 24, 25.

40 The bases of probability, Bulletin of the American Mathematical Society, vol. 46 (1940), p. 769Google Scholar.

41 For a discussion of this principle, see J. M. Keynes, op. cit., pp. 41–64. In my dissertation, A theory of confirmation (submitted to the Graduate School of Yale University in 1953), I attempted to establish the analyticity of a strict formulation of the principle.

42 Op. cit., pp. 29 ff.

43 Op. cit., pp. 34–40.

44 Sur l'extension de l'ordre partiel, Fundamenta mathematicae, vol. 16 (1930), pp. 386–89CrossRefGoogle Scholar. This theorem was independently proved by Professor E. Begle of the Department of Mathematics of Yale University.

45 Prolegomena to any future metaphysics, translated by Carus, Paul, Chicago, 1912, section 36Google Scholar.

46 A system of logic, BK. III, ch. III.

47 Op. cit., chapters xx–xxii.

48 Op. cit., p. 113.