Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T08:41:39.882Z Has data issue: false hasContentIssue false
  • English
  • Français

Codable sets and orbits of computably enumerable sets

Published online by Cambridge University Press:  12 March 2014

Leo Harrington  and
Robert I. Soare
Leo Harrington
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, USA, E-mail: [email protected]
Robert I. Soare
Affiliation:
Department of Mathematics, University of Chicago, 5734 University Avenue, Chicago, IL 60637, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A set X of nonnegative integers is computably enumerable (c.e.), also called recursively enumerable (r.e.), if there is a computable method to list its elements. Let ε denote the structure of the computably enumerable sets under inclusion, ε = ({We}eϵω,⊆). We previously exhibited a first order ε-definable property Q(X) such that Q(X) guarantees that X is not Turing complete (i.e., does not code complete information about c.e. sets).

Here we show first that Q(X) implies that X has a certain “slowness” property whereby the elements must enter X slowly (under a certain precise complexity measure of speed of computation) even though X may have high information content. Second we prove that every X with this slowness property is computable in some member of any nontrivial orbit, namely for any noncomputable A ϵ ε there exists B in the orbit of A such that X ≤TB under relative Turing computability (≤T). We produce B using the 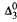-automorphism method we introduced earlier.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 1 , March 1998 , pp. 1 - 28
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ambos-Spies, K., Jockusch, C. G. Jr., Shore, R. A., and Soare, R. I., An algebraic decomposition of the recursively enumerable degrees and the coincidence of several degree classes with the promptly simple degrees, Transactions of the American Mathematical Society, vol. 281 (1984), pp. 109–128.CrossRefGoogle Scholar
[2]Cholak, P. A., Automorphisms of the lattice of recursively enumerable sets, Memoirs of the American Mathematical Society, vol. 113 (1995).CrossRefGoogle Scholar
[3]Harrington, L. and Soare, R. I., Definable properties of the computably enumerable sets, Proceedings of the 1996 Oberwolfach conference on computability theory (Ambos-Spies, K., Slaman, T., and Soare, R., editors), to appear in Journal of Pure and Applied Logic.Google Scholar
[4]Harrington, L. and Soare, R. I., Martin's invariance conjecture and low sets, in preparation.Google Scholar
[5]Harrington, L. and Soare, R. I., Post's program and incomplete recursively enumerable sets, Proceedings of the National Academy of Sciences of the United States of America, vol. 88 (1991), pp. 10242–10246.CrossRefGoogle ScholarPubMed
[6]Harrington, L. and Soare, R. I., Dynamic properties of computably enumerable sets, Computability, enumerability, unsolvability: Directions in recursion theory, proceedings of the recursion theory conference, University of Leeds, July, 1994 (Cooper, S. B., Slaman, T. A., and Wainer, S. S., editors), London Mathematical Society Lecture Notes Series, Cambridge University Press, 01 1996.Google Scholar
[7]Harrington, L. and Soare, R. I., The -automorphism method and noninvariant classes of degrees, Journal of the American Mathematical Society, vol. 9 (1996), pp. 284–321.CrossRefGoogle Scholar
[8]Lachlan, A. H., Degrees of recursively enumerable sets which have no maximal superset, this Journal, vol. 33 (1968), pp. 431–443.Google Scholar
[9]Lachlan, A. H., The elementary theory of recursively enumerable sets, Duke Mathematics Journal, vol. 35 (1968), pp. 123–146.CrossRefGoogle Scholar
[10]Lachlan, A. H., On some games which are relevant to the theory of recursively enumerable sets, Annals of Mathematics. Second Series, vol. 91 (1970), pp. 291–310.CrossRefGoogle Scholar
[11]Lerman, M. and Soare, R. I., d-simple sets, small sets, and degree classes, Pacific Journal of Mathematics, vol. 87 (1980), pp. 135–155.CrossRefGoogle Scholar
[12]Maass, W., Recursively enumerable generic sets, this Journal, vol. 47 (1982), pp. 809–823.Google Scholar
[13]Maass, W., Variations on promptly simple sets, this Journal, vol. 50 (1985), pp. 138–148.Google Scholar
[14]Maass, W., Shore, R. A., and Stob, M., Splitting properties and jump classes, Israel Journal of Mathematics, vol. 39 (1981), pp. 210–224.CrossRefGoogle Scholar
[15]Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Z. Math. Logik Grundlag. Math., vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar
[16]Post, E. L., Recursively enumerable sets of positive integers and their decision problems, Bulletin of the American Mathematical Society, vol. 50 (1944), pp. 284–316.CrossRefGoogle Scholar
[17]Shoenfield, J. R., Degrees of classes of r.e. sets, this Journal, vol. 41 (1976), pp. 695–696.Google Scholar
[18]Soare, R. I., Automorphisms of the recursively enumerable sets, part I: Maximal sets, Annals of Mathematics. Second Series, vol. 100 (1974), pp. 80–120.CrossRefGoogle Scholar
[19]Soare, R. I., Recursively enumerable sets and degrees: A study of computable functions and computably generated sets, Springer-Verlag, Heidelberg, 1987.CrossRefGoogle Scholar
[20]Soare, R. I., Computability and recursion, Bulletin of Symbolic Logic, vol. 2 (1996), to appear.CrossRefGoogle Scholar
[21]Turing, A. M., Systems of logic based on ordinals, Proceedings of the London Mathematical Society, vol. 45 (1939), pp. 161–228, reprinted in Davis [1965], pp. 154–222.CrossRefGoogle Scholar