No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
Probably the two most famous examples of elementary embeddings between inner models of set theory are the embeddings of the universe into an inner model given by a measurable cardinal and the embeddings of the constructible universe L into itself given by 0#. In both of these examples, the “target model” is a subclass of the “ground model” (and in the latter case they are equal). It is not hard to find examples of embeddings in which the target model is not a subclass of the ground model: if 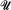 is a generic ultrafilter arising from forcing with a precipitous ideal on a successor cardinal κ, then the ultraproduct of the ground model via
is a generic ultrafilter arising from forcing with a precipitous ideal on a successor cardinal κ, then the ultraproduct of the ground model via 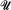 collapses κ. Such considerations suggest a classification of how close the target model comes to “fitting inside” the ground model.
collapses κ. Such considerations suggest a classification of how close the target model comes to “fitting inside” the ground model.
Definition 1.1. Let M and N be inner models (transitive, proper class models) of ZFC, and let j: M → N be an elementary embedding. The co-critical point of j is the least ordinal λ, if any exist, such that there is X ⊆ λ, X ∈ N but X ∉ M. Such an X is called a new subset of λ.
It is easy to see that the co-critical point of j: M → N is a cardinal in N.