Article contents
COARSE REDUCIBILITY AND ALGORITHMIC RANDOMNESS
Published online by Cambridge University Press: 12 August 2016
Abstract
A coarse description of a set A ⊆ ω is a set D ⊆ ω such that the symmetric difference of A and D has asymptotic density 0. We study the extent to which noncomputable information can be effectively recovered from all coarse descriptions of a given set A, especially when A is effectively random in some sense. We show that if A is 1-random and B is computable from every coarse description D of A, then B is K-trivial, which implies that if A is in fact weakly 2-random then B is computable. Our main tool is a kind of compactness theorem for cone-avoiding descriptions, which also allows us to prove the same result for 1-genericity in place of weak 2-randomness. In the other direction, we show that if 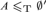 $A \le _{{\rm{T}}} \emptyset {\rm{'}}$ is a 1-random set, then there is a noncomputable c.e. set computable from every coarse description of A, but that not all K-trivial sets are computable from every coarse description of some 1-random set. We study both uniform and nonuniform notions of coarse reducibility. A set Y is uniformly coarsely reducible to X if there is a Turing functional Φ such that if D is a coarse description of X, then ΦD is a coarse description of Y. A set B is nonuniformly coarsely reducible to A if every coarse description of A computes a coarse description of B. We show that a certain natural embedding of the Turing degrees into the coarse degrees (both uniform and nonuniform) is not surjective. We also show that if two sets are mutually weakly 3-random, then their coarse degrees form a minimal pair, in both the uniform and nonuniform cases, but that the same is not true of every pair of relatively 2-random sets, at least in the nonuniform coarse degrees.
$A \le _{{\rm{T}}} \emptyset {\rm{'}}$ is a 1-random set, then there is a noncomputable c.e. set computable from every coarse description of A, but that not all K-trivial sets are computable from every coarse description of some 1-random set. We study both uniform and nonuniform notions of coarse reducibility. A set Y is uniformly coarsely reducible to X if there is a Turing functional Φ such that if D is a coarse description of X, then ΦD is a coarse description of Y. A set B is nonuniformly coarsely reducible to A if every coarse description of A computes a coarse description of B. We show that a certain natural embedding of the Turing degrees into the coarse degrees (both uniform and nonuniform) is not surjective. We also show that if two sets are mutually weakly 3-random, then their coarse degrees form a minimal pair, in both the uniform and nonuniform cases, but that the same is not true of every pair of relatively 2-random sets, at least in the nonuniform coarse degrees.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2016
References
REFERENCES
- 5
- Cited by


