We show that assuming modest large cardinals, there is a definable class of ordinals, closed and unbounded beneath every uncountable cardinal, so that for any closed and unbounded subclasses 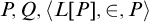$P, Q, {\langle L[P],\in ,P \rangle }$ and 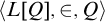${\langle L[Q],\in ,Q \rangle }$ possess the same reals, satisfy the Generalised Continuum Hypothesis, and moreover are elementarily equivalent. 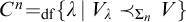Examples of such P are Card, the class of uncountable cardinals, I the uniform indiscernibles, or for any n the class $C^{n}{=_{{\operatorname {df}}}}\{ \lambda \, | \, V_{\lambda } \prec _{{\Sigma }_{n}}V\}$ ; moreover the theory of such models is invariant under ZFC-preserving extensions. They also all have a rich structure satisfying many of the usual combinatorial principles and a definable wellorder of the reals. The inner model constructed using definability in the language augmented by the Härtig quantifier is thus also characterized.