Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T23:21:28.881Z Has data issue: false hasContentIssue false
  • English
  • Français

The classification of excellent classes

Published online by Cambridge University Press:  12 March 2014

R. Grossberg  and
B. Hart
R. Grossberg
Affiliation:
Department of Mathematics, Rutgers University, New Brunswick, New Jersey 08903 Department of Mathematics, University of California, Berkeley, California 94720
Get access Rights & Permissions [Opens in a new window]

Extract

In [9] and [12], Shelah defined a certain type of Scott sentence which he called excellent. He proved, among other things, that if a Scott sentence is excellent and categorical in some uncountable power then it is categorical in all uncountable powers: the analog of the Morley categoricity theorem. Proving such an analog is often the starting point in the classification of a family of classes. Before beginning this classification in the case of excellent Scott sentences, let us say a few words about what this paper is and what it is not.

It is not the beginning of a classification theory for complete sentences in 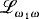where 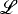is countable. Although excellence arises in the study of the model theory of Scott sentences, it is not a dividing line in a classification of them. In particular, the assumption of nonexcellence does not yield much information. In fact, in [3] there is an example of a nonexcellent Scott sentence, categorical in ℵ1 which is. not fully categorical. It seems to the second author that a classification of 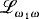sentences analogous to the classification of first order theories is a long way off and may not be accomplishable in ZFC.

This is not to say that the study of excellent Scott sentences (or the class of models of such which we will call excellent classes) is unproductive. Besides its extreme usefulness in [12], Mekler and Shelah have shown that excellence plays a decisive role in the study of almost free algebras (see [7]). Moreover, as the class of ω-saturated models of an ω-stable theory is an example of an excellent class, the study of excellent classes is at least as difficult as the study of first order ω-stable theories.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 4 , December 1989 , pp. 1359 - 1381
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Harrington, Leo and Makkai, Michael, An exposition of Shelah's main gap: counting uncountable models of ω-stable and superstable theories, Notre Dame Journal of Formal Logic, vol. 26 (1985), pp. 139–177.CrossRefGoogle Scholar
[2] Hart, Bradd, A proof of Morley's conjecture, this Journal, vol. 54 (1989), pp. 1346–1358.Google Scholar
[3] Hart, B. and Shelah, S., Categoricity over P for first order T or categoricity for can stop at ℵ k while holding for ℵ0,…, ℵ k−1 , Israel Journal of Mathematics (submitted).Google Scholar
[4] Hart, Bradd, Some results in classification theory, Ph.D. thesis, McGill University, Montréal, 1986.Google Scholar
[5] Hart, Bradd, An exposition of OTOP, Classification theory:proceedings, Chicago, 1985 (Baldwin, J. T., editor), Lecture Notes in Mathematics, vol. 1292, Springer-Verlag, Berlin, 1988, pp. 107–126.CrossRefGoogle Scholar
[6] Makkai, Michael, A survey of basic stability theory, with particular emphasis on orthogonality and regular types, Israel Journal of Mathematics, vol. 49 (1984), pp. 181–238.CrossRefGoogle Scholar
[7] Mekler, A. and Shelah, S., free algebras, Algebra Universalis (submitted).Google Scholar
[8] Shelah, Saharon, A combinatory problem; stability and order for models and theories in infinitary languages, Pacific Journal of Mathematics, vol. 41 (1972), pp. 247–261.CrossRefGoogle Scholar
[9] Shelah, Saharon, Categoricity in ℵ1, of sentences in , Israel Journal of Mathematics, vol. 20 (1975), pp. 127–148.CrossRefGoogle Scholar
[10] Shelah, Saharon, Classification theory and the number of non-isomorphic models, North-Holland, Amstersdam, 1978.Google Scholar
[11] Shelah, Saharon, The spectrum problem. 1: ℵ ε -saturated models, the main gap, Israel Journal of Mathematics, vol. 43 (1982), pp. 324–356.CrossRefGoogle Scholar
[12] Shelah, Saharon, Classification theory for non-elementary classes. I: the number of uncountable models of . Parts A, B, Israel Journal of Mathematics, vol. 46 (1983), pp. 212–240, 241–273.CrossRefGoogle Scholar