Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-31T19:01:09.596Z Has data issue: false hasContentIssue false
  • English
  • Français

CLASSES OF BARREN EXTENSIONS

Part of: Extremal combinatorics Graph theory Model theory Set theory

Published online by Cambridge University Press:  05 October 2020

NATASHA DOBRINEN  and
DAN HATHAWAY
NATASHA DOBRINEN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF DENVER C.M. KNUDSON HALL ROOM 300-2390 S. YORK STREET DENVER, CO80208, USAE-mail: [email protected]: http://web.cs.du.edu/~ndobrine
DAN HATHAWAY
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF VERMONT INNOVATION HALL 82 UNIVERSITY PLACE BURLINGTON, VT05405, USAE-mail: [email protected]: https://www.uvm.edu/cems/mathstat/profiles/daniel-hathaway
Get access Rights & Permissions [Opens in a new window]

Abstract

Henle, Mathias, and Woodin proved in [21] that, provided that 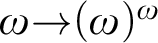${\omega }{\rightarrow }({\omega })^{{\omega }}$ holds in a model M of ZF, then forcing with 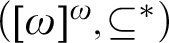$([{\omega }]^{{\omega }},{\subseteq }^*)$ over M adds no new sets of ordinals, thus earning the name a “barren” extension. Moreover, under an additional assumption, they proved that this generic extension preserves all strong partition cardinals. This forcing thus produces a model 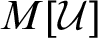$M[\mathcal {U}]$ , where 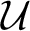$\mathcal {U}$ is a Ramsey ultrafilter, with many properties of the original model M. 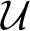This begged the question of how important the Ramseyness of $\mathcal {U}$ is for these results. In this paper, we show that several classes of 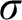$\sigma $ -closed forcings which generate non-Ramsey ultrafilters have the same properties. Such ultrafilters include Milliken–Taylor ultrafilters, a class of rapid p-points of Laflamme, k-arrow p-points of Baumgartner and Taylor, and extensions to a class of ultrafilters constructed by Dobrinen, Mijares, and Trujillo. Furthermore, the class of Boolean algebras 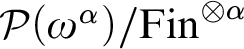$\mathcal {P}({\omega }^{{\alpha }})/{\mathrm {Fin}}^{\otimes {\alpha }}$ , 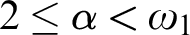$2\le {\alpha }<{\omega }_1$ , forcing non-p-points also produce barren extensions.

Keywords

ultrafiltersRamsey theoryforcingmodels without full choice

MSC classification

Primary: 03E02: Partition relations
Secondary: 03E05: Other combinatorial set theory 03C15: Denumerable structures 03E25: Axiom of choice and related propositions 05C55: Generalized Ramsey theory 05D10: Ramsey theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 1 , March 2021 , pp. 178 - 209
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Argyros, S. A. and Todorcevic, S., Ramsey Methods in Analysis , Birkhäuser, Basel, 2005.CrossRefGoogle Scholar
Baumgartner, J. E. and Taylor, A. D., Partition theorems and ultrafilters . Tansactions of the American Mathematical Society , vol. 241 (1978), pp. 283–309.CrossRefGoogle Scholar
Blass, A., The Rudin-Keisler ordering of P-points . Transactions of the American Mathematical Society , vol. 179 (1973), pp. 145–166.Google Scholar
Blass, A., Ultrafilters related to Hindman’s finite-unions theorem and its extensions . Contemporary Mathematics , vol. 65 (1987), pp. 89–124.CrossRefGoogle Scholar
Blass, A., Dobrinen, N., and Raghavan, D., The next best thing to a p-point , this Journal, vol. 80 (2015), no. 3, pp. 866–900.Google Scholar
Carlson, T. J. and Simpson, S. G., Topological Ramsey theory , Mathematics of Ramsey Theory (Nešetřil, J. and Rödl, V., editors), Algorithms and Combinatorics, vol. 5, Springer, New York, 1990, pp. 172–183.CrossRefGoogle Scholar
DiPrisco, C. A. and Todorcevic, S., Perfect-set properties in L(R)[U] . Advances in Mathematics , vol. 139 (1998), no. 2, pp. 240–259.CrossRefGoogle Scholar
DiPrisco, C., Mijares, J. G., and Nieto, J., Local Ramsey theory: An abstract approach . Mathematical Logic Quarterly , vol. 63 (2017), no. 5, pp. 384–396.Google Scholar
Dobrinen, N., Creature forcing and topological Ramsey spaces . Topology and Its Applications , vol. 213 (2016), pp. 110–126, Special issue in honor of Alan Dow’s 60th birthday.CrossRefGoogle Scholar
Dobrinen, N., High dimensional Ellentuck spaces and initial chains in the Tukey structure of non-p-points , this Journal, vol. 81 (2016), no. 1, pp. 237–263.Google Scholar
Dobrinen, N., Infinite dimensional Ellentuck spaces and Ramsey-classification theorems. Journal of Mathematical Logic , vol. 16 (2016), no. 1, p. 37.CrossRefGoogle Scholar
Dobrinen, N., Topological Ramsey spaces dense in forcings , Structure and Randomness in Computability and Set Theory (Cenzer, D., Porter, C., and J. Zapletal, editors), World Scientific, Singapore, 2020, p. 32.Google Scholar
Dobrinen, N. and Flores, S. N., Ramsey degrees of ultrafilters, pseudointersection numbers, and the tools of topological Ramsey spaces, submitted.Google Scholar
Dobrinen, N., Mijares, J. G., and Trujillo, T., Topological Ramsey spaces from Fraïssé classes, Ramsey-classification theorems, and initial structures in the Tukey types of p-points . Archive for Mathematical Logic , vol. 56 (2017), no. 7–8, pp. 733–782, Special Issue in Honor of James E. Baumgartner.CrossRefGoogle Scholar
Dobrinen, N. and Todorcevic, S., A new class of Ramsey-classification Theorems and their applications in the Tukey theory of ultrafilters, Part. Transactions of the American Mathematical Society , vol. 366 (2014), no. 3, pp. 1659–1684.10.1090/S0002-9947-2013-05844-8CrossRefGoogle Scholar
Dobrinen, N. and Todorcevic, S., A new class of Ramsey-classification theorems and their applications in the Tukey theory of ultrafilters, Part 2 . Transactions of the American Mathematical Society , vol. 367 (2015), no. 7, pp. 4627–4659.CrossRefGoogle Scholar
Ellentuck, E., A new proof that analytic sets are Ramsey , this Journal, vol. 39 (1974), no. 1, pp. 163–165.Google Scholar
Feng, Q., Magidor, M., and Woodin, H., Universally baire sets of reals , Set Theory of the Continuum (Woodin, H., Judah, H., and Just, W., editors), Mathematical Sciences Research Institute Publications, vol. 26, North-Holland, Amsterdam, 1992, pp. 203–242.CrossRefGoogle Scholar
Flores, S. N., Topological Ramsey space ideals , Ph.D. thesis, Universidad Nacional Autónoma de México, 2020.Google Scholar
Galvin, F. and Prikry, K., Borel sets and Ramsey’s theorem , this Journal, vol. 38 (1973), pp. 193–198.Google Scholar
Henle, J. M., Mathias, A. R. D., and Woodin, W. H., A barren extension , Methods in Mathematical Logic (Di Prisco, C. A., editor), Lecture Notes in Mathematics, vol. 1130, Springer, New York, 1985, pp. 195–207.CrossRefGoogle Scholar
Hrušák, M. and Verner, J. L., Adding ultrafilters by definable quotients . Rendiconti del Circolo Matematico di Palermo , vol. 60 (2011), no. 3, pp. 445–454.CrossRefGoogle Scholar
Jech, T., Set Theory , third millennium edition, revised and expanded, Springer, New York, NY, 2003.Google Scholar
Kurilić, M. S., Forcing with copies of countable ordinals . Proceedings of the American Mathematical Society , vol. 143 (2015), no. 4, pp. 1771–1784.CrossRefGoogle Scholar
Laflamme, C., Forcing with filters and complete combinatorics . Annals of Pure and Applied Logic , vol. 42 (1989), pp. 125–163.10.1016/0168-0072(89)90052-3CrossRefGoogle Scholar
Mathias, A. R. D., On a generalisation of Ramsey’s theorem , Ph.D. thesis, University of Cambridge, 1968.Google Scholar
Mathias, A. R. D., On sequences generic in the sense of Prikry . Journal of the Australian Mathematical Society , vol. 15 (1973), pp. 409–414.CrossRefGoogle Scholar
Mathias, A. R. D., Happy families . Annals of Mathematical Logic , vol. 12 (1977), no. 1, pp. 59–111.CrossRefGoogle Scholar
Mijares, J. G., A notion of selective ultrafilter corresponding to topological Ramsey spaces . Mathematical Logic Quarterly , vol. 53 (2007), no. 3, pp. 255–267.CrossRefGoogle Scholar
Mildenberger, H., On Milliken-Taylor ultrafilters . Notre Dame Journal of Formal Logic , vol. 52 (2011), no. 4, pp. 381–394.10.1215/00294527-1499345CrossRefGoogle Scholar
Nash-Williams, C. S. J. A., On well-quasi-ordering transfinite sequences . Proceedings of the Cambridge Philosophical Society , vol. 61 (1965), pp. 33–39.CrossRefGoogle Scholar
Nešetřil, J., Ramsey classes of set systems . Journal of Combinatorial Theory Series A , vol. 34 (1983), no. 2, pp. 183–201.CrossRefGoogle Scholar
Nešetřil, J. and Rödl, V., Partitions of finite relational and set systems . Journal of Combinatorial Theory Series A , vol. 22 (1977), no. 3, pp. 289–312.CrossRefGoogle Scholar
Prikry, K., Determinateness and partitions . Proceedings of the American Mathematical Society , vol. 54 (1976), no. 1, pp. 303–306.CrossRefGoogle Scholar
Shelah, S. and Woodin, H., Large cardinals imply that every reasonably definable set of reals is Lebesgue measurable . Israel Journal of Mathematics , vol. 70 (1990), pp. 381–384.CrossRefGoogle Scholar
Silver, J., Some applications of model theory in set theory . Annals of Mathematical Logic , vol. 3 (1971), no. 1, pp. 45–110.CrossRefGoogle Scholar
Steel, J. and Trang, N., AD+, derived models, and Σ1-reflection, 2010.Google Scholar
Szymański, A. and Xua, Z. H., The behaviour of ω2* under some consequences of Martin’s axiom , General Topology and Its Relations to Modern Analysis and Algebra , vol. V, Heldermann, Berlin, 1983, pp. 577–584.Google Scholar
Todorcevic, S., Introduction to Ramsey Spaces , Princeton University Press, Princeton, NJ, 2010.CrossRefGoogle Scholar
Trujillo, T., Topological Ramsey spaces, associated ultrafilters, and their applications to the Tukey theory of ultrafilters and Dedekind cuts of nonstandard arithmetic , Ph.D. thesis, University of Denver, 2014.Google Scholar
Woodin, W. H., Suitable extender models . Journal of Mathematical Logic , vol. 10 (2010), no. 01n02, pp. 101–339.CrossRefGoogle Scholar
Zheng, Y. Y., Selective ultrafilters on FIN . Proceedings of the American Mathematical Society , vol. 145 (2017), no. 12, pp. 5071–5086.CrossRefGoogle Scholar
Zheng, Y. Y., Preserved under Sacks forcing again? Acta Mathematica Hungarica , vol. 154 (2018), no. 1, pp. 1–28.CrossRefGoogle Scholar
Zheng, Y. Y., Parametrizing topological Ramsey spaces , Doctoral dissertation, 2018.Google Scholar