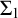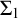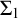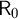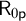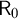1 Introduction
In this paper, we study certificates. These are theories-of-a-number with a free parameter for the number in question, or, more precisely, for the number-like object. In other words, certificates specify a property of a number. This property is roughly that the object specified is sufficiently like a number. A salient property of theories-of-a-number is that they have finite models.
The main focus of this paper is on certificates as a tool to metamathematical results. Thus, the paper can be viewed as a study of certificates as a method. We develop one specific certificate and provide the necessary lemmas for its employment. We apply the certificate to, possibly non-standard, witnesses of
![]() $\Sigma ^0_1$
-sentences. This use of the certificate is in constant interaction with the salient theories
$\Sigma ^0_1$
-sentences. This use of the certificate is in constant interaction with the salient theories
![]() $\mathsf {R}_0$
and
$\mathsf {R}_0$
and
![]() $\mathsf {R}$
. Our presentation provides more detail than previous presentations, so that many subtleties of what is going on become clearly visible here for the first time.
$\mathsf {R}$
. Our presentation provides more detail than previous presentations, so that many subtleties of what is going on become clearly visible here for the first time.
We extend the classical results obtained by the use of certificates by defining a wider class of theories, the
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theories. These theories behave in some important respects like the salient theory
$\mathsf {R}_{0\mathsf {p}}$
-sourced theories. These theories behave in some important respects like the salient theory
![]() $\mathsf {R}_0$
.
$\mathsf {R}_0$
.
The paper presents a number of applications of the use of certificates, which are important in themselves, but also serve to illustrate the use of the method well. These are:
-
• Certain theorems by Cobham and Vaught, the contents of which are explained in Section 2 below. We introduce these results in our preparatory Section 2. The detailed treatment then will be in Section 7. Our version of the second Vaught theorem is a generalization to the
 $\mathsf {R}_{0\mathsf {p}}$
-sourced case.
$\mathsf {R}_{0\mathsf {p}}$
-sourced case. -
• A variety of results concerning degree structures of interpretability. These results are in Section 8.
Theories-of-a-number have counterparts for various other data-types, like sets, multi-sets, sequences, and strings. The alternative that is developed and used is theories-of-a-finite-set. Here is a list of examples of uses of theories-of-a-number and their kin that we noted. We do not have any pretence of completeness here.
-
• In [Reference Friedman2], Harvey Friedman uses theories-of-a-number to prove the density of the interpretability degrees of finitely axiomatized theories. This result was proved earlier, by another method, in [Reference Mycielski, Pudlák and Stern10]. We present a version of the result in Theorem 8.9 and Corollary 8.11.
-
• In [Reference Visser20], Albert Visser uses theories-of-a-number to reprove (and improve) Vaught’s result [Reference Vaught18] that every c.e. Vaught theory is axiomatizable by a scheme.
-
• In [Reference Pakhomov11], Fedor Pakhomov uses theories-of-a-finite-set to construct an
 $\mathsf {R}$
-like set theory that proves its own consistency.
$\mathsf {R}$
-like set theory that proves its own consistency. -
• In [Reference Pakhomov and Visser12], Fedor Pakhomov and Albert Visser show the following. Consider a finitely axiomatised extension A of c.e. theory U in a possibly extended signature. Suppose A is conservative over U. Then, there is a conservative extension B of U in the signature of A, such that
 $A\vdash B$
and
$A\vdash B$
and
 $B \nvdash A$
. They use theories-of-a-finite-set to prove this result.
$B \nvdash A$
. They use theories-of-a-finite-set to prove this result.
1.1 Plan of the paper
The plan of the paper is as follows. In Section 2, we give a first presentation of both certain results by Cobham and Vaught and a preliminary explanation of the use of certificates. Section 3 fixes some basic definitions and provides pointers to relevant literature. In Section 4, we develop the basic facts about certificates of a
![]() $\Sigma ^0_1$
-witness and the theories
$\Sigma ^0_1$
-witness and the theories
![]() $\mathsf {R}_0$
and
$\mathsf {R}_0$
and
![]() $\mathsf {R}$
. In Section 5, we generalize the results of Section 4 by replacing
$\mathsf {R}$
. In Section 5, we generalize the results of Section 4 by replacing
![]() $\mathsf {R}_0$
by theories from a class that has
$\mathsf {R}_0$
by theories from a class that has
![]() $\mathsf {R}_0$
as its source. We provide examples to illustrate that many salient theories are in that class. Section 6 provides basic facts about witness comparison, which is an important tool that we use in the subsequent sections. The section is needed since the interaction between certificates and witness comparisons is somewhat delicate. In Section 7, we apply the methods developed in the previous sections to prove two theorems due to Vaught. Finally, in Section 8, we apply these methods to prove various results about degrees of interpretability. Sections 7 and 8 can be read independently of each other.
$\mathsf {R}_0$
as its source. We provide examples to illustrate that many salient theories are in that class. Section 6 provides basic facts about witness comparison, which is an important tool that we use in the subsequent sections. The section is needed since the interaction between certificates and witness comparisons is somewhat delicate. In Section 7, we apply the methods developed in the previous sections to prove two theorems due to Vaught. Finally, in Section 8, we apply these methods to prove various results about degrees of interpretability. Sections 7 and 8 can be read independently of each other.
1.2 History of the paper
The present paper succeeds and replaces Taishi Kurahashi’s earlier preprint Incompleteness and undecidability of theories consistent with
![]() $\mathsf {R}$
. The materials of the preprint are contained in the present paper.
$\mathsf {R}$
. The materials of the preprint are contained in the present paper.
2 Theorems of Cobham and Vaught
In this section, we give a presentation of current status of certain theorems of Cobham and Vaught. After some preparatory work, we take up this thread again in Section 7.
Let
![]() $\mathbb {L}_{\mathsf {a}}$
be the signature
$\mathbb {L}_{\mathsf {a}}$
be the signature
![]() $\{0, \mathsf {s}\hspace{0.02cm} , +, \times , \leqslant \}$
of first-order arithmetic. Let
$\{0, \mathsf {s}\hspace{0.02cm} , +, \times , \leqslant \}$
of first-order arithmetic. Let
![]() $\omega $
denote the set of all natural numbers. For each
$\omega $
denote the set of all natural numbers. For each
![]() $n \in \omega $
, the numeral
$n \in \omega $
, the numeral
![]() $\mathsf {s}\hspace{0.02cm} \ldots \mathsf {s}\hspace{0.02cm} 0$
(n applications of
$\mathsf {s}\hspace{0.02cm} \ldots \mathsf {s}\hspace{0.02cm} 0$
(n applications of
![]() $\mathsf {s}\hspace{0.02cm} $
) for n is denoted by
$\mathsf {s}\hspace{0.02cm} $
) for n is denoted by
![]() $\underline {n}$
. A central object of study in this paper is the
$\underline {n}$
. A central object of study in this paper is the
![]() $\mathbb {L}_{\mathsf {a}}$
-theory
$\mathbb {L}_{\mathsf {a}}$
-theory
![]() $\mathsf {R}$
introduced by Tarski, Mostowski, and Robinson in [Reference Tarski, Mostowski and Robinson15].
$\mathsf {R}$
introduced by Tarski, Mostowski, and Robinson in [Reference Tarski, Mostowski and Robinson15].
Definition 2.1 (The theory
 $\mathsf {R}$
)
$\mathsf {R}$
)
The theory
![]() $\mathsf {R}$
is axiomatized by the following sentences: For
$\mathsf {R}$
is axiomatized by the following sentences: For
![]() $m, n \in \omega $
,
$m, n \in \omega $
,
-
 $\mathsf {R}$
1.
$\mathsf {R}$
1.
 $\underline {m} + \underline {n} = \underline {m + n}$
$\underline {m} + \underline {n} = \underline {m + n}$
-
 $\mathsf {R}$
2.
$\mathsf {R}$
2.
 $\underline {m} \times \underline {n} = \underline {m \times n}$
$\underline {m} \times \underline {n} = \underline {m \times n}$
-
 $\mathsf {R}$
3.
$\mathsf {R}$
3.
 $\underline {m} \neq \underline {n}$
(if
$\underline {m} \neq \underline {n}$
(if
 $m \neq n$
)
$m \neq n$
) -
 $\mathsf {R}$
4.
$\mathsf {R}$
4.
 $\forall x\, \bigl (x \mathbin {\leqslant } \underline {n} \to \bigvee _{i \mathbin {\leqslant } n} x = \underline {i}\bigr )$
$\forall x\, \bigl (x \mathbin {\leqslant } \underline {n} \to \bigvee _{i \mathbin {\leqslant } n} x = \underline {i}\bigr )$
-
 $\mathsf {R}$
5.
$\mathsf {R}$
5.
 $\forall x\, (x \leqslant \underline {n} \lor \underline {n} \leqslant x).$
$\forall x\, (x \leqslant \underline {n} \lor \underline {n} \leqslant x).$
It was proved in [Reference Tarski, Mostowski and Robinson15] that the original
![]() $\mathsf {R}$
is essentially undecidable, that is, every consistent extension of
$\mathsf {R}$
is essentially undecidable, that is, every consistent extension of
![]() $\mathsf {R}$
is undecidable. Here, we comment on the difference between our formulation and the original one of the theory
$\mathsf {R}$
is undecidable. Here, we comment on the difference between our formulation and the original one of the theory
![]() $\mathsf {R}$
. The signature adopted in [Reference Tarski, Mostowski and Robinson15] does not contain the symbol
$\mathsf {R}$
. The signature adopted in [Reference Tarski, Mostowski and Robinson15] does not contain the symbol
![]() $\leqslant $
and the formula
$\leqslant $
and the formula
![]() $x \leqslant y$
is introduced as the abbreviation for
$x \leqslant y$
is introduced as the abbreviation for
![]() $\exists z \; z + x = y$
. Our signature
$\exists z \; z + x = y$
. Our signature
![]() $\mathbb {L}_{\mathsf {a}}$
contains
$\mathbb {L}_{\mathsf {a}}$
contains
![]() $\leqslant $
as a primitive symbol and our version of
$\leqslant $
as a primitive symbol and our version of
![]() $\mathsf {R}$
does not prove the equivalence between the formulas
$\mathsf {R}$
does not prove the equivalence between the formulas
![]() $x \leqslant y$
and
$x \leqslant y$
and
![]() $\exists z \; z + x = y$
. So, our
$\exists z \; z + x = y$
. So, our
![]() $\mathsf {R}$
is strictly weaker than the original. Jones and Shepherdson [Reference Jones and Shepherdson6] pointed out that the essential undecidability of
$\mathsf {R}$
is strictly weaker than the original. Jones and Shepherdson [Reference Jones and Shepherdson6] pointed out that the essential undecidability of
![]() $\mathsf {R}$
also holds without using the equivalence
$\mathsf {R}$
also holds without using the equivalence
![]() $x \leqslant y \leftrightarrow \exists z \; z + x = y$
.
$x \leqslant y \leftrightarrow \exists z \; z + x = y$
.
The
![]() $\mathbb {L}_{\mathsf {a}}$
-theory
$\mathbb {L}_{\mathsf {a}}$
-theory
![]() $\mathsf {R}_0$
is obtained from
$\mathsf {R}_0$
is obtained from
![]() $\mathsf {R}$
by replacing the axiom
$\mathsf {R}$
by replacing the axiom
![]() $\mathsf {R5}$
with the following
$\mathsf {R5}$
with the following
![]() $\mathsf {R5'}$
:
$\mathsf {R5'}$
:
-
 $\mathsf {R5'}$
:
$\mathsf {R5'}$
:
 $\underline {m} \leqslant \underline {n}$
(if
$\underline {m} \leqslant \underline {n}$
(if
 $m \leqslant n$
) .
$m \leqslant n$
) .
Alternatively, we can axiomatize
![]() $\mathsf {R}_0$
by dropping
$\mathsf {R}_0$
by dropping
![]() $\mathsf {R5}$
altogether and replacing
$\mathsf {R5}$
altogether and replacing
![]() $\mathsf {R4}$
by:
$\mathsf {R4}$
by:
-
 $\mathsf {R4'}$
:
$\mathsf {R4'}$
:
 $\forall x\, \bigl (x \mathbin {\leqslant } \underline {n} \leftrightarrow \bigvee _{i \mathbin {\leqslant } n} x = \underline {i}\bigr ).$
$\forall x\, \bigl (x \mathbin {\leqslant } \underline {n} \leftrightarrow \bigvee _{i \mathbin {\leqslant } n} x = \underline {i}\bigr ).$
We make
![]() $\mathsf {R1}$
-
$\mathsf {R1}$
-
![]() $\mathsf {4}$
plus
$\mathsf {4}$
plus
![]() $\mathsf {R5'}$
our official axiomatization.
$\mathsf {R5'}$
our official axiomatization.
Remark 2.2. Our definitions of
![]() $\mathsf {R}$
and
$\mathsf {R}$
and
![]() $\mathsf {R}_0$
correspond to those in Švejdar’s paper [Reference Švejdar and Peliš14]. Vaught’s definition of
$\mathsf {R}_0$
correspond to those in Švejdar’s paper [Reference Švejdar and Peliš14]. Vaught’s definition of
![]() $\mathsf {R}_0$
in [Reference Vaught17] is in the same spirit as ours, but still differs. He presents the theory in a relational format without identity. There is a mistake in Vaught’s statement of the axioms. The theory as given in the paper clearly has a decidable extension. As possible repairs, one could add the axioms for the totality of the functions or replace, both in Axiom I and II, the second occurrence of
$\mathsf {R}_0$
in [Reference Vaught17] is in the same spirit as ours, but still differs. He presents the theory in a relational format without identity. There is a mistake in Vaught’s statement of the axioms. The theory as given in the paper clearly has a decidable extension. As possible repairs, one could add the axioms for the totality of the functions or replace, both in Axiom I and II, the second occurrence of
![]() $\to $
by
$\to $
by
![]() $\leftrightarrow $
. Jones and Shepherdson in [Reference Jones and Shepherdson6] discuss both the version of
$\leftrightarrow $
. Jones and Shepherdson in [Reference Jones and Shepherdson6] discuss both the version of
![]() $\mathsf {R}$
with and without a defined relation
$\mathsf {R}$
with and without a defined relation
![]() $\leqslant $
. They use
$\leqslant $
. They use
![]() $\mathsf {R}^{\prime }_0$
for our
$\mathsf {R}^{\prime }_0$
for our
![]() $\mathsf {R}_0$
.
$\mathsf {R}_0$
.
It is easy to see that
![]() $\mathsf {R}_0$
is a proper subtheory of
$\mathsf {R}_0$
is a proper subtheory of
![]() $\mathsf {R}$
. We note that all the axioms of
$\mathsf {R}$
. We note that all the axioms of
![]() $\mathsf {R}_0$
can be rewritten as
$\mathsf {R}_0$
can be rewritten as
![]() $\Delta _0$
-formulas. This leads to a nice observation by Vítězslav Švejdar.
$\Delta _0$
-formulas. This leads to a nice observation by Vítězslav Švejdar.
Theorem 2.3 (Cf. Švejdar [Reference Švejdar and Peliš14])
An
![]() $\mathbb {L}_{\mathsf {a}}$
-theory T is
$\mathbb {L}_{\mathsf {a}}$
-theory T is
![]() $\Sigma _1$
-complete if and only if
$\Sigma _1$
-complete if and only if
![]() $T \vdash \mathsf {R}_0$
.
$T \vdash \mathsf {R}_0$
.
Cobham observed that
![]() $\mathsf {R}$
is interpretable in
$\mathsf {R}$
is interpretable in
![]() $\mathsf {R}_0$
, and that, hence,
$\mathsf {R}_0$
, and that, hence,
![]() $\mathsf {R}_0$
is essentially undecidable (see Vaught [Reference Vaught17] and Jones and Shepherdson [Reference Jones and Shepherdson6]).Footnote
1
We give Cobham’s interpretation in Section 7.
$\mathsf {R}_0$
is essentially undecidable (see Vaught [Reference Vaught17] and Jones and Shepherdson [Reference Jones and Shepherdson6]).Footnote
1
We give Cobham’s interpretation in Section 7.
In the formulation of
![]() $\mathsf {R}_0$
, if
$\mathsf {R}_0$
, if
![]() $x \leqslant y$
is defined by
$x \leqslant y$
is defined by
![]() $\exists z \; z + x = y$
as in [Reference Tarski, Mostowski and Robinson15], rather than primitive as in the present paper, then the axiom
$\exists z \; z + x = y$
as in [Reference Tarski, Mostowski and Robinson15], rather than primitive as in the present paper, then the axiom
![]() $\mathsf {R5'}$
is redundant since it can be derived from
$\mathsf {R5'}$
is redundant since it can be derived from
![]() $\textsf {R1}$
. On the other hand, note that, in our signature
$\textsf {R1}$
. On the other hand, note that, in our signature
![]() $\mathbb {L}_{\mathsf {a}}$
, the theory obtained from
$\mathbb {L}_{\mathsf {a}}$
, the theory obtained from
![]() $\mathsf {R}_0$
by removing
$\mathsf {R}_0$
by removing
![]() $\mathsf {R5'}$
has a complete consistent decidable extension (see Jones and Shepherdson [Reference Jones and Shepherdson6]).
$\mathsf {R5'}$
has a complete consistent decidable extension (see Jones and Shepherdson [Reference Jones and Shepherdson6]).
We say that a theory T is essentially hereditarily undecidable if every
![]() $\mathbb {L}_{\mathsf {a}}$
-theory consistent with T is undecidable (cf. [Reference Visser26]). It is shown in [Reference Tarski, Mostowski and Robinson15] that every finitely axiomatized essentially undecidable theory is also essentially hereditarily undecidable. Here, since the theory
$\mathbb {L}_{\mathsf {a}}$
-theory consistent with T is undecidable (cf. [Reference Visser26]). It is shown in [Reference Tarski, Mostowski and Robinson15] that every finitely axiomatized essentially undecidable theory is also essentially hereditarily undecidable. Here, since the theory
![]() $\mathsf {R}_0$
is not finitely axiomatizable, it is nontrivial whether
$\mathsf {R}_0$
is not finitely axiomatizable, it is nontrivial whether
![]() $\mathsf {R}_0$
is essentially hereditarily undecidable. In fact, there exists a computably axiomatized essentially undecidable theory having a decidable subtheory (cf. Ehrenfeucht [Reference Ehrenfeucht1] and Putnam [Reference Putnam13]). Then, Cobham proved the following interesting theorem.
$\mathsf {R}_0$
is essentially hereditarily undecidable. In fact, there exists a computably axiomatized essentially undecidable theory having a decidable subtheory (cf. Ehrenfeucht [Reference Ehrenfeucht1] and Putnam [Reference Putnam13]). Then, Cobham proved the following interesting theorem.
Theorem 2.4 (Cobham, see Vaught [Reference Vaught17, Theorem 1.5])
The theory
![]() $\mathsf {R}_0$
is essentially hereditarily undecidable.
$\mathsf {R}_0$
is essentially hereditarily undecidable.
A proof of Cobham’s theorem was presented in Vaught [Reference Vaught17]. Vaught also showed two strengthenings of Cobham’s theorem.
For each
![]() $i \in \omega $
, let
$i \in \omega $
, let
![]() $\mathsf {W}_{i}$
denote the c.e. set with the index i. We say that a pair
$\mathsf {W}_{i}$
denote the c.e. set with the index i. We say that a pair
![]() $(X, Y)$
of disjoint c.e. sets is effectively inseparable if for any
$(X, Y)$
of disjoint c.e. sets is effectively inseparable if for any
![]() $i, j \in \omega $
, if
$i, j \in \omega $
, if
![]() $X \subseteq \mathsf {W}_{i}$
,
$X \subseteq \mathsf {W}_{i}$
,
![]() $Y \subseteq \mathsf {W}_{j}$
, and
$Y \subseteq \mathsf {W}_{j}$
, and
![]() $\mathsf {W}_{i} \cap \mathsf {W}_{j} = \emptyset $
, then we can effectively find an element x such that
$\mathsf {W}_{i} \cap \mathsf {W}_{j} = \emptyset $
, then we can effectively find an element x such that
![]() $x \notin \mathsf {W}_{i} \cup \mathsf {W}_{j}$
. For each theory T, let
$x \notin \mathsf {W}_{i} \cup \mathsf {W}_{j}$
. For each theory T, let
![]() $T_{\mathfrak {p}}$
and
$T_{\mathfrak {p}}$
and
![]() $T_{\mathfrak {r}}$
be the set of all theorems of T and the set of all sentences refutable in T, respectively. We say that a consistent theory T is strongly effectively inseparable if the pair
$T_{\mathfrak {r}}$
be the set of all theorems of T and the set of all sentences refutable in T, respectively. We say that a consistent theory T is strongly effectively inseparable if the pair
![]() $(T_{\mathfrak {p}}, \emptyset _{\mathfrak {r}})$
is effectively inseparable (cf. [Reference Kurahashi and Visser9]). The first strengthening is the following.
$(T_{\mathfrak {p}}, \emptyset _{\mathfrak {r}})$
is effectively inseparable (cf. [Reference Kurahashi and Visser9]). The first strengthening is the following.
Theorem 2.5 (Vaught [Reference Vaught17, Theorem 5.2])
The theory
![]() $\mathsf {R}_0$
is strongly effectively inseparable.
$\mathsf {R}_0$
is strongly effectively inseparable.
In fact, Cobham’s theorem follows easily from Theorem 2.5. The second one is the following theorem that immediately implies Cobham’s theorem, but no proof was presented in Vaught’s paper.
Theorem 2.6 (Vaught [Reference Vaught17, Theorem 7.1])
For any c.e.
![]() $\mathbb {L}_{\mathsf {a}}$
-theory U, if
$\mathbb {L}_{\mathsf {a}}$
-theory U, if
![]() $\mathsf {R}_0 + U$
is consistent, then there exists a finitely axiomatized
$\mathsf {R}_0 + U$
is consistent, then there exists a finitely axiomatized
![]() $\mathbb {L}_{\mathsf {a}}$
-theory S extending
$\mathbb {L}_{\mathsf {a}}$
-theory S extending
![]() $\mathsf {R}_0$
such that
$\mathsf {R}_0$
such that
![]() $S + U$
is also consistent.
$S + U$
is also consistent.
Recently, a more comprehensible proof of Cobham’s theorem (Theorem 2.4) was also given in Visser [Reference Visser22].
Definition 2.7 (Pure
 $\Delta _0$
- and
$\Delta _0$
- and
 $\Sigma _1$
-formulas)
$\Sigma _1$
-formulas)
Let
![]() $\varphi $
be an
$\varphi $
be an
![]() $\mathbb {L}_{\mathsf {a}}$
-formula.
$\mathbb {L}_{\mathsf {a}}$
-formula.
-
• We say that
 $\varphi $
is a pure
$\varphi $
is a pure
 $\Delta _0$
-formula if
$\Delta _0$
-formula if
 $\varphi $
is
$\varphi $
is
 $\Delta _0$
and satisfies the following conditions:
$\Delta _0$
and satisfies the following conditions:-
1. For any atomic formula of the form
 $t_1 \leqslant t_2$
contained in
$t_1 \leqslant t_2$
contained in
 $\varphi $
, terms
$\varphi $
, terms
 $t_1$
and
$t_1$
and
 $t_2$
are both variables;
$t_2$
are both variables; -
2. Every atomic formula of the form
 $t_1 = t_2$
contained in
$t_1 = t_2$
contained in
 $\varphi $
is of one of the forms
$\varphi $
is of one of the forms
 $x_0 = x_1$
,
$x_0 = x_1$
,
 $0 = x_0$
,
$0 = x_0$
,
 $\mathsf {s}\hspace{0.02cm} x_0 = x_1$
,
$\mathsf {s}\hspace{0.02cm} x_0 = x_1$
,
 $x_0 + x_1 = x_2$
, and
$x_0 + x_1 = x_2$
, and
 $x_0 \times x_1 = x_2$
, where
$x_0 \times x_1 = x_2$
, where
 $x_0$
,
$x_0$
,
 $x_1$
, and
$x_1$
, and
 $x_2$
are variables.
$x_2$
are variables.
-
-
• We say that
 $\varphi $
is a pure
$\varphi $
is a pure
 $\Sigma _1$
-formula if
$\Sigma _1$
-formula if
 $\varphi $
is of the form
$\varphi $
is of the form
 $\exists \vec {x}\, \varphi _0(\vec {x})$
, where
$\exists \vec {x}\, \varphi _0(\vec {x})$
, where
 $\varphi _0(\vec {x})$
is a pure
$\varphi _0(\vec {x})$
is a pure
 $\Delta _0$
-formula. Here, the block
$\Delta _0$
-formula. Here, the block
 $\vec {x}$
of quantifiers is allowed to be empty.
$\vec {x}$
of quantifiers is allowed to be empty.
Our version of predicate logic does not contain the logical constants
![]() $\top $
and
$\top $
and
![]() $\bot $
as primitive symbols. It is then shown that every pure
$\bot $
as primitive symbols. It is then shown that every pure
![]() $\Delta _0$
-formula contains at least one free variable. An effective procedure to obtain an equivalent pure
$\Delta _0$
-formula contains at least one free variable. An effective procedure to obtain an equivalent pure
![]() $\Sigma _1$
-formula for each
$\Sigma _1$
-formula for each
![]() $\Sigma _1$
-formula is presented in [Reference Visser22].
$\Sigma _1$
-formula is presented in [Reference Visser22].
Proposition 2.8 (Visser [Reference Visser22])
For any
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (\vec {x})$
, a pure
$\varphi (\vec {x})$
, a pure
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi ^\circ (\vec {x})$
satisfying the following conditions is effectively found:
$\varphi ^\circ (\vec {x})$
satisfying the following conditions is effectively found:
-
1.
 $\mathbb {N} \models \forall \vec {x} \, (\varphi (\vec {x}) \leftrightarrow \varphi ^\circ (\vec {x}))$
,
$\mathbb {N} \models \forall \vec {x} \, (\varphi (\vec {x}) \leftrightarrow \varphi ^\circ (\vec {x}))$
, -
2.
 $\forall \vec {x} \, (\varphi ^\circ (\vec {x}) \to \varphi (\vec {x}))$
is logically valid.
$\forall \vec {x} \, (\varphi ^\circ (\vec {x}) \to \varphi (\vec {x}))$
is logically valid.
Here, we outline the proof of Cobham’s theorem presented in [Reference Visser22]. At first, the finite
![]() $\mathbb {L}_{\mathsf {a}}$
-theory
$\mathbb {L}_{\mathsf {a}}$
-theory
![]() $\mathsf {TN}$
(the theory of a number) is introduced. Then, for each pure
$\mathsf {TN}$
(the theory of a number) is introduced. Then, for each pure
![]() $\Sigma _1$
-sentence of the form
$\Sigma _1$
-sentence of the form
![]() $\exists \vec {x}\, \sigma _0(\vec {x})$
, where
$\exists \vec {x}\, \sigma _0(\vec {x})$
, where
![]() $\sigma _0(\vec {x})$
is a pure
$\sigma _0(\vec {x})$
is a pure
![]() $\Delta _0$
-formula, let
$\Delta _0$
-formula, let
![]() ${[ \sigma ]}$
be the finite
${[ \sigma ]}$
be the finite
![]() $\mathbb {L}_{\mathsf {a}}$
-theory
$\mathbb {L}_{\mathsf {a}}$
-theory
Let
![]() $\sigma ^\star $
be an
$\sigma ^\star $
be an
![]() $\mathbb {L}_{\mathsf {a}}$
-sentence saying that there exists the least number n such that the finite
$\mathbb {L}_{\mathsf {a}}$
-sentence saying that there exists the least number n such that the finite
![]() $\mathbb {L}_{\mathsf {a}}$
-structure
$\mathbb {L}_{\mathsf {a}}$
-structure
![]() $\{0, 1, \ldots , n\}$
is a model of
$\{0, 1, \ldots , n\}$
is a model of
![]() ${[ \sigma ]}$
. Then, the following three clauses hold for each pure
${[ \sigma ]}$
. Then, the following three clauses hold for each pure
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\sigma $
:
$\sigma $
:
-
1. If
 $\mathbb {N} \models \sigma $
, then
$\mathbb {N} \models \sigma $
, then
 $\mathsf {R}_0 \vdash \sigma ^\star $
.
$\mathsf {R}_0 \vdash \sigma ^\star $
. -
2. If
 $\mathbb {N} \models \neg \, \sigma $
, then
$\mathbb {N} \models \neg \, \sigma $
, then
 ${[ \sigma ]} \vdash \mathsf {R}_0$
.
${[ \sigma ]} \vdash \mathsf {R}_0$
. -
3.
 $(\mathsf {R}_0 + \sigma ^\star ) \vartriangleright {[ \sigma ]}$
.
$(\mathsf {R}_0 + \sigma ^\star ) \vartriangleright {[ \sigma ]}$
.
Here,
![]() $T \vartriangleright T'$
means that
$T \vartriangleright T'$
means that
![]() $T'$
is interpretable in T (see Section 3 for the definition). Let U be any
$T'$
is interpretable in T (see Section 3 for the definition). Let U be any
![]() $\mathbb {L}_{\mathsf {a}}$
-theory such that
$\mathbb {L}_{\mathsf {a}}$
-theory such that
![]() $\mathsf {R}_0 + U$
is consistent. We would like to show that U is undecidable. We may assume that U is a c.e. theory. Then, the set
$\mathsf {R}_0 + U$
is consistent. We would like to show that U is undecidable. We may assume that U is a c.e. theory. Then, the set
![]() $X : = \{\sigma \mid \sigma $
is a pure
$X : = \{\sigma \mid \sigma $
is a pure
![]() $\Sigma _1$
sentence and
$\Sigma _1$
sentence and
![]() $\mathsf {R}_0 + \sigma ^\star + U$
is consistent
$\mathsf {R}_0 + \sigma ^\star + U$
is consistent
![]() $\}$
is
$\}$
is
![]() $\Pi _1$
-definable. Since the set
$\Pi _1$
-definable. Since the set
![]() $Y : = \{\sigma \mid \sigma $
is a true pure
$Y : = \{\sigma \mid \sigma $
is a true pure
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\}$
is not
$\}$
is not
![]() $\Pi _1$
-definable, we have
$\Pi _1$
-definable, we have
![]() $X \neq Y$
. By the first clause above, we have
$X \neq Y$
. By the first clause above, we have
![]() $Y \subsetneq X$
, and hence
$Y \subsetneq X$
, and hence
![]() $X \nsubseteq Y$
. Then, we get a false pure
$X \nsubseteq Y$
. Then, we get a false pure
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\sigma $
such that
$\sigma $
such that
![]() $\mathsf {R}_0 + \sigma ^\star + U$
is consistent. By the second clause, we have
$\mathsf {R}_0 + \sigma ^\star + U$
is consistent. By the second clause, we have
![]() ${[ \sigma ]} \vdash \mathsf {R}_0$
, and thus the theory
${[ \sigma ]} \vdash \mathsf {R}_0$
, and thus the theory
![]() ${[ \sigma ]}$
is essentially undecidable. Since
${[ \sigma ]}$
is essentially undecidable. Since
![]() ${[ \sigma ]}$
is finite and
${[ \sigma ]}$
is finite and
![]() $(\mathsf {R}_0 + \sigma ^\star ) \vartriangleright {[ \sigma ]}$
by the third clause, there exists a finite subtheory S of
$(\mathsf {R}_0 + \sigma ^\star ) \vartriangleright {[ \sigma ]}$
by the third clause, there exists a finite subtheory S of
![]() $\mathsf {R}_0 + \sigma ^\star $
such that
$\mathsf {R}_0 + \sigma ^\star $
such that
![]() $S \vartriangleright {[ \sigma ]}$
. Then, S is essentially undecidable and
$S \vartriangleright {[ \sigma ]}$
. Then, S is essentially undecidable and
![]() $S + U$
is consistent. Since S is finite, we conclude that U is undecidable.
$S + U$
is consistent. Since S is finite, we conclude that U is undecidable.
However, it seems that the proof by Visser cannot be used to prove Vaught’s theorems (Theorems 2.5 and 2.6) as it is, because the notion of interpretability between theories is used in it.
In this paper, we prove the following theorem using a modification of Visser’s strategy.
Theorem 2.9 (Certified extension theorem)
For each
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\sigma $
, we can effectively find a sentence
$\sigma $
, we can effectively find a sentence
![]() ${[ \sigma ]}$
satisfying the following conditions:
${[ \sigma ]}$
satisfying the following conditions:
-
1.
 $ {[ \sigma ]} \vdash \sigma $
.
$ {[ \sigma ]} \vdash \sigma $
. -
2. If
 $\mathbb {N} \models \sigma $
, then
$\mathbb {N} \models \sigma $
, then
 $\mathsf {R}_0 \vdash {[ \sigma ]}$
.
$\mathsf {R}_0 \vdash {[ \sigma ]}$
. -
3. If
 $\mathbb {N} \models \neg \, \sigma $
, then
$\mathbb {N} \models \neg \, \sigma $
, then
 ${[ \sigma ]} \vdash \mathsf {R}_0$
.
${[ \sigma ]} \vdash \mathsf {R}_0$
.
We call such sentences
![]() ${[ \sigma ]}$
certified
${[ \sigma ]}$
certified
![]() $\Sigma _1$
-sentences for
$\Sigma _1$
-sentences for
![]() $\mathsf {R}_0$
.
$\mathsf {R}_0$
.
We note that Visser’s
![]() $[\sigma ]$
does give us the analogs of (1) and (3) of Theorem 2.9. However the analog of (2) fails. We only get: if
$[\sigma ]$
does give us the analogs of (1) and (3) of Theorem 2.9. However the analog of (2) fails. We only get: if
![]() $\mathbb {N} \models \sigma $
, then
$\mathbb {N} \models \sigma $
, then
![]() $\mathsf {R}_0 \rhd [\sigma ]$
.
$\mathsf {R}_0 \rhd [\sigma ]$
.
3 Basic definitions
We only present a brief outline of the basic notions. For more detail, we refer the reader to, e.g., [Reference Visser22, Appendix A].
A theory U in this paper is a theory of predicate logic of finite signature
![]() $\varTheta $
. A theory U is given by a finite signature
$\varTheta $
. A theory U is given by a finite signature
![]() $\varTheta $
and a set of axioms X of the signature
$\varTheta $
and a set of axioms X of the signature
![]() $\varTheta $
.
$\varTheta $
.
Definition 3.1. The conjunction of the finitely many axioms for identity of U is
![]() $\mathfrak {id}_{\varTheta }$
or
$\mathfrak {id}_{\varTheta }$
or
![]() $\mathfrak {id}_{U}$
. The axioms of identity are officially part of the logic but at times we will treat them as if they were part of the axioms of the theory.
$\mathfrak {id}_{U}$
. The axioms of identity are officially part of the logic but at times we will treat them as if they were part of the axioms of the theory.
Let us fix an infinite sequence of variables
![]() $v_0,v_1,\dots $
. Suppose
$v_0,v_1,\dots $
. Suppose
![]() $\varTheta $
is a relational signature. A one-dimensional parameter-free translation
$\varTheta $
is a relational signature. A one-dimensional parameter-free translation
![]() $\tau :\varTheta \to \varXi $
specifies a domain predicate
$\tau :\varTheta \to \varXi $
specifies a domain predicate
![]() $\delta _\tau $
, with at most
$\delta _\tau $
, with at most
![]() $v_0$
free, and, for an n-ary predicate symbol R of
$v_0$
free, and, for an n-ary predicate symbol R of
![]() $\varTheta $
a
$\varTheta $
a
![]() $\varXi $
-formula
$\varXi $
-formula
![]() $R_\tau $
, such that the free variables of
$R_\tau $
, such that the free variables of
![]() $R_\tau $
are among
$R_\tau $
are among
![]() $v_0,\dots ,v_{n-1}$
. We treat identity as if it were a predicate from the signature rather than a logical predicate. We lift the translation to the full
$v_0,\dots ,v_{n-1}$
. We treat identity as if it were a predicate from the signature rather than a logical predicate. We lift the translation to the full
![]() $\varTheta $
-signature as follows:
$\varTheta $
-signature as follows:
-
•
 $(R(\vec {x}))^\tau := R_\tau [\vec {v}:= \vec {x}]$
. Here we assume an automatic mechanism of renaming variables in case of clashes.
$(R(\vec {x}))^\tau := R_\tau [\vec {v}:= \vec {x}]$
. Here we assume an automatic mechanism of renaming variables in case of clashes. -
•
 $(\cdot )^\tau $
commutes with the propositional connectives.
$(\cdot )^\tau $
commutes with the propositional connectives. -
•
 $(\forall x \psi )^\tau := \forall x\, (\delta _\tau [v_0:= x] \to \psi ^\tau )$
.
$(\forall x \psi )^\tau := \forall x\, (\delta _\tau [v_0:= x] \to \psi ^\tau )$
. -
•
 $(\exists x \psi )^\tau := \exists x\, (\delta _\tau [v_0:= x] \wedge \psi ^\tau )$
.
$(\exists x \psi )^\tau := \exists x\, (\delta _\tau [v_0:= x] \wedge \psi ^\tau )$
.
If
![]() $\varGamma $
is a set of
$\varGamma $
is a set of
![]() $\varTheta $
-sentences, we write
$\varTheta $
-sentences, we write
![]() $\varGamma ^\tau $
for
$\varGamma ^\tau $
for
![]() $\{ \phi ^\tau \mid \phi \in \varGamma \}$
.
$\{ \phi ^\tau \mid \phi \in \varGamma \}$
.
We can extend translations to m-dimensional ones by translating a variable from the
![]() $\varTheta $
-signature to a sequence of variables of length m of the
$\varTheta $
-signature to a sequence of variables of length m of the
![]() $\varXi $
-signature. We can also allow parameters in our interpretations.
$\varXi $
-signature. We can also allow parameters in our interpretations.
We can define the identity translation and composition of translations in the obvious way.
An interpretation
![]() $\mathsf {K}$
of U in V is a triple
$\mathsf {K}$
of U in V is a triple
![]() $(U,\tau , V)$
, where
$(U,\tau , V)$
, where
![]() $\tau $
is a translation from the signature
$\tau $
is a translation from the signature
![]() $\Theta _U$
of U to the signature
$\Theta _U$
of U to the signature
![]() $\Theta _V$
of V. We demand that, for every U-sentence
$\Theta _V$
of V. We demand that, for every U-sentence
![]() $\phi $
such that
$\phi $
such that
![]() $U \vdash \phi $
, we have
$U \vdash \phi $
, we have
![]() $V\vdash \phi ^\tau $
. We write
$V\vdash \phi ^\tau $
. We write
![]() $\mathsf {K}:U \lhd V$
or
$\mathsf {K}:U \lhd V$
or
![]() $\mathsf {K}: V \rhd U$
for
$\mathsf {K}: V \rhd U$
for
![]() $\mathsf {K}$
is an interpretation of U in V. We write
$\mathsf {K}$
is an interpretation of U in V. We write
![]() $U\lhd V$
or
$U\lhd V$
or
![]() $V\rhd U$
for: there is a
$V\rhd U$
for: there is a
![]() $\mathsf {K}$
such that
$\mathsf {K}$
such that
![]() $\mathsf {K}:U \lhd V$
.
$\mathsf {K}:U \lhd V$
.
We have also the notion of local interpretability. The theory V locally interprets the theory U, or
![]() $V \rhd _{\mathsf {loc}}U$
, iff for each finitely axiomatized subtheory
$V \rhd _{\mathsf {loc}}U$
, iff for each finitely axiomatized subtheory
![]() $U_0$
of U, we have
$U_0$
of U, we have
![]() $V \rhd U_0$
.
$V \rhd U_0$
.
We will make use of the following operations on theories. Consider theories U and V.
-
• The theory
 is defined as follows. The signature of
is defined as follows. The signature of  is the disjoint sum of the signatures of U and V and, in addition, a fresh 0-ary predicate P. The axioms of
is the disjoint sum of the signatures of U and V and, in addition, a fresh 0-ary predicate P. The axioms of  are all
are all
 $P \to \phi $
, where
$P \to \phi $
, where
 $\phi $
is an axiom of U, plus all
$\phi $
is an axiom of U, plus all
 $\neg \, P \to \psi $
, where
$\neg \, P \to \psi $
, where
 $\psi $
is an axiom of V.
$\psi $
is an axiom of V. -
• The theory
 is defined as follows. The signature of
is defined as follows. The signature of  is the disjoint sum of the signatures of U and V and, in addition, a fresh 1-ary predicate
is the disjoint sum of the signatures of U and V and, in addition, a fresh 1-ary predicate
 $\triangle $
. The axioms of
$\triangle $
. The axioms of  are the relativizations
are the relativizations
 $\phi ^\triangle $
of all axioms of
$\phi ^\triangle $
of all axioms of
 $\phi $
of U w.r.t.
$\phi $
of U w.r.t.
 $\triangle $
, plus the relativizations
$\triangle $
, plus the relativizations
 $\psi ^{\neg \,\triangle }$
of all axioms of
$\psi ^{\neg \,\triangle }$
of all axioms of
 $\psi $
of V with respect to the complement of
$\psi $
of V with respect to the complement of
 $\triangle $
, plus axioms saying that neither
$\triangle $
, plus axioms saying that neither
 $\triangle $
nor its complement are empty.
$\triangle $
nor its complement are empty.
We have the following important properties.
Theorem 3.2.
-
a.
 iff
iff
 $U\rhd W$
and
$U\rhd W$
and
 $V \rhd W$
.
$V \rhd W$
. -
b.
 iff
iff
 $W\rhd U$
and
$W\rhd U$
and
 $W \rhd V$
.
$W \rhd V$
.
Thus, ![]() is (an implementation of) the infimum of U and V in the degrees of interpretability and
is (an implementation of) the infimum of U and V in the degrees of interpretability and ![]() is (an implementation of) the supremum of U and V in the degrees of interpretability. There is something notationally awkward about representing an infimum by
is (an implementation of) the supremum of U and V in the degrees of interpretability. There is something notationally awkward about representing an infimum by ![]() and a supremum by
and a supremum by ![]() . This awkwardness is due to a legacy problem. In the boolean intuition the most informative element is the bottom, where in the interpretation-ordering the most informative element is the top. We follow the boolean intuition here, treating
. This awkwardness is due to a legacy problem. In the boolean intuition the most informative element is the bottom, where in the interpretation-ordering the most informative element is the top. We follow the boolean intuition here, treating ![]() as a kind of disjunction of theories and
as a kind of disjunction of theories and ![]() as a kind of conjunction.
as a kind of conjunction.
4 Certified extension
We prove Theorem 2.9. Our proof is based on the ideas from [Reference Visser22], but we exclude from the proof the use of
![]() $\sigma ^\star $
and interpretability.
$\sigma ^\star $
and interpretability.
Let
![]() $x < y$
be an abbreviation of
$x < y$
be an abbreviation of
![]() $x \leqslant y \land x \neq y$
. We define certain special elements as follows.
$x \leqslant y \land x \neq y$
. We define certain special elements as follows.
Definition 4.1 (Certification)
An element v is certified, or
![]() $\mathsf {cert}(v)$
, if it satisfies the following formulas. These formulas together form the certificate.
$\mathsf {cert}(v)$
, if it satisfies the following formulas. These formulas together form the certificate.
-
 $\mathsf {A}$
1.
$\mathsf {A}$
1.
 $0 \leqslant v$
$0 \leqslant v$
-
 $\mathsf {A}$
2.
$\mathsf {A}$
2.
 $\forall x < v\;\; \mathsf {s}\hspace{0.02cm} x \leqslant v$
$\forall x < v\;\; \mathsf {s}\hspace{0.02cm} x \leqslant v$
-
 $\mathsf {A}$
3.
$\mathsf {A}$
3.
 $\forall x \, (x\leqslant 0 \leftrightarrow x = 0)$
$\forall x \, (x\leqslant 0 \leftrightarrow x = 0)$
-
 $\mathsf {A}$
4.
$\mathsf {A}$
4.
 $\forall x \mathbin {<} v\, \forall y\, (y\leqslant \mathsf {s}\hspace{0.02cm} x \leftrightarrow (y \leqslant x \vee y=\mathsf {s}\hspace{0.02cm} x))$
$\forall x \mathbin {<} v\, \forall y\, (y\leqslant \mathsf {s}\hspace{0.02cm} x \leftrightarrow (y \leqslant x \vee y=\mathsf {s}\hspace{0.02cm} x))$
-
 $\mathsf {A}$
5.
$\mathsf {A}$
5.
 $\forall x, y, z \mathbin {\leqslant } v\,\; \mathsf {s}\hspace{0.01cm}((x \times y) + z) \neq 0$
$\forall x, y, z \mathbin {\leqslant } v\,\; \mathsf {s}\hspace{0.01cm}((x \times y) + z) \neq 0$
-
 $\mathsf {A}$
6.
$\mathsf {A}$
6.
 $\forall x, y, z, w \mathbin {\leqslant } v\,\; \mathsf {s}\hspace{0.01cm}((x \times y) + z) = \mathsf {s}\hspace{0.02cm} w \to (x \times y) + z = w$
$\forall x, y, z, w \mathbin {\leqslant } v\,\; \mathsf {s}\hspace{0.01cm}((x \times y) + z) = \mathsf {s}\hspace{0.02cm} w \to (x \times y) + z = w$
-
 $\mathsf {A}$
7.
$\mathsf {A}$
7.
 $\forall x, y \mathbin {\leqslant } v\; (x \times y) + 0 = x \times y$
$\forall x, y \mathbin {\leqslant } v\; (x \times y) + 0 = x \times y$
-
 $\mathsf {A}$
8.
$\mathsf {A}$
8.
 $\forall x, y, z \mathbin {\leqslant } v\; (x \times y) + \mathsf {s}\hspace{0.02cm} z = \mathsf {s}\hspace{0.01cm}((x \times y) + z) $
$\forall x, y, z \mathbin {\leqslant } v\; (x \times y) + \mathsf {s}\hspace{0.02cm} z = \mathsf {s}\hspace{0.01cm}((x \times y) + z) $
-
 $\mathsf {A}$
9.
$\mathsf {A}$
9.
 $\forall x \mathbin {\leqslant } v\; x \times 0 = 0$
$\forall x \mathbin {\leqslant } v\; x \times 0 = 0$
-
 $\mathsf {A}$
10.
$\mathsf {A}$
10.
 $\forall x, y \mathbin {\leqslant } v\; x \times \mathsf {s}\hspace{0.02cm} y = (x \times y) + x$
$\forall x, y \mathbin {\leqslant } v\; x \times \mathsf {s}\hspace{0.02cm} y = (x \times y) + x$
We note that of the properties defining certification, only
![]() $\mathsf {A{3}}$
and
$\mathsf {A{3}}$
and
![]() $\mathsf {A{4}}$
are not prima facie
$\mathsf {A{4}}$
are not prima facie
![]() $\Delta _0$
. However, we can rewrite
$\Delta _0$
. However, we can rewrite
![]() $\mathsf {A{3}}$
as
$\mathsf {A{3}}$
as
![]() $ \forall x\leqslant 0 \; x = 0 \wedge 0 \leqslant 0$
and we can rewrite
$ \forall x\leqslant 0 \; x = 0 \wedge 0 \leqslant 0$
and we can rewrite
![]() $\mathsf {A{4}}$
as
$\mathsf {A{4}}$
as
So, modulo equivalence in predicate logic, certification is
![]() $\Delta _0$
.
$\Delta _0$
.
The properties
![]() $\mathsf {A{5}}$
–
$\mathsf {A{5}}$
–
![]() $\mathsf {A{8}}$
look a bit different from the usual axioms in certificates. Their specific form is needed to prove Lemma 4.8, which in its turn is needed to prove the negative atomic cases of Lemma 4.11.
$\mathsf {A{8}}$
look a bit different from the usual axioms in certificates. Their specific form is needed to prove Lemma 4.8, which in its turn is needed to prove the negative atomic cases of Lemma 4.11.
Remark 4.2. We aimed to keep our definition of certification reasonably simple. This has the advantage that it made clear that we can use a fairly light property. As we will see in Example 5.9, it is possible to add all kinds of convenient properties to certification that preserve our intended application. An example of such a property is linearity of
![]() $\leqslant $
below v.
$\leqslant $
below v.
We say that
![]() $\sigma $
is a pure 1-
$\sigma $
is a pure 1-
![]() $\Sigma _1$
-sentence if it is of the form
$\Sigma _1$
-sentence if it is of the form
![]() $\exists x\, \sigma _0(x)$
, where
$\exists x\, \sigma _0(x)$
, where
![]() $\sigma _0(x)$
is a pure
$\sigma _0(x)$
is a pure
![]() $\Delta _0$
-formula.
$\Delta _0$
-formula.
We strengthen Proposition 2.8 as follows.
Proposition 4.3. For any
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\lambda $
, a pure 1-
$\lambda $
, a pure 1-
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence ![]() satisfying the following conditions can be effectively found:
satisfying the following conditions can be effectively found:
-
1.
 ,
, -
2.
 is logically valid.
is logically valid.
Proof. Consider any
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\lambda $
. By Proposition 2.8, we can effectively find a pure
$\lambda $
. By Proposition 2.8, we can effectively find a pure
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() ${\lambda }^{\circ }$
such that
${\lambda }^{\circ }$
such that
![]() $\mathbb {N} \models \lambda \leftrightarrow \lambda ^{\circ }$
and
$\mathbb {N} \models \lambda \leftrightarrow \lambda ^{\circ }$
and
![]() $\vdash \lambda ^{\circ } \to \lambda $
. Suppose that
$\vdash \lambda ^{\circ } \to \lambda $
. Suppose that
![]() $\lambda ^{\circ }$
is of the form
$\lambda ^{\circ }$
is of the form
![]() $\exists \vec {v}\, \lambda _0(\vec {v})$
for some pure
$\exists \vec {v}\, \lambda _0(\vec {v})$
for some pure
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\lambda _0(\vec {v})$
. Define
$\lambda _0(\vec {v})$
. Define ![]() to be the pure 1-
to be the pure 1-
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\exists x\, \exists \vec {v} \leqslant x\, \lambda _0(\vec {v})$
. Then,
$\exists x\, \exists \vec {v} \leqslant x\, \lambda _0(\vec {v})$
. Then, ![]() satisfies the conditions (1) and (2).
satisfies the conditions (1) and (2).
We are now ready to define certified
![]() $\Sigma _1$
-sentences.
$\Sigma _1$
-sentences.
Definition 4.4. Let
![]() $\sigma $
be a pure 1-
$\sigma $
be a pure 1-
![]() $\Sigma _1$
-sentence of the form
$\Sigma _1$
-sentence of the form
![]() $\exists x\, \sigma _0(x)$
. We define:
$\exists x\, \sigma _0(x)$
. We define:
The following theorem is the heart of the technical part of our results.
Theorem 4.5. Let
![]() $\sigma $
be a pure 1-
$\sigma $
be a pure 1-
![]() $\Sigma _1$
-sentence. Then:
$\Sigma _1$
-sentence. Then:
-
1.
 $\sigma ^{\mathsf {cert}} \vdash \sigma $
.
$\sigma ^{\mathsf {cert}} \vdash \sigma $
. -
2. If
 $\mathbb {N} \models \sigma $
, then
$\mathbb {N} \models \sigma $
, then
 $\mathsf {R}_0 \vdash \sigma ^{\mathsf {cert}}$
.
$\mathsf {R}_0 \vdash \sigma ^{\mathsf {cert}}$
. -
3. If
 $\mathbb {N} \models \neg \, \sigma $
, then
$\mathbb {N} \models \neg \, \sigma $
, then
 $\sigma ^{\mathsf {cert}} \vdash \mathsf {R}_0$
.
$\sigma ^{\mathsf {cert}} \vdash \mathsf {R}_0$
.
For each
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\lambda $
, we may define
$\lambda $
, we may define
![]() $[\lambda ]$
to be the sentence
$[\lambda ]$
to be the sentence ![]() . Then, Theorem 2.9 immediately follows from Theorem 4.5 and Proposition 4.3.
. Then, Theorem 2.9 immediately follows from Theorem 4.5 and Proposition 4.3.
Before proving Theorem 4.5, we investigate an
![]() $\mathbb {L}_{\mathsf {a}}$
-model
$\mathbb {L}_{\mathsf {a}}$
-model
![]() $\mathcal {M}$
. We assume that
$\mathcal {M}$
. We assume that
-
(†) :
 ${\mathfrak v}$
is a designated certified element and k is a natural number such that, for all
${\mathfrak v}$
is a designated certified element and k is a natural number such that, for all
 $m < k$
, we have
$m < k$
, we have
 $\mathcal {M} \models \underline {m} \neq {\mathfrak v}$
.
$\mathcal {M} \models \underline {m} \neq {\mathfrak v}$
.
Our first lemma is concerned with successor.
Lemma 4.6 (†)
For each
![]() $m \leqslant k$
, we have
$m \leqslant k$
, we have
![]() $\mathcal {M} \models \underline {m} \leqslant {\mathfrak v}$
.
$\mathcal {M} \models \underline {m} \leqslant {\mathfrak v}$
.
Proof. We prove the lemma by induction on
![]() $m \leqslant k$
. For
$m \leqslant k$
. For
![]() $m = 0$
, we have
$m = 0$
, we have
![]() $\mathcal {M} \models 0 \leqslant {\mathfrak v}$
by
$\mathcal {M} \models 0 \leqslant {\mathfrak v}$
by
![]() $\mathsf {A{1}}$
. Suppose that the lemma holds for m with
$\mathsf {A{1}}$
. Suppose that the lemma holds for m with
![]() $m + 1 \leqslant k$
. Then,
$m + 1 \leqslant k$
. Then,
![]() $\mathcal {M} \models \underline {m} \leqslant {\mathfrak v}$
by the induction hypothesis. Since
$\mathcal {M} \models \underline {m} \leqslant {\mathfrak v}$
by the induction hypothesis. Since
![]() $m< k$
and, hence, by Assumption (†),
$m< k$
and, hence, by Assumption (†),
![]() $\mathcal {M} \models \underline {m} \neq {\mathfrak v}$
, we find
$\mathcal {M} \models \underline {m} \neq {\mathfrak v}$
, we find
![]() $\mathcal {M} \models \underline {m} < {\mathfrak v}$
. So, by
$\mathcal {M} \models \underline {m} < {\mathfrak v}$
. So, by
![]() $\mathsf {A{2}}$
, we may conclude that
$\mathsf {A{2}}$
, we may conclude that
![]() $\mathcal {M} \models \underline {m+1} \leqslant {\mathfrak v}$
.
$\mathcal {M} \models \underline {m+1} \leqslant {\mathfrak v}$
.
In the proofs of the following lemmas, we will use Lemma 4.6 without any reference.
Lemma 4.7 (†)
For any
![]() $m \leqslant k$
, we have
$m \leqslant k$
, we have
 $\displaystyle \mathcal {M} \models \forall y\; \Bigl (y \leqslant \underline {m} \leftrightarrow \bigvee _{l \leqslant m} y = \underline {l} \Bigr )$
.
$\displaystyle \mathcal {M} \models \forall y\; \Bigl (y \leqslant \underline {m} \leftrightarrow \bigvee _{l \leqslant m} y = \underline {l} \Bigr )$
.
Proof. We prove our lemma by induction on
![]() $m\leqslant k$
. The case
$m\leqslant k$
. The case
![]() $m=0$
is precisely
$m=0$
is precisely
![]() $\mathsf {A{3}}$
. Suppose we have our equivalence for m with
$\mathsf {A{3}}$
. Suppose we have our equivalence for m with
![]() $m+1 \leqslant k$
. We note that
$m+1 \leqslant k$
. We note that
![]() $m<k$
, and hence
$m<k$
, and hence
![]() $\mathcal {M} \models \underline {m} < {\mathfrak v}$
. Thus, we have, by
$\mathcal {M} \models \underline {m} < {\mathfrak v}$
. Thus, we have, by
![]() $\mathsf {A{4}}$
:
$\mathsf {A{4}}$
:
 $$ \begin{align*} \mathcal {M} \models y \leqslant \underline{m+1} & \;\,\leftrightarrow\;\, y \leqslant \mathsf{s}\hspace{0.02cm} \underline{m} \\ & \;\,\leftrightarrow\;\, y \leqslant \underline{m} \lor y = \mathsf{s}\hspace{0.02cm} \underline{m} \\ & \;\,\leftrightarrow\;\, \bigvee_{l \leqslant m} y = \underline{l} \lor y = \underline{m+1} \\ & \;\,\leftrightarrow\;\, \bigvee_{l \leqslant m+1} y = \underline{l}. \end{align*} $$
$$ \begin{align*} \mathcal {M} \models y \leqslant \underline{m+1} & \;\,\leftrightarrow\;\, y \leqslant \mathsf{s}\hspace{0.02cm} \underline{m} \\ & \;\,\leftrightarrow\;\, y \leqslant \underline{m} \lor y = \mathsf{s}\hspace{0.02cm} \underline{m} \\ & \;\,\leftrightarrow\;\, \bigvee_{l \leqslant m} y = \underline{l} \lor y = \underline{m+1} \\ & \;\,\leftrightarrow\;\, \bigvee_{l \leqslant m+1} y = \underline{l}. \end{align*} $$
Lemma 4.8 (†)
For any
![]() $m, n, p \leqslant k$
, we have
$m, n, p \leqslant k$
, we have
![]() $\mathcal {M} \models (\underline {m} \times \underline {n}) + \underline {p} = \underline {(m \times n) + p}$
.
$\mathcal {M} \models (\underline {m} \times \underline {n}) + \underline {p} = \underline {(m \times n) + p}$
.
Proof. We prove the lemma by induction on n. For
![]() $n = 0$
, we prove that
$n = 0$
, we prove that
![]() $\mathcal {M} {\kern-1.5pt}\models{\kern-1.5pt} (\underline {m} {\kern-1.5pt}\times{\kern-1.5pt} 0) {\kern-1.5pt}+{\kern-1.5pt} \underline {p} {\kern-1.5pt}={\kern-1.5pt} \underline {p}$
by induction on p. For
$\mathcal {M} {\kern-1.5pt}\models{\kern-1.5pt} (\underline {m} {\kern-1.5pt}\times{\kern-1.5pt} 0) {\kern-1.5pt}+{\kern-1.5pt} \underline {p} {\kern-1.5pt}={\kern-1.5pt} \underline {p}$
by induction on p. For
![]() $p {\kern-1.5pt}={\kern-1.5pt} 0$
, we see
$p {\kern-1.5pt}={\kern-1.5pt} 0$
, we see
![]() $\mathcal {M} {\kern-1.5pt}\models{\kern-1.5pt} (\underline {m} {\kern-1.5pt}\times{\kern-1.5pt} 0) {\kern-1.5pt}+{\kern-1.5pt} 0 {\kern-1.5pt}={\kern-1.5pt} \underline {m} {\kern-1.5pt}\times{\kern-1.5pt} 0$
holds by
$\mathcal {M} {\kern-1.5pt}\models{\kern-1.5pt} (\underline {m} {\kern-1.5pt}\times{\kern-1.5pt} 0) {\kern-1.5pt}+{\kern-1.5pt} 0 {\kern-1.5pt}={\kern-1.5pt} \underline {m} {\kern-1.5pt}\times{\kern-1.5pt} 0$
holds by
![]() $\mathsf {A{7}}$
. Since
$\mathsf {A{7}}$
. Since
![]() $\mathcal {M} \models \underline {m} \times 0 = 0$
by
$\mathcal {M} \models \underline {m} \times 0 = 0$
by
![]() $\mathsf {A{9}}$
, we obtain
$\mathsf {A{9}}$
, we obtain
![]() $\mathcal {M} \models (\underline {m} \times 0) + 0 = 0$
.
$\mathcal {M} \models (\underline {m} \times 0) + 0 = 0$
.
Suppose that the statement holds for p with
![]() $p + 1 \leqslant k$
. Then, by
$p + 1 \leqslant k$
. Then, by
![]() $\mathsf {A{8}}$
and the induction hypothesis for p, we get
$\mathsf {A{8}}$
and the induction hypothesis for p, we get
We have proved that the lemma holds for
![]() $n = 0$
.
$n = 0$
.
Suppose that the lemma holds for n with
![]() $n + 1 \leqslant k$
. We prove that
$n + 1 \leqslant k$
. We prove that
![]() $\mathcal {M} \models (\underline {m} \times (\underline {n+1})) + \underline {p} = \underline {(m \times (n+1)) + p}$
by induction on p. For
$\mathcal {M} \models (\underline {m} \times (\underline {n+1})) + \underline {p} = \underline {(m \times (n+1)) + p}$
by induction on p. For
![]() $p = 0$
, by
$p = 0$
, by
![]() $\mathsf {A{7}}$
,
$\mathsf {A{7}}$
,
![]() $\mathsf {A{10}}$
, and the induction hypothesis for n, using that
$\mathsf {A{10}}$
, and the induction hypothesis for n, using that
![]() $m\leqslant k$
,
$m\leqslant k$
,
 $$ \begin{align*} \mathcal {M} \models (\underline{m} \times (\underline{n+1})) + 0 & = \underline{m} \times \mathsf{s}\hspace{0.02cm} \underline{n} \\ & = (\underline{m} \times \underline{n}) + \underline{m}\\ & = \underline{(m \times n) + m} \\ & = \underline{(m \times (n+1)) + 0}. \end{align*} $$
$$ \begin{align*} \mathcal {M} \models (\underline{m} \times (\underline{n+1})) + 0 & = \underline{m} \times \mathsf{s}\hspace{0.02cm} \underline{n} \\ & = (\underline{m} \times \underline{n}) + \underline{m}\\ & = \underline{(m \times n) + m} \\ & = \underline{(m \times (n+1)) + 0}. \end{align*} $$
Assume that the statement holds for p with
![]() $p + 1 \leqslant k$
. By
$p + 1 \leqslant k$
. By
![]() $\mathsf {A{8}}$
and the induction hypothesis for p,
$\mathsf {A{8}}$
and the induction hypothesis for p,
 $$ \begin{align*} \mathcal {M} \models (\underline{m} \times (\underline{n+1})) + (\underline{p+1}) & = (\underline{m} \times (\underline{n+1})) + \mathsf{s}\hspace{0.02cm} \underline{p}\\ &= \mathsf{s}\hspace{0.01cm}((\underline{m} \times (\underline{n+1})) + \underline{p})\\ & = \mathsf{s}\hspace{0.01cm}((\underline{m \times (n+1)) + p})\\ &= \underline{(m \times (n+1)) + (p+1)}. \end{align*} $$
$$ \begin{align*} \mathcal {M} \models (\underline{m} \times (\underline{n+1})) + (\underline{p+1}) & = (\underline{m} \times (\underline{n+1})) + \mathsf{s}\hspace{0.02cm} \underline{p}\\ &= \mathsf{s}\hspace{0.01cm}((\underline{m} \times (\underline{n+1})) + \underline{p})\\ & = \mathsf{s}\hspace{0.01cm}((\underline{m \times (n+1)) + p})\\ &= \underline{(m \times (n+1)) + (p+1)}. \end{align*} $$
Lemma 4.9 (†)
Let
![]() $m, n \leqslant k$
.
$m, n \leqslant k$
.
-
1.
 $\mathcal {M} \models \underline {m} \times \underline {n} = \underline {m \times n}$
,
$\mathcal {M} \models \underline {m} \times \underline {n} = \underline {m \times n}$
, -
2.
 $\mathcal {M} \models \underline {m} + \underline {n} = \underline {m + n}$
.
$\mathcal {M} \models \underline {m} + \underline {n} = \underline {m + n}$
.
Proof. 1. By Lemma 4.8, we get
![]() $\mathcal {M} \models (\underline {m} \times \underline {n}) + 0 = \underline {m \times n}$
. By
$\mathcal {M} \models (\underline {m} \times \underline {n}) + 0 = \underline {m \times n}$
. By
![]() $\mathsf {A{7}}$
, we obtain
$\mathsf {A{7}}$
, we obtain
![]() $\mathcal {M} \models \underline {m} \times \underline {n} = \underline {m \times n}$
.
$\mathcal {M} \models \underline {m} \times \underline {n} = \underline {m \times n}$
.
2. If
![]() $k = 0$
, then
$k = 0$
, then
![]() $m = n = 0$
. By
$m = n = 0$
. By
![]() $\mathsf {A{7}}$
,
$\mathsf {A{7}}$
,
![]() $\mathcal {M} \models (0 \times 0) + 0 = 0 \times 0$
. Since
$\mathcal {M} \models (0 \times 0) + 0 = 0 \times 0$
. Since
![]() $\mathcal {M} \models 0 \times 0 = 0$
by
$\mathcal {M} \models 0 \times 0 = 0$
by
![]() $\mathsf {A{9}}$
, we obtain
$\mathsf {A{9}}$
, we obtain
![]() $\mathcal {M} \models 0 + 0 = 0$
.
$\mathcal {M} \models 0 + 0 = 0$
.
If
![]() $k \geq 1$
, then by Lemma 4.8 and Clause 1, we obtain
$k \geq 1$
, then by Lemma 4.8 and Clause 1, we obtain
Lemma 4.10 (†)
Suppose
![]() $m \leqslant k^2+k$
and
$m \leqslant k^2+k$
and
![]() $l\leqslant k$
and
$l\leqslant k$
and
![]() $m\neq l$
. Then,
$m\neq l$
. Then,
![]() $\mathcal {M} \models \underline {m} \neq \underline {l}$
.
$\mathcal {M} \models \underline {m} \neq \underline {l}$
.
Proof. We prove our result by induction on
![]() $l\leqslant k$
. We will use the fact that (‡) every
$l\leqslant k$
. We will use the fact that (‡) every
![]() $m\leqslant k^2+k$
, can be written as
$m\leqslant k^2+k$
, can be written as
![]() $(k\times m_0)+m_1$
for some
$(k\times m_0)+m_1$
for some
![]() $m_0,m_1\leqslant k$
.
$m_0,m_1\leqslant k$
.
For the base case, suppose
![]() $l =0$
,
$l =0$
,
![]() $m \leqslant k^2+k$
, and
$m \leqslant k^2+k$
, and
![]() $m\neq l$
. We have
$m\neq l$
. We have
![]() $m = m'+1$
, so
$m = m'+1$
, so
![]() $\underline {m} = \mathsf {s}\hspace{0.02cm} \underline {m'}$
. So we are done by
$\underline {m} = \mathsf {s}\hspace{0.02cm} \underline {m'}$
. So we are done by
![]() $\mathsf {A{5}}$
in combination with (‡) and Lemma 4.8.
$\mathsf {A{5}}$
in combination with (‡) and Lemma 4.8.
We treat the successor case. Suppose
![]() $l= l'+1$
and we have the desired result for
$l= l'+1$
and we have the desired result for
![]() $l'$
. Suppose also
$l'$
. Suppose also
![]() $m \leqslant k^2+k$
, and
$m \leqslant k^2+k$
, and
![]() $m\neq l$
. In case
$m\neq l$
. In case
![]() $m=0$
, we are done by
$m=0$
, we are done by
![]() $\mathsf {A{5}}$
in combination with (‡) and Lemma 4.8. Suppose,
$\mathsf {A{5}}$
in combination with (‡) and Lemma 4.8. Suppose,
![]() $m= ((k\times m_0)+m_1)+1$
, where
$m= ((k\times m_0)+m_1)+1$
, where
![]() $m_0,m_1\leqslant k$
. Suppose
$m_0,m_1\leqslant k$
. Suppose
![]() $\mathcal {M} \models \underline {m} = \underline {l}$
. Then, by Lemma 4.8, we find
$\mathcal {M} \models \underline {m} = \underline {l}$
. Then, by Lemma 4.8, we find
![]() $\mathcal {M} \models \mathsf {s}\hspace{0.02cm} ((\underline {k}\times \underline {m_0})+\underline {m_1}) = \mathsf {s}\hspace{0.02cm} \underline {l'}$
. By
$\mathcal {M} \models \mathsf {s}\hspace{0.02cm} ((\underline {k}\times \underline {m_0})+\underline {m_1}) = \mathsf {s}\hspace{0.02cm} \underline {l'}$
. By
![]() $\mathsf {A{6}}$
, we may conclude
$\mathsf {A{6}}$
, we may conclude
![]() $\mathcal {M} \models (\underline {k}\times \underline {m_0})+\underline {m_1} = \underline {l'}$
. But this contradicts the induction hypothesis.
$\mathcal {M} \models (\underline {k}\times \underline {m_0})+\underline {m_1} = \underline {l'}$
. But this contradicts the induction hypothesis.
Lemma 4.11 (†)
For any pure
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (x_0, \ldots , x_{i})$
, and
$\varphi (x_0, \ldots , x_{i})$
, and
![]() $n_0, \ldots , n_{i} \leqslant k$
, if
$n_0, \ldots , n_{i} \leqslant k$
, if
![]() $\mathbb {N} \models \varphi (\underline {n_0}, \ldots , \underline {n_i})$
, then
$\mathbb {N} \models \varphi (\underline {n_0}, \ldots , \underline {n_i})$
, then
![]() $\mathcal {M} \models \varphi (\underline {n_0}, \ldots , \underline {n_i})$
.
$\mathcal {M} \models \varphi (\underline {n_0}, \ldots , \underline {n_i})$
.
Proof. For any pure
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\varphi (x_0, \ldots , x_{i})$
, and
$\varphi (x_0, \ldots , x_{i})$
, and
![]() $n_0, \ldots , n_{i} \leqslant k$
, we simultaneously prove the following two clauses by induction on the construction of
$n_0, \ldots , n_{i} \leqslant k$
, we simultaneously prove the following two clauses by induction on the construction of
![]() $\varphi $
:
$\varphi $
:
-
1. if
 $\mathbb {N} \models \varphi (\underline {n_0}, \ldots , \underline {n_i})$
, then
$\mathbb {N} \models \varphi (\underline {n_0}, \ldots , \underline {n_i})$
, then
 $\mathcal {M} \models \varphi (\underline {n_0}, \ldots , \underline {n_i})$
,
$\mathcal {M} \models \varphi (\underline {n_0}, \ldots , \underline {n_i})$
, -
2. if
 $\mathbb {N} \models \neg \, \varphi (\underline {n_0}, \ldots , \underline {n_i})$
, then
$\mathbb {N} \models \neg \, \varphi (\underline {n_0}, \ldots , \underline {n_i})$
, then
 $\mathcal {M} \models \neg \, \varphi (\underline {n_0}, \ldots , \underline {n_i})$
.
$\mathcal {M} \models \neg \, \varphi (\underline {n_0}, \ldots , \underline {n_i})$
.
Firstly, we prove that the statement holds for atomic formulas. We distinguish the following cases.
-
•
 $\varphi $
is of the form
$\varphi $
is of the form
 $x_0 = x_1$
.
$x_0 = x_1$
.1. If
 $\mathbb {N} \models \underline {n_0} = \underline {n_1}$
, then
$\mathbb {N} \models \underline {n_0} = \underline {n_1}$
, then
 $n_0 = n_1$
, and hence
$n_0 = n_1$
, and hence
 $\mathcal {M} \models \underline {n_0} = \underline {n_1}$
.
$\mathcal {M} \models \underline {n_0} = \underline {n_1}$
.2. If
 $\mathbb {N} \models \underline {n_0} \neq \underline {n_1}$
, then
$\mathbb {N} \models \underline {n_0} \neq \underline {n_1}$
, then
 $n_0 \neq n_1$
. By Lemma 4.10,
$n_0 \neq n_1$
. By Lemma 4.10,
 $\mathcal {M} \models \underline {n_0} \neq \underline {n_1}$
because
$\mathcal {M} \models \underline {n_0} \neq \underline {n_1}$
because
 $n_0, n_1 \leqslant k$
.
$n_0, n_1 \leqslant k$
. -
•
 $\varphi $
is of the form
$\varphi $
is of the form
 $0 = x_0$
.
$0 = x_0$
.1. If
 $\mathbb {N} \models 0 = \underline {n_0}$
, then
$\mathbb {N} \models 0 = \underline {n_0}$
, then
 $0 = n_0$
, and hence
$0 = n_0$
, and hence
 $\mathcal {M} \models 0 = \underline {n_0}$
.
$\mathcal {M} \models 0 = \underline {n_0}$
.2. If
 $\mathbb {N} \models 0 \neq \underline {n_0}$
, then
$\mathbb {N} \models 0 \neq \underline {n_0}$
, then
 $0 \neq n_0$
. By Lemma 4.10,
$0 \neq n_0$
. By Lemma 4.10,
 $\mathcal {M} \models 0 \neq \underline {n_0}$
because
$\mathcal {M} \models 0 \neq \underline {n_0}$
because
 $n_0 \leqslant k$
.
$n_0 \leqslant k$
. -
•
 $\varphi $
is of the form
$\varphi $
is of the form
 $\mathsf {s}\hspace{0.02cm} x_0 = x_1$
.
$\mathsf {s}\hspace{0.02cm} x_0 = x_1$
.1. If
 $\mathbb {N} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} = \underline {n_1}$
, then
$\mathbb {N} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} = \underline {n_1}$
, then
 $n_0 + 1 = n_1$
, and
$n_0 + 1 = n_1$
, and
 $\mathcal {M} \models \underline {n_0 + 1} = \underline {n_1}$
. This means
$\mathcal {M} \models \underline {n_0 + 1} = \underline {n_1}$
. This means
 $\mathcal {M} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} = \underline {n_1}$
.
$\mathcal {M} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} = \underline {n_1}$
.2. If
 $\mathbb {N} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} \neq \underline {n_1}$
, then
$\mathbb {N} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} \neq \underline {n_1}$
, then
 $n_0 + 1 \neq n_1$
. If
$n_0 + 1 \neq n_1$
. If
 $k = 0$
, then
$k = 0$
, then
 $n_0 = n_1 = 0$
. By
$n_0 = n_1 = 0$
. By
 $\mathsf {A{5}}$
, we get
$\mathsf {A{5}}$
, we get
 $\mathcal {M} \models \mathsf {s}\hspace{0.01cm}((0 \times 0) + 0) \neq 0$
. By Lemma 4.8,
$\mathcal {M} \models \mathsf {s}\hspace{0.01cm}((0 \times 0) + 0) \neq 0$
. By Lemma 4.8,
 $\mathcal {M} \models (0 \times 0) + 0 = 0$
, and hence
$\mathcal {M} \models (0 \times 0) + 0 = 0$
, and hence
 $\mathcal {M} \models \underline {1} \neq 0$
. This means
$\mathcal {M} \models \underline {1} \neq 0$
. This means
 $\mathcal {M} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} \neq \underline {n_1}$
. If
$\mathcal {M} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} \neq \underline {n_1}$
. If
 $k \geq 1$
, then
$k \geq 1$
, then
 $n_0 + 1 \leqslant k^2 + k$
. By Lemma 4.10, we have
$n_0 + 1 \leqslant k^2 + k$
. By Lemma 4.10, we have
 $\mathcal {M} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} \neq \underline {n_1}$
.
$\mathcal {M} \models \mathsf {s}\hspace{0.02cm} \underline {n_0} \neq \underline {n_1}$
. -
•
 $\varphi $
is of the form
$\varphi $
is of the form
 $x_0 + x_1 = x_2$
.
$x_0 + x_1 = x_2$
.1. If
 $\mathbb {N} \models \underline {n_0} + \underline {n_1} = \underline {n_2}$
, then
$\mathbb {N} \models \underline {n_0} + \underline {n_1} = \underline {n_2}$
, then
 $n_0 + n_1 = n_2$
, and
$n_0 + n_1 = n_2$
, and
 $\mathcal {M} \models \underline {n_0 + n_1} = \underline {n_2}$
. By Lemma 4.9,
$\mathcal {M} \models \underline {n_0 + n_1} = \underline {n_2}$
. By Lemma 4.9,
 $\mathcal {M} \models \underline {n_0} + \underline {n_1} = \underline {n_2}$
because
$\mathcal {M} \models \underline {n_0} + \underline {n_1} = \underline {n_2}$
because
 $n_0, n_1 \leqslant k$
.
$n_0, n_1 \leqslant k$
.2. If
 $\mathbb {N} \models \underline {n_0} + \underline {n_1} \neq \underline {n_2}$
, then
$\mathbb {N} \models \underline {n_0} + \underline {n_1} \neq \underline {n_2}$
, then
 $n_0 + n_1 \neq n_2$
. Since
$n_0 + n_1 \neq n_2$
. Since
 $n_0 + n_1 \leqslant k^2 + k$
and
$n_0 + n_1 \leqslant k^2 + k$
and
 $n_2 \leqslant k$
, by Lemma 4.10, we have
$n_2 \leqslant k$
, by Lemma 4.10, we have
 $\mathcal {M} \models \underline {n_0 + n_1} \neq \underline {n_2}$
. By Lemma 4.9, we have
$\mathcal {M} \models \underline {n_0 + n_1} \neq \underline {n_2}$
. By Lemma 4.9, we have
 $\mathcal {M} \models \underline {n_0} + \underline {n_1} \neq \underline {n_2}$
.
$\mathcal {M} \models \underline {n_0} + \underline {n_1} \neq \underline {n_2}$
. -
•
 $\varphi $
is of the form
$\varphi $
is of the form
 $x_0 \times x_1 = x_2$
.
$x_0 \times x_1 = x_2$
.1. If
 $\mathbb {N} \models \underline {n_0} \times \underline {n_1} = \underline {n_2}$
, then
$\mathbb {N} \models \underline {n_0} \times \underline {n_1} = \underline {n_2}$
, then
 $n_0 \times n_1 = n_2$
, and
$n_0 \times n_1 = n_2$
, and
 $\mathcal {M} \models \underline {n_0 \times n_1} = \underline {n_2}$
. By Lemma 4.9,
$\mathcal {M} \models \underline {n_0 \times n_1} = \underline {n_2}$
. By Lemma 4.9,
 $\mathcal {M} \models \underline {n_0} \times \underline {n_1} = \underline {n_2}$
because
$\mathcal {M} \models \underline {n_0} \times \underline {n_1} = \underline {n_2}$
because
 $n_0, n_1 \leqslant k$
.
$n_0, n_1 \leqslant k$
.2. If
 $\mathbb {N} \models \underline {n_0} \times \underline {n_1} \neq \underline {n_2}$
, then
$\mathbb {N} \models \underline {n_0} \times \underline {n_1} \neq \underline {n_2}$
, then
 $n_0 \times n_1 \neq n_2$
. By Lemma 4.10,
$n_0 \times n_1 \neq n_2$
. By Lemma 4.10,
 $\mathcal {M} \models \underline {n_0 \times n_1} \neq \underline {n_2}$
because
$\mathcal {M} \models \underline {n_0 \times n_1} \neq \underline {n_2}$
because
 $n_0 \times n_1 \leqslant k^2 + k$
and
$n_0 \times n_1 \leqslant k^2 + k$
and
 $n_2 \leqslant k$
. By Lemma 4.9,
$n_2 \leqslant k$
. By Lemma 4.9,
 $\mathcal {M} \models \underline {n_0} \times \underline {n_1} \neq \underline {n_2}$
.
$\mathcal {M} \models \underline {n_0} \times \underline {n_1} \neq \underline {n_2}$
. -
•
 $\varphi $
is of the form
$\varphi $
is of the form
 $x_0 \leqslant x_1$
.
$x_0 \leqslant x_1$
.1. If
 $\mathbb {N} \models \underline {n_0} \leqslant \underline {n_1}$
, then
$\mathbb {N} \models \underline {n_0} \leqslant \underline {n_1}$
, then
 $n_0 \leqslant n_1$
. Since
$n_0 \leqslant n_1$
. Since
 $\mathcal {M} \models \bigvee _{l \leqslant n_1} \underline {n_0} = \underline {l}$
, we have, by Lemma 4.7,
$\mathcal {M} \models \bigvee _{l \leqslant n_1} \underline {n_0} = \underline {l}$
, we have, by Lemma 4.7,
 $\mathcal {M} \models \underline {n_0} \leqslant \underline {n_1}$
because
$\mathcal {M} \models \underline {n_0} \leqslant \underline {n_1}$
because
 $n_1 \leqslant k$
.
$n_1 \leqslant k$
.2. If
 $\mathbb {N} \models \underline {n_0} \not \leqslant \underline {n_1}$
, then
$\mathbb {N} \models \underline {n_0} \not \leqslant \underline {n_1}$
, then
 $n_1 < n_0$
. For each
$n_1 < n_0$
. For each
 $l \leqslant n_1$
, we have
$l \leqslant n_1$
, we have
 $n_0 \neq l$
. We have
$n_0 \neq l$
. We have
 $M \models n_0 \neq l$
by Lemma 4.10 because
$M \models n_0 \neq l$
by Lemma 4.10 because
 $n_0, l \leq k$
. Then,
$n_0, l \leq k$
. Then,
 $\mathcal {M} \models \bigwedge _{l \leqslant n_1} \underline {n_0} \neq \underline {l}$
. Since
$\mathcal {M} \models \bigwedge _{l \leqslant n_1} \underline {n_0} \neq \underline {l}$
. Since
 $n_1 \leqslant k$
, by Lemma 4.7, we have
$n_1 \leqslant k$
, by Lemma 4.7, we have
 $\mathcal {M} \models \underline {n_0} \not \leqslant \underline {n_1}$
.
$\mathcal {M} \models \underline {n_0} \not \leqslant \underline {n_1}$
.
Secondly, we prove the induction steps. The case that
![]() $\varphi $
is one of the forms
$\varphi $
is one of the forms
![]() $\neg \, \varphi _0$
and
$\neg \, \varphi _0$
and
![]() $\varphi _0 \ast \varphi _1$
for
$\varphi _0 \ast \varphi _1$
for
![]() $\ast \in \{\land , \lor , \to \}$
is easily shown by the induction hypothesis. It suffices to show the case that
$\ast \in \{\land , \lor , \to \}$
is easily shown by the induction hypothesis. It suffices to show the case that
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\exists y \leqslant x_j\, \varphi _0(x_0, \ldots , x_i, y)$
, where the claim holds for
$\exists y \leqslant x_j\, \varphi _0(x_0, \ldots , x_i, y)$
, where the claim holds for
![]() $\varphi _0$
. The case that
$\varphi _0$
. The case that
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\forall y \leqslant x_j\, \varphi _0(x_0, \ldots , x_i, y)$
is proved similarly.
$\forall y \leqslant x_j\, \varphi _0(x_0, \ldots , x_i, y)$
is proved similarly.
1. Suppose
![]() $\mathbb {N} \models \exists y \mathbin {\leqslant } \underline {n_j}\; \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
. Then, there exists an
$\mathbb {N} \models \exists y \mathbin {\leqslant } \underline {n_j}\; \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
. Then, there exists an
![]() $n_{i+1}$
such that
$n_{i+1}$
such that
![]() $n_{i+1} \leq n_j \leq k$
and
$n_{i+1} \leq n_j \leq k$
and
![]() $\mathbb {N} \models \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, \underline {n_{i+1}})$
. By the induction hypothesis,
$\mathbb {N} \models \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, \underline {n_{i+1}})$
. By the induction hypothesis,
![]() $\mathcal {M} \models \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, \underline {n_{i+1}})$
. Also, we have already proved
$\mathcal {M} \models \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, \underline {n_{i+1}})$
. Also, we have already proved
![]() $\mathcal {M} \models \underline {n_{i+1}} \leqslant \underline {n_j}$
. Therefore, we obtain
$\mathcal {M} \models \underline {n_{i+1}} \leqslant \underline {n_j}$
. Therefore, we obtain
![]() $\mathcal {M} \models \exists y \mathbin {\leqslant } \underline {n_j}\, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
.
$\mathcal {M} \models \exists y \mathbin {\leqslant } \underline {n_j}\, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
.
2. Suppose we have
![]() $\mathbb {N} \models \neg \, \exists y \mathbin {\leqslant } \underline {n_j}\, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
, or, equivalently, we have
$\mathbb {N} \models \neg \, \exists y \mathbin {\leqslant } \underline {n_j}\, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
, or, equivalently, we have
![]() $\mathbb {N} \models \forall y \mathbin {\leqslant } \underline {n_j}\, \neg \, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
. Then, we have
$\mathbb {N} \models \forall y \mathbin {\leqslant } \underline {n_j}\, \neg \, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
. Then, we have
![]() $\mathbb {N} \models \neg \, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, \underline {l})$
, for each
$\mathbb {N} \models \neg \, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, \underline {l})$
, for each
![]() $l \leqslant n_j$
. By the induction hypothesis, we have
$l \leqslant n_j$
. By the induction hypothesis, we have
![]() $\mathcal {M} \models \neg \, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, \underline {l})$
for each
$\mathcal {M} \models \neg \, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, \underline {l})$
for each
![]() $l \leqslant n_j$
. Thus,
$l \leqslant n_j$
. Thus,
 $$\begin{align*}\mathcal {M} \models \forall y \Bigl(\bigvee_{l \mathbin{\leqslant} n_j} y = \underline{l} \to \neg \, \varphi_0(\underline{n_0}, \ldots, \underline{n_i}, y) \Bigr).\end{align*}$$
$$\begin{align*}\mathcal {M} \models \forall y \Bigl(\bigvee_{l \mathbin{\leqslant} n_j} y = \underline{l} \to \neg \, \varphi_0(\underline{n_0}, \ldots, \underline{n_i}, y) \Bigr).\end{align*}$$
By Lemma 4.7, we obtain
![]() $\mathcal {M} \models \forall y \mathbin {\leqslant } \underline {n_j}\, \neg \, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
, and, hence,
$\mathcal {M} \models \forall y \mathbin {\leqslant } \underline {n_j}\, \neg \, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
, and, hence,
![]() $\mathcal {M} \models \neg \, \exists y \mathbin {\leqslant } \underline {n_j}\, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
.
$\mathcal {M} \models \neg \, \exists y \mathbin {\leqslant } \underline {n_j}\, \varphi _0(\underline {n_0}, \ldots , \underline {n_i}, y)$
.
We have finished our investigation of the model
![]() $\mathcal {M}$
. We prove one further lemma as a bridge between the conditions on
$\mathcal {M}$
. We prove one further lemma as a bridge between the conditions on
![]() $\mathcal {M}$
of the preceding lemmas and a false
$\mathcal {M}$
of the preceding lemmas and a false
![]() $\Sigma _1$
-sentence and, then, we are ready for the proof of Theorem 4.5.
$\Sigma _1$
-sentence and, then, we are ready for the proof of Theorem 4.5.
Lemma 4.12. Let
![]() $\sigma $
be a pure 1-
$\sigma $
be a pure 1-
![]() $\Sigma _1$
-sentence of the form
$\Sigma _1$
-sentence of the form
![]() $\exists x \, \sigma _0(x)$
, where
$\exists x \, \sigma _0(x)$
, where
![]() $\sigma _0(x)$
is a pure
$\sigma _0(x)$
is a pure
![]() $\Delta _0$
-formula. Suppose
$\Delta _0$
-formula. Suppose
![]() $\mathbb {N} \models \neg \,\sigma $
. Let
$\mathbb {N} \models \neg \,\sigma $
. Let
![]() $\mathcal {N}$
be an
$\mathcal {N}$
be an
![]() $\mathbb {L}_{\mathsf {a}}$
-model and
$\mathbb {L}_{\mathsf {a}}$
-model and
![]() ${\mathfrak v} \in \mathcal {N}$
be a witness of
${\mathfrak v} \in \mathcal {N}$
be a witness of
![]() $\sigma ^{\mathsf {cert}}$
in
$\sigma ^{\mathsf {cert}}$
in
![]() $\mathcal {N}$
, that is,
$\mathcal {N}$
, that is,
![]() $\mathcal {N} \models \mathsf {cert}({\mathfrak v}) \wedge \sigma _0({\mathfrak v})$
. Then
$\mathcal {N} \models \mathsf {cert}({\mathfrak v}) \wedge \sigma _0({\mathfrak v})$
. Then
![]() $\mathcal {N} \models \underline {m} < {\mathfrak v}$
, for every
$\mathcal {N} \models \underline {m} < {\mathfrak v}$
, for every
![]() $m\in \omega $
.
$m\in \omega $
.
Proof. Suppose
![]() $\mathbb {N} \models \neg \,\sigma $
and
$\mathbb {N} \models \neg \,\sigma $
and
![]() $\mathcal {N} \models \mathsf {cert}({\mathfrak v}) \wedge \sigma _0({\mathfrak v})$
.
$\mathcal {N} \models \mathsf {cert}({\mathfrak v}) \wedge \sigma _0({\mathfrak v})$
.
We first show that, for every
![]() $m \in \omega $
, we have
$m \in \omega $
, we have
![]() $\mathcal {N} \models \underline {m} \neq {\mathfrak v}$
. Suppose
$\mathcal {N} \models \underline {m} \neq {\mathfrak v}$
. Suppose
![]() $\mathcal {N} \models \underline {m} ={\mathfrak v}$
, for some
$\mathcal {N} \models \underline {m} ={\mathfrak v}$
, for some
![]() $m \in \omega $
. Let
$m \in \omega $
. Let
![]() $m^\star $
be the least such m. Then, the condition (†) holds for
$m^\star $
be the least such m. Then, the condition (†) holds for
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() ${\mathfrak v}$
, and
${\mathfrak v}$
, and
![]() $m^\star $
. Since
$m^\star $
. Since
![]() $\mathbb {N} \models \neg \, \sigma _0(\underline {m}^\star )$
, we have, by Lemma 4.11,
$\mathbb {N} \models \neg \, \sigma _0(\underline {m}^\star )$
, we have, by Lemma 4.11,
![]() $\mathcal {N} \models \neg \, \sigma _0(\underline {m}^\star )$
. But this is impossible.
$\mathcal {N} \models \neg \, \sigma _0(\underline {m}^\star )$
. But this is impossible.
Since, for every m, we have
![]() $\mathcal {M} \models \underline {m} \neq {\mathfrak v}$
, Lemma 4.6 gives us that, for every m, we have
$\mathcal {M} \models \underline {m} \neq {\mathfrak v}$
, Lemma 4.6 gives us that, for every m, we have
![]() $\mathcal {M} \models \underline {m} < {\mathfrak v}$
.
$\mathcal {M} \models \underline {m} < {\mathfrak v}$
.
We now prove Theorem 4.5.
Proof of Theorem 4.5
Ad 1: The implication from
![]() $\sigma ^{\mathsf {cert}}$
to
$\sigma ^{\mathsf {cert}}$
to
![]() $\sigma $
is immediate.
$\sigma $
is immediate.
Ad 2: It is obvious that
![]() $\mathbb {N} \models \forall v\, \mathsf {cert}(v)$
holds. Suppose
$\mathbb {N} \models \forall v\, \mathsf {cert}(v)$
holds. Suppose
![]() $\mathbb {N} \models \sigma $
. It follows that
$\mathbb {N} \models \sigma $
. It follows that
![]() $\mathbb {N} \models \sigma ^{\mathsf {cert}}$
. Since
$\mathbb {N} \models \sigma ^{\mathsf {cert}}$
. Since
![]() $\sigma ^{\mathsf {cert}}$
is
$\sigma ^{\mathsf {cert}}$
is
![]() $\Sigma _1$
, we have, by
$\Sigma _1$
, we have, by
![]() $\Sigma _1$
-completeness (Theorem 2.3), that
$\Sigma _1$
-completeness (Theorem 2.3), that
![]() $\mathsf {R}_0 \vdash \sigma ^{\mathsf {cert}}$
.
$\mathsf {R}_0 \vdash \sigma ^{\mathsf {cert}}$
.
Ad 3: Suppose
![]() $\mathbb {N} \models \neg \,\sigma $
. We prove that the theory
$\mathbb {N} \models \neg \,\sigma $
. We prove that the theory
![]() $\sigma ^{\mathsf {cert}}$
is
$\sigma ^{\mathsf {cert}}$
is
![]() $\Sigma _1$
-complete.
$\Sigma _1$
-complete.
Let
![]() $\mathcal {N}$
be any
$\mathcal {N}$
be any
![]() $\mathbb {L}_{\mathsf {a}}$
-model of
$\mathbb {L}_{\mathsf {a}}$
-model of
![]() $\sigma ^{\mathsf {cert}}$
. So, for some
$\sigma ^{\mathsf {cert}}$
. So, for some
![]() ${\mathfrak v}$
, we have
${\mathfrak v}$
, we have
![]() $\mathcal {N} \models \mathsf {cert}({\mathfrak v}) \wedge \sigma _0({\mathfrak v})$
. By Lemma 4.12, we find that
$\mathcal {N} \models \mathsf {cert}({\mathfrak v}) \wedge \sigma _0({\mathfrak v})$
. By Lemma 4.12, we find that
![]() $\mathcal {N} \models \underline {m} \neq {\mathfrak v}$
for every
$\mathcal {N} \models \underline {m} \neq {\mathfrak v}$
for every
![]() $m \in \omega $
. Hence, the condition (†) holds for
$m \in \omega $
. Hence, the condition (†) holds for
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() ${\mathfrak v}$
, and all
${\mathfrak v}$
, and all
![]() $k \in \omega $
.
$k \in \omega $
.
Let
![]() $\psi $
be any
$\psi $
be any
![]() $\Sigma _1$
-sentence such that
$\Sigma _1$
-sentence such that
![]() $\mathbb {N} \models \psi $
. By Proposition 4.3, there exists a pure
$\mathbb {N} \models \psi $
. By Proposition 4.3, there exists a pure
![]() $\Delta _0$
-formula
$\Delta _0$
-formula
![]() $\delta (x)$
satisfying the following conditions:
$\delta (x)$
satisfying the following conditions:
-
1.
 $\mathbb {N} \models \psi \leftrightarrow \exists x \, \delta (x)$
,
$\mathbb {N} \models \psi \leftrightarrow \exists x \, \delta (x)$
, -
2.
 $\exists x \, \delta (x) \to \psi $
is logically valid.
$\exists x \, \delta (x) \to \psi $
is logically valid.
Then,
![]() $\mathbb {N} \models \exists x \, \delta (x)$
, and, hence,
$\mathbb {N} \models \exists x \, \delta (x)$
, and, hence,
![]() $\mathbb {N} \models \delta (\underline {n})$
for some n. By Lemma 4.11, we have
$\mathbb {N} \models \delta (\underline {n})$
for some n. By Lemma 4.11, we have
![]() $\mathcal {N} \models \delta (\underline {n})$
. By the completeness theorem, we obtain
$\mathcal {N} \models \delta (\underline {n})$
. By the completeness theorem, we obtain
![]() $\sigma ^{\mathsf {cert}} \vdash \delta (\underline {n})$
.Footnote
2
Thus,
$\sigma ^{\mathsf {cert}} \vdash \delta (\underline {n})$
.Footnote
2
Thus,
![]() $\sigma ^{\mathsf {cert}} \vdash \exists x \, \delta (x)$
. Therefore, we obtain
$\sigma ^{\mathsf {cert}} \vdash \exists x \, \delta (x)$
. Therefore, we obtain
![]() $\sigma ^{\mathsf {cert}} \vdash \psi $
.
$\sigma ^{\mathsf {cert}} \vdash \psi $
.
Finally, by Theorem 2.3, we conclude that
![]() $\sigma ^{\mathsf {cert}} \vdash \mathsf {R}_0$
.
$\sigma ^{\mathsf {cert}} \vdash \mathsf {R}_0$
.
5 Certified extension generalized
In this section, we generalize Theorem 2.9 to a wide class of further base theories.
5.1 The theory
 $\mathsf {R}_{0\mathsf {p}}$
$\mathsf {R}_{0\mathsf {p}}$
We start with reproving Theorem 2.9 for a slightly different base theory. We define:
-
•
 $\mathbb {L}_{\mathsf {ap}}$
is the arithmetical signature
$\mathbb {L}_{\mathsf {ap}}$
is the arithmetical signature
 $\mathbb {L}_{\mathsf {a}}$
extended by a unary predicate symbol
$\mathbb {L}_{\mathsf {a}}$
extended by a unary predicate symbol
 $\mathsf {P}$
.
$\mathsf {P}$
. -
•
 $\mathfrak {id}_{\mathsf {ap}}:= \mathfrak {id}_{\mathbb {L}_{\mathsf {ap}}}$
. (The notion
$\mathfrak {id}_{\mathsf {ap}}:= \mathfrak {id}_{\mathbb {L}_{\mathsf {ap}}}$
. (The notion
 $\mathfrak {id}_{}$
is explained in Definition 3.1.)
$\mathfrak {id}_{}$
is explained in Definition 3.1.) -
•
 $\mathsf {R}_{0\mathsf {p}}$
is the the
$\mathsf {R}_{0\mathsf {p}}$
is the the
 $\mathbb {L}_{\mathsf {ap}}$
-theory obtained by extending
$\mathbb {L}_{\mathsf {ap}}$
-theory obtained by extending
 $\mathsf {R}_0$
with the axioms
$\mathsf {R}_0$
with the axioms
 $\mathsf {P}(\underline {n})$
, for all
$\mathsf {P}(\underline {n})$
, for all
 $n\in \omega $
.
$n\in \omega $
.
We have:
Theorem 5.1 (Second Certified Extension Theorem)
For each
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\sigma $
, we can effectively find a sentence
$\sigma $
, we can effectively find a sentence ![]() satisfying the following conditions:
satisfying the following conditions:
-
1.
 .
. -
2. If
 $\mathbb {N} \models \sigma $
, then
$\mathbb {N} \models \sigma $
, then  .
. -
3. If
 $\mathbb {N} \models \neg \, \sigma $
, then
$\mathbb {N} \models \neg \, \sigma $
, then  .
.
Proof. For each pure 1-
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\sigma $
, let
$\sigma $
, let
![]() $\sigma ^{\mathsf {cert_p}}$
be the
$\sigma ^{\mathsf {cert_p}}$
be the
![]() $\mathbb {L}_{\mathsf {a}}$
-sentence:
$\mathbb {L}_{\mathsf {a}}$
-sentence:
The proof of Theorem 4.5 can be repeated for
![]() $\mathsf {R}_{0\mathsf {p}}$
by using the sentence
$\mathsf {R}_{0\mathsf {p}}$
by using the sentence
![]() $\sigma ^{\mathsf {cert_p}}$
. Thus, for each
$\sigma ^{\mathsf {cert_p}}$
. Thus, for each
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\sigma $
, it is shown that
$\sigma $
, it is shown that ![]() satisfies the required conditions.
satisfies the required conditions.
The addition of
![]() $\bigwedge \mathfrak {id}_{\mathsf {ap}}$
in the definition of
$\bigwedge \mathfrak {id}_{\mathsf {ap}}$
in the definition of ![]() is superfluous in the context of the proof of Theorem 5.1. It is added since it also delivers the following simple insight.
is superfluous in the context of the proof of Theorem 5.1. It is added since it also delivers the following simple insight.
Theorem 5.2. Suppose
![]() $\tau $
is a translation from
$\tau $
is a translation from
![]() $\mathbb {L}_{\mathsf {ap}}$
to a signature of some theory. Let
$\mathbb {L}_{\mathsf {ap}}$
to a signature of some theory. Let
![]() $\sigma $
be a
$\sigma $
be a
![]() $\Sigma _1$
-sentence. Then,
$\Sigma _1$
-sentence. Then, ![]() , where
, where
![]() $\mathsf {K}_\tau $
is the interpretation based on
$\mathsf {K}_\tau $
is the interpretation based on
![]() $\tau $
.
$\tau $
.
5.2
 $\mathsf {R}_{0\mathsf {p}}$
-sourced theories
$\mathsf {R}_{0\mathsf {p}}$
-sourced theories
We define:
-
• Let T and U be c.e. theories and let
 $\varTheta $
be the signature of T. Let
$\varTheta $
be the signature of T. Let
 $\tau $
be a translation from
$\tau $
be a translation from
 $\varTheta $
to the U-signature. The theory U is
$\varTheta $
to the U-signature. The theory U is
 $\tau $
-T-sourced iff U is deductively equivalent to
$\tau $
-T-sourced iff U is deductively equivalent to
 $(T+ \mathfrak {id}_{\varTheta })^{\tau }$
. The theory U is T-sourced if it is
$(T+ \mathfrak {id}_{\varTheta })^{\tau }$
. The theory U is T-sourced if it is
 $\tau $
-T-sourced, for some
$\tau $
-T-sourced, for some
 $\tau $
.
$\tau $
.
In this paper we just focus on
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theories. We have:
$\mathsf {R}_{0\mathsf {p}}$
-sourced theories. We have:
Theorem 5.3 (Generalized certified extension theorem)
Suppose W is
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced. Then, for each
$\mathsf {R}_{0\mathsf {p}}$
-sourced. Then, for each
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\sigma $
, we can effectively find a sentence
$\sigma $
, we can effectively find a sentence ![]() satisfying the following conditions:
satisfying the following conditions:
-
1.
 .
. -
2. If
 $\mathbb {N} \models \sigma $
, then
$\mathbb {N} \models \sigma $
, then  .
. -
3. If
 $\mathbb {N} \models \neg \, \sigma $
, then
$\mathbb {N} \models \neg \, \sigma $
, then  .
.
Here is a first simple example of a
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theory.
$\mathsf {R}_{0\mathsf {p}}$
-sourced theory.
Example 5.4. Any finitely axiomatized theory A that interprets
![]() $\mathsf {R}_0$
is
$\mathsf {R}_0$
is
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced. We note that this example is not very useful, since we already know that the applications we want from
$\mathsf {R}_{0\mathsf {p}}$
-sourced. We note that this example is not very useful, since we already know that the applications we want from
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theories hold for finitely axiomatized theories.
$\mathsf {R}_{0\mathsf {p}}$
-sourced theories hold for finitely axiomatized theories.
Here is a second example. We remind the reader of Vaught’s set theory
![]() $\mathsf {VS}$
. It is a theory in the signature with the single binary relation symbol
$\mathsf {VS}$
. It is a theory in the signature with the single binary relation symbol
![]() $\in $
, axiomatized by the following axioms.
$\in $
, axiomatized by the following axioms.
-
 $\mathsf {VS}n$
:
$\mathsf {VS}n$
:
 $ \forall x_0 \dots \forall x_{n-1}\, \exists z\, \forall y \, (y \in z \leftrightarrow \bigvee _{i<n}y =x_i)$
$ \forall x_0 \dots \forall x_{n-1}\, \exists z\, \forall y \, (y \in z \leftrightarrow \bigvee _{i<n}y =x_i)$
We note that in the case that
![]() $n=0$
, we have an axiom that guarantees the existence of some empty sets. We have:
$n=0$
, we have an axiom that guarantees the existence of some empty sets. We have:
Theorem 5.5.
![]() $\mathsf {VS}$
interprets
$\mathsf {VS}$
interprets
![]() $\mathsf {R}_0$
.
$\mathsf {R}_0$
.
Proof. In [Reference Visser25, Appendix A], it was proven that
![]() $\mathsf {VS}$
interprets
$\mathsf {VS}$
interprets
![]() $\mathsf {R}$
. So, a fortiori,
$\mathsf {R}$
. So, a fortiori,
![]() $\mathsf {VS}$
interprets
$\mathsf {VS}$
interprets
![]() $\mathsf {R}_0$
.
$\mathsf {R}_0$
.
Theorem 5.6. The theory
![]() $\mathsf {VS}$
is
$\mathsf {VS}$
is
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced.
$\mathsf {R}_{0\mathsf {p}}$
-sourced.
The idea of the proof is to represent
![]() $\mathsf {VS}$
as Adjunctive Set Theory
$\mathsf {VS}$
as Adjunctive Set Theory
![]() $\mathsf {AS}$
with local size restrictions on the sets to which one can apply adjunction.
$\mathsf {AS}$
with local size restrictions on the sets to which one can apply adjunction.
Proof. Let
![]() $\nu $
be the translation on which an interpretation of
$\nu $
be the translation on which an interpretation of
![]() $\mathsf {R}_0$
in
$\mathsf {R}_0$
in
![]() $\mathsf {VS}$
is based. We assume that
$\mathsf {VS}$
is based. We assume that
![]() $\nu $
is one-dimensional—as the translation provided by [Reference Visser25] is. The many-dimensional case only requires minor adaptations.
$\nu $
is one-dimensional—as the translation provided by [Reference Visser25] is. The many-dimensional case only requires minor adaptations.
We extend
![]() $\nu $
to
$\nu $
to
![]() $\nu ^\star $
by providing a translation of
$\nu ^\star $
by providing a translation of
![]() $\mathsf {P}$
. The statement
$\mathsf {P}$
. The statement
![]() $\mathsf {P}_{\nu ^\star }( x)$
will roughly say that
$\mathsf {P}_{\nu ^\star }( x)$
will roughly say that
![]() $\mathsf {VS}0$
and
$\mathsf {VS}0$
and
![]() $\mathsf {VS}2$
and that, whenever we have a set y of cardinality
$\mathsf {VS}2$
and that, whenever we have a set y of cardinality
![]() $\leqslant x$
, we may adjoin any z to y. Here
$\leqslant x$
, we may adjoin any z to y. Here
![]() $\mathsf {VS}0$
and
$\mathsf {VS}0$
and
![]() $\mathsf {VS}2$
are needed to provide the necessary coding machinery. Here are the ingredients for formulation of our statement.
$\mathsf {VS}2$
are needed to provide the necessary coding machinery. Here are the ingredients for formulation of our statement.
-
• f is an injection from objects to numbers or
 $\mathsf {in}(f)$
iff f is a set of pairs, f is functional w.r.t.
$\mathsf {in}(f)$
iff f is a set of pairs, f is functional w.r.t.
 $=$
, the objects in the range of f are in
$=$
, the objects in the range of f are in
 $\delta _\nu $
, and f is injective in the sense that, if
$\delta _\nu $
, and f is injective in the sense that, if
 $f(u) =_\nu f(v)$
, then
$f(u) =_\nu f(v)$
, then
 $u=v$
.
$u=v$
. -
•
 $\mathsf {dom}(f,y)$
iff
$\mathsf {dom}(f,y)$
iff
 $\forall w\, (w\in y \leftrightarrow \exists v\, f(w)=v)$
.
$\forall w\, (w\in y \leftrightarrow \exists v\, f(w)=v)$
. -
•
 $\mathsf {card}_{\leqslant } (y,x)$
iff there is an f with
$\mathsf {card}_{\leqslant } (y,x)$
iff there is an f with
 $\mathsf {in}(f)$
and
$\mathsf {in}(f)$
and
 $\mathsf {dom}(f,y)$
and
$\mathsf {dom}(f,y)$
and
 $\forall v\in y\, f(v) <_\nu x $
.
$\forall v\in y\, f(v) <_\nu x $
. -
•
 $\mathsf {P}_{\nu ^\star }(x)$
iff
$\mathsf {P}_{\nu ^\star }(x)$
iff
 $\mathsf {VS}0$
and
$\mathsf {VS}0$
and
 $\mathsf {VS}2$
and
$\mathsf {VS}2$
and  $$\begin{align*}\forall y\, \forall z\, (\mathsf{card}_{\leqslant}(y,x) \to \exists w \, \forall u\, (u \in w \leftrightarrow (u\in x \vee u =z))).\end{align*}$$
$$\begin{align*}\forall y\, \forall z\, (\mathsf{card}_{\leqslant}(y,x) \to \exists w \, \forall u\, (u \in w \leftrightarrow (u\in x \vee u =z))).\end{align*}$$
The deductive equivalence between
![]() $\mathsf {R}^{\nu ^\star }_{0\mathsf {p}}$
and
$\mathsf {R}^{\nu ^\star }_{0\mathsf {p}}$
and
![]() $\mathsf {VS}$
is now easy to verify.
$\mathsf {VS}$
is now easy to verify.
We provide two larger classes of examples of
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theories. Consider any signature
$\mathsf {R}_{0\mathsf {p}}$
-sourced theories. Consider any signature
![]() $\mathcal {L}$
. Let
$\mathcal {L}$
. Let
![]() $\tau _0$
be a translation of
$\tau _0$
be a translation of
![]() $\mathcal {L}$
in
$\mathcal {L}$
in
![]() $\mathbb {L}_{\mathsf {a}}$
.
$\mathbb {L}_{\mathsf {a}}$
.
Let
![]() $\chi _0(x_0, \ldots , x_{k_0-1})$
, …,
$\chi _0(x_0, \ldots , x_{k_0-1})$
, …,
![]() $\chi _m(x_0, \ldots , x_{k_m-1})$
be any
$\chi _m(x_0, \ldots , x_{k_m-1})$
be any
![]() $\mathcal {L}$
-formulas and let
$\mathcal {L}$
-formulas and let
![]() $X_0, \ldots , X_m$
be any computable relations on
$X_0, \ldots , X_m$
be any computable relations on
![]() $\omega $
such that
$\omega $
such that
![]() $X_i \subseteq \omega ^{k_i}$
for each
$X_i \subseteq \omega ^{k_i}$
for each
![]() $i \leqslant m$
. We write
$i \leqslant m$
. We write
![]() $\underline {n}$
for the
$\underline {n}$
for the
![]() $\tau _0$
-numerals in the context of
$\tau _0$
-numerals in the context of
![]() $\mathcal {L}$
. We define the theory
$\mathcal {L}$
. We define the theory
![]() $\mathsf {R}_0[\tau _0;\chi _0, \ldots , \chi _m; X_0, \ldots , X_m]$
as follows:
$\mathsf {R}_0[\tau _0;\chi _0, \ldots , \chi _m; X_0, \ldots , X_m]$
as follows:
We use
![]() $\mathsf {R}_0[\tau _0;\vec {\chi }; \vec {X}]$
as an abbreviation of
$\mathsf {R}_0[\tau _0;\vec {\chi }; \vec {X}]$
as an abbreviation of
![]() $\mathsf {R}_0[\tau _0;\chi _0, \ldots , \chi _m; X_0, \ldots , X_m]$
. If
$\mathsf {R}_0[\tau _0;\chi _0, \ldots , \chi _m; X_0, \ldots , X_m]$
. If
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $\mathbb {L}_{\mathsf {a}}$
and if
$\mathbb {L}_{\mathsf {a}}$
and if
![]() $\tau _0$
is the identity translation on
$\tau _0$
is the identity translation on
![]() $\mathbb {L}_{\mathsf {a}}$
, we simply omit
$\mathbb {L}_{\mathsf {a}}$
, we simply omit
![]() $\tau _0$
.
$\tau _0$
.
Theorem 5.7. Let
![]() $\mathcal {L}$
be a signature, let
$\mathcal {L}$
be a signature, let
![]() $\tau _0$
be a translation of
$\tau _0$
be a translation of
![]() $\mathbb {L}_{\mathsf {a}}$
into
$\mathbb {L}_{\mathsf {a}}$
into
![]() $\mathcal {L}$
. Let
$\mathcal {L}$
. Let
![]() $\vec {\chi }$
be any
$\vec {\chi }$
be any
![]() $\mathcal {L}$
-formulas and let
$\mathcal {L}$
-formulas and let
![]() $\vec {X}$
be computable relations on
$\vec {X}$
be computable relations on
![]() $\omega $
matching
$\omega $
matching
![]() $\vec {\chi }$
. Then,
$\vec {\chi }$
. Then,
![]() $\mathsf {R}_0[\tau _0;\vec {\chi }; \vec {X}]$
is
$\mathsf {R}_0[\tau _0;\vec {\chi }; \vec {X}]$
is
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced.
$\mathsf {R}_{0\mathsf {p}}$
-sourced.
Proof. To simplify inessentially we assume that
![]() $\tau _0$
is 1-dimensional. For each
$\tau _0$
is 1-dimensional. For each
![]() $i \leqslant m$
, let
$i \leqslant m$
, let
![]() $\xi _i(x_0, \ldots , x_{k_i-1})$
be an
$\xi _i(x_0, \ldots , x_{k_i-1})$
be an
![]() $\mathbb {L}_{\mathsf {a}}$
-formula representing
$\mathbb {L}_{\mathsf {a}}$
-formula representing
![]() $X_i$
in
$X_i$
in
![]() $\mathsf {R}_0$
. That is, for any
$\mathsf {R}_0$
. That is, for any
![]() $n_0, \ldots , n_{k_i-1} \in \omega $
, if
$n_0, \ldots , n_{k_i-1} \in \omega $
, if
![]() $(n_0, \ldots , n_{k_i-1}) \in X_i$
, then
$(n_0, \ldots , n_{k_i-1}) \in X_i$
, then
![]() $\mathsf {R}_0 \vdash \xi _i(\underline {n_0}, \ldots , \underline {n_{k_i-1}})$
; and if
$\mathsf {R}_0 \vdash \xi _i(\underline {n_0}, \ldots , \underline {n_{k_i-1}})$
; and if
![]() $(n_0, \ldots , n_{k_i-1}) \notin X_i$
, then
$(n_0, \ldots , n_{k_i-1}) \notin X_i$
, then
![]() $\mathsf {R}_0 \vdash \neg \, \xi _i(\underline {n_0}, \ldots , \underline {n_{k_i-1}})$
. Let
$\mathsf {R}_0 \vdash \neg \, \xi _i(\underline {n_0}, \ldots , \underline {n_{k_i-1}})$
. Let
![]() $\chi ^*(x)$
be the
$\chi ^*(x)$
be the
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
We extend
![]() $\tau _0$
to
$\tau _0$
to
![]() $\tau $
by setting
$\tau $
by setting
![]() $\mathsf {P}_\tau (x) := \chi ^\ast (x)$
. Then, clearly,
$\mathsf {P}_\tau (x) := \chi ^\ast (x)$
. Then, clearly,
![]() $\mathsf {R}_0[\tau _0; \vec {\chi }; \vec {X}]$
is deductively equivalent to
$\mathsf {R}_0[\tau _0; \vec {\chi }; \vec {X}]$
is deductively equivalent to
![]() $\mathsf {R}_{0\mathsf {p}}^\tau $
.
$\mathsf {R}_{0\mathsf {p}}^\tau $
.
Example 5.8. The theory
![]() $\mathsf {R}_0$
is
$\mathsf {R}_0$
is
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced since it is deductively equivalent to
$\mathsf {R}_{0\mathsf {p}}$
-sourced since it is deductively equivalent to
![]() $\mathsf {R}_0[x=x; \emptyset ]$
and the theory
$\mathsf {R}_0[x=x; \emptyset ]$
and the theory
![]() $\mathsf {R}$
is
$\mathsf {R}$
is
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced since it is deductively equivalent to
$\mathsf {R}_{0\mathsf {p}}$
-sourced since it is deductively equivalent to
![]() $\mathsf {R}_0[\forall y\, (y \leqslant x \lor x \leqslant y); \omega ]$
.
$\mathsf {R}_0[\forall y\, (y \leqslant x \lor x \leqslant y); \omega ]$
.
Example 5.9. Suppose
![]() $\forall \vec {x}\, P_0(\vec {x})$
is a true pure
$\forall \vec {x}\, P_0(\vec {x})$
is a true pure
![]() $\Pi _1$
-sentence. Consider
$\Pi _1$
-sentence. Consider
![]() $W :=\mathsf {R}_0[P_0;\omega ^n]$
, where n is the length of
$W :=\mathsf {R}_0[P_0;\omega ^n]$
, where n is the length of
![]() $\vec {x}$
. Then, by
$\vec {x}$
. Then, by
![]() $\Sigma _1$
-completeness, W is deductively equivalent to
$\Sigma _1$
-completeness, W is deductively equivalent to
![]() $\mathsf {R}_0$
. However, modulo deductive equivalence, the corresponding
$\mathsf {R}_0$
. However, modulo deductive equivalence, the corresponding
![]() $(\sigma ^{\mathsf {cert_p}})^\tau $
has the form
$(\sigma ^{\mathsf {cert_p}})^\tau $
has the form
![]() $\exists z\, (\mathsf {cert}(z) \wedge \forall \vec {x} \mathbin {\leqslant } z\, P_0(\vec {x}) \wedge \exists z\, \sigma _0(z))$
. So, we may think of
$\exists z\, (\mathsf {cert}(z) \wedge \forall \vec {x} \mathbin {\leqslant } z\, P_0(\vec {x}) \wedge \exists z\, \sigma _0(z))$
. So, we may think of
![]() $\mathsf {cert}(z) \wedge \forall \vec {x} \mathbin {\leqslant } z\, P_0(\vec {x})$
as replacing
$\mathsf {cert}(z) \wedge \forall \vec {x} \mathbin {\leqslant } z\, P_0(\vec {x})$
as replacing
![]() $\mathsf {cert}(z)$
. Thus, we may add all kind of desirable properties to
$\mathsf {cert}(z)$
. Thus, we may add all kind of desirable properties to
![]() $\mathsf {cert}$
like the linearity of
$\mathsf {cert}$
like the linearity of
![]() $\leqslant $
below the certified element. This may be useful if we want to use certification as the basis of an interpretation of a stronger theory in
$\leqslant $
below the certified element. This may be useful if we want to use certification as the basis of an interpretation of a stronger theory in
![]() $\mathsf {R}_0$
.
$\mathsf {R}_0$
.
In the development below, we use the notion of depth-of-quantifier-alternations complexity, henceforth, simply complexity. For a careful exposition of this notion, see [Reference Visser24].
Theorem 5.10. Consider a finitely axiomatized theory A and a number n and a computable set X of A-sentences of complexity
![]() $\leqslant n$
. Suppose that:
$\leqslant n$
. Suppose that:
-
• A interprets
 $\mathsf {R}_0$
via an interpretation based on translation
$\mathsf {R}_0$
via an interpretation based on translation
 $\tau _0$
.
$\tau _0$
. -
• There is an A formula
 $\varPhi $
such that
$\varPhi $
such that
 $A \vdash \varPhi (\ulcorner {\phi }\urcorner ) \leftrightarrow \phi $
, for all A-sentences
$A \vdash \varPhi (\ulcorner {\phi }\urcorner ) \leftrightarrow \phi $
, for all A-sentences
 $\phi $
of complexity
$\phi $
of complexity
 $\leqslant n$
. Here the numerals are the
$\leqslant n$
. Here the numerals are the
 $\tau _0$
-numerals. (Note that these could be sequences modulo a definable equivalence relation.)
$\tau _0$
-numerals. (Note that these could be sequences modulo a definable equivalence relation.)
Then
![]() $A + X$
is an
$A + X$
is an
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory.
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory.
Proof. We write
![]() $\top $
for the non-empty zero-ary relationFootnote
3
and
$\top $
for the non-empty zero-ary relationFootnote
3
and
![]() $\bigwedge A$
for the sentence that is the conjunction of the axioms of A. We note that
$\bigwedge A$
for the sentence that is the conjunction of the axioms of A. We note that
![]() $A+X$
is deductively equivalent to
$A+X$
is deductively equivalent to
![]() $\mathsf {R}_0[\tau _0;\bigwedge A,\varPhi; \top ,X]$
.
$\mathsf {R}_0[\tau _0;\bigwedge A,\varPhi; \top ,X]$
.
A theory is restricted, iff it can be axiomatized by axioms of complexity
![]() $\leqslant n$
, for some fixed n. In [Reference Visser24] it has been verified that sequential restricted c.e. theories can be written as
$\leqslant n$
, for some fixed n. In [Reference Visser24] it has been verified that sequential restricted c.e. theories can be written as
![]() $A+X$
, where A and X satisfy the conditions of Theorem 5.10. So, we have:
$A+X$
, where A and X satisfy the conditions of Theorem 5.10. So, we have:
Corollary 5.11. Any restricted sequential c.e. theory is
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced.
$\mathsf {R}_{0\mathsf {p}}$
-sourced.
Examples of restricted sequential c.e. theories are:
-
•
 $\mho _{\mathsf {PA}} :=\mathsf {S}^1_2+ \mathsf {Con}_1(\mathsf {PA}) + \mathsf {Con}_2(\mathsf {PA}) + \dots $
, where the
$\mho _{\mathsf {PA}} :=\mathsf {S}^1_2+ \mathsf {Con}_1(\mathsf {PA}) + \mathsf {Con}_2(\mathsf {PA}) + \dots $
, where the
 $\mathsf {Con}_i(\mathsf {PA})$
are consistency statements where we restrict the
$\mathsf {Con}_i(\mathsf {PA})$
are consistency statements where we restrict the
 $\mathsf {PA}$
-axioms to those with Gödel number
$\mathsf {PA}$
-axioms to those with Gödel number
 $\leqslant i$
and where we restrict the proofs to those in which only formulas of depth of quantifier alternations
$\leqslant i$
and where we restrict the proofs to those in which only formulas of depth of quantifier alternations
 $\leqslant i$
occur.
$\leqslant i$
occur. -
•
 $\mathrm {I}\Delta _0+\varOmega _1+ \varOmega _2+\dots $
,
$\mathrm {I}\Delta _0+\varOmega _1+ \varOmega _2+\dots $
, -
•
 $\mathsf {EA}+\mathsf {Con}(\mathsf {EA})+ \mathsf {Con}(\mathsf {EA}+\mathsf {Con}(\mathsf {EA}))+ \dots $
,
$\mathsf {EA}+\mathsf {Con}(\mathsf {EA})+ \mathsf {Con}(\mathsf {EA}+\mathsf {Con}(\mathsf {EA}))+ \dots $
, -
•
 $\mathsf {PRA}$
(in a suitable version in finite signature).
$\mathsf {PRA}$
(in a suitable version in finite signature).
We end with a closure condition.
Theorem 5.12. Suppose U and V are
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theories in the same signature
$\mathsf {R}_{0\mathsf {p}}$
-sourced theories in the same signature
![]() $\mathcal {L}$
, as witnessed by
$\mathcal {L}$
, as witnessed by
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
. Suppose the restriction of
$\tau '$
. Suppose the restriction of
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
to the arithmetical signature is a shared part
$\tau '$
to the arithmetical signature is a shared part
![]() $\tau _0$
. Then
$\tau _0$
. Then
![]() $U \cup V$
is
$U \cup V$
is
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced.
$\mathsf {R}_{0\mathsf {p}}$
-sourced.
Proof. We take as witnessing translation
![]() $\tau ^\star $
for
$\tau ^\star $
for
![]() $U\cup V$
, the translation
$U\cup V$
, the translation
![]() $\tau _0$
on the arithmetical vocabulary and
$\tau _0$
on the arithmetical vocabulary and
![]() $\mathsf {P}_{\tau ^\star }(\vec {x}) := (\mathsf {P}_\tau (\vec {x}) \wedge \mathsf {P}_{\tau '}(\vec {x}))$
. Alternatively, we note that
$\mathsf {P}_{\tau ^\star }(\vec {x}) := (\mathsf {P}_\tau (\vec {x}) \wedge \mathsf {P}_{\tau '}(\vec {x}))$
. Alternatively, we note that
![]() $U \cup V$
is deductively equivalent to
$U \cup V$
is deductively equivalent to
![]() $\mathsf {R}_0[\tau _0; \mathsf {P}_\tau (\vec {x}),\mathsf {P}_{\tau '}(\vec {x});\omega ,\omega ]$
.
$\mathsf {R}_0[\tau _0; \mathsf {P}_\tau (\vec {x}),\mathsf {P}_{\tau '}(\vec {x});\omega ,\omega ]$
.
6 Witness comparisons and fixed points
In this section, we give the basic definitions and facts for witness comparison. Moreover, we discuss the Gödel fixed point lemma and its interaction with witness comparison.
6.1 Comparing the witnesses
We define witness comparison. Let
![]() $\phi := \exists x\, \phi _0(x)$
and
$\phi := \exists x\, \phi _0(x)$
and
![]() $\psi := \exists y\, \psi _0(y)$
. We define:
$\psi := \exists y\, \psi _0(y)$
. We define:
-
•
 $\phi \mathbin {\leqslant } \psi :\leftrightarrow \exists x\, (\phi _0(x) \wedge \forall y < x\, \neg \,\psi _0(y))$
,
$\phi \mathbin {\leqslant } \psi :\leftrightarrow \exists x\, (\phi _0(x) \wedge \forall y < x\, \neg \,\psi _0(y))$
, -
•
 $\phi < \psi :\leftrightarrow \exists x\, (\phi _0(x) \wedge \forall y \mathbin {\leqslant } x\, \neg \,\psi _0(y))$
,
$\phi < \psi :\leftrightarrow \exists x\, (\phi _0(x) \wedge \forall y \mathbin {\leqslant } x\, \neg \,\psi _0(y))$
, -
•
 $(\phi \mathbin {\leqslant } \psi )^\bot := (\psi <\phi )$
,
$(\phi \mathbin {\leqslant } \psi )^\bot := (\psi <\phi )$
, -
•
 $(\phi < \psi )^\bot := (\psi \mathbin {\leqslant } \phi )$
.
$(\phi < \psi )^\bot := (\psi \mathbin {\leqslant } \phi )$
.
We have to do some preliminary work to compensate for the fact that in
![]() $\mathsf {R}_0$
we are lacking the axiom
$\mathsf {R}_0$
we are lacking the axiom
![]() $\mathsf {R}5$
which says, for every numeral n, that
$\mathsf {R}5$
which says, for every numeral n, that
![]() $x \leqslant \underline {n} \vee \underline {n}\leqslant x$
. We say that x is well-behaved or
$x \leqslant \underline {n} \vee \underline {n}\leqslant x$
. We say that x is well-behaved or
![]() $\mathsf {wb}(x)$
iff it satisfies
$\mathsf {wb}(x)$
iff it satisfies
![]() $\mathsf {A}1$
and
$\mathsf {A}1$
and
![]() $\mathsf {A}2$
of the definition of certification, i.o.w.,
$\mathsf {A}2$
of the definition of certification, i.o.w.,
![]() $\mathsf {wb}(x)$
iff
$\mathsf {wb}(x)$
iff
![]() $0 \leqslant x$
and
$0 \leqslant x$
and
![]() $\forall y \mathbin {<} x\; \mathsf {s}\hspace{0.02cm} y \leqslant x$
. We say that a sentence is well-behaved if it is of the form
$\forall y \mathbin {<} x\; \mathsf {s}\hspace{0.02cm} y \leqslant x$
. We say that a sentence is well-behaved if it is of the form
![]() $\exists x\, (\mathsf {wb}(x) \wedge \psi (x))$
.
$\exists x\, (\mathsf {wb}(x) \wedge \psi (x))$
.
Remark 6.1. The idea of well-behavedness, though not the name, is due to Cobham, see Jones and Shepherdson [Reference Jones and Shepherdson6]. In fact, for our purposes, we could also have worked with certified instead of well-behaved, but we found it attractive to use the lightest possible means to obtain the results.
We have the following lemma.
Lemma 6.2.
-
a.
 $\mathsf {R}_0 \vdash \mathsf {wb}(x) \to (x< \underline {n} \vee \underline {n} \leqslant x)$
.
$\mathsf {R}_0 \vdash \mathsf {wb}(x) \to (x< \underline {n} \vee \underline {n} \leqslant x)$
. -
b.
 $\mathsf {R}_0 \vdash \mathsf {wb}(x) \to (x\leqslant \underline {n} \vee \underline {n} < x)$
.
$\mathsf {R}_0 \vdash \mathsf {wb}(x) \to (x\leqslant \underline {n} \vee \underline {n} < x)$
.
Proof. (a) can be proved by a simple induction on n and (b) is immediate from (a).
It follows that:
Lemma 6.3. Suppose
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
are 1-
$\sigma '$
are 1-
![]() $\Sigma _1$
-sentences and
$\Sigma _1$
-sentences and
![]() $\sigma '$
is well-behaved.
$\sigma '$
is well-behaved.
-
a. If
 $\mathbb {N} \models \sigma \mathbin {\leqslant } \sigma '$
, then
$\mathbb {N} \models \sigma \mathbin {\leqslant } \sigma '$
, then
 $\mathsf {R}_0 \vdash \neg \, \sigma '\mathbin {<}\sigma $
.
$\mathsf {R}_0 \vdash \neg \, \sigma '\mathbin {<}\sigma $
. -
b. If
 $\mathbb {N} \models \sigma \mathbin {<} \sigma '$
, then,
$\mathbb {N} \models \sigma \mathbin {<} \sigma '$
, then,
 $\mathsf {R}_0 \vdash \neg \, \sigma '\mathbin {\leqslant }\sigma $
.
$\mathsf {R}_0 \vdash \neg \, \sigma '\mathbin {\leqslant }\sigma $
.
Proof. Let
![]() $\sigma = \exists x\,\sigma _0(x)$
and
$\sigma = \exists x\,\sigma _0(x)$
and
![]() $\sigma ' = \exists y\,(\mathsf {wb}(y) \wedge \sigma _0'(y))$
.
$\sigma ' = \exists y\,(\mathsf {wb}(y) \wedge \sigma _0'(y))$
.
We treat (a). Suppose
![]() $\sigma \mathbin {\leqslant } \sigma '$
is true in the natural numbers. Then, for some n, we have
$\sigma \mathbin {\leqslant } \sigma '$
is true in the natural numbers. Then, for some n, we have
![]() $\mathsf {R}_0 \vdash \sigma _0(\underline {n})$
. Moreover, for all
$\mathsf {R}_0 \vdash \sigma _0(\underline {n})$
. Moreover, for all
![]() $k< n$
, we have (†)
$k< n$
, we have (†)
![]() $\mathsf {R}_0\vdash \neg \,\sigma _0'(\underline {k})$
. We reason in
$\mathsf {R}_0\vdash \neg \,\sigma _0'(\underline {k})$
. We reason in
![]() $\mathsf {R}_0$
. Suppose
$\mathsf {R}_0$
. Suppose
![]() $ \sigma '\mathbin {<}\sigma $
. Then, for some well-behaved y, we have
$ \sigma '\mathbin {<}\sigma $
. Then, for some well-behaved y, we have
![]() $\sigma _0'(y)$
and (‡)
$\sigma _0'(y)$
and (‡)
![]() $\forall z\mathbin {\leqslant } y\, \neg \, \sigma _0(z)$
. By Lemma 6.2, we find that
$\forall z\mathbin {\leqslant } y\, \neg \, \sigma _0(z)$
. By Lemma 6.2, we find that
![]() $y < \underline {n}$
or
$y < \underline {n}$
or
![]() $\underline {n} \leqslant y$
. The first disjunct contradicts (†) and the second disjunct contradicts (‡).
$\underline {n} \leqslant y$
. The first disjunct contradicts (†) and the second disjunct contradicts (‡).
The proof of (b) is similar.
We prove the result that gives us the desired applications.
Theorem 6.4. Suppose
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
are 1-
$\sigma '$
are 1-
![]() $\Sigma _1$
-sentences,
$\Sigma _1$
-sentences,
![]() $\sigma '$
is well-behaved and
$\sigma '$
is well-behaved and
![]() $\rho $
is a
$\rho $
is a
![]() $\Sigma _1$
-sentence.
$\Sigma _1$
-sentence.
-
a. If
 $\mathbb {N} \models \sigma \mathbin {\leqslant } \sigma '$
and
$\mathbb {N} \models \sigma \mathbin {\leqslant } \sigma '$
and
 $\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '<\sigma $
, then
$\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '<\sigma $
, then
 $[\rho ]$
is inconsistent.
$[\rho ]$
is inconsistent. -
b. If
 $\mathbb {N} \models \sigma < \sigma '$
and
$\mathbb {N} \models \sigma < \sigma '$
and
 $\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '\mathbin {\leqslant } \sigma $
, then
$\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '\mathbin {\leqslant } \sigma $
, then
 $[\rho ]$
is inconsistent.
$[\rho ]$
is inconsistent.
Proof. We prove (a). Suppose
![]() $\mathbb {N} \models \sigma \mathbin {\leqslant } \sigma '$
and
$\mathbb {N} \models \sigma \mathbin {\leqslant } \sigma '$
and
![]() $\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '\mathbin {<}\sigma $
. By Lemma 6.3, we have
$\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '\mathbin {<}\sigma $
. By Lemma 6.3, we have
![]() $\mathsf {R}_0 \vdash \neg \, \sigma '\mathbin {<} \sigma $
, and hence
$\mathsf {R}_0 \vdash \neg \, \sigma '\mathbin {<} \sigma $
, and hence
![]() $\mathsf {R}_0 \vdash \neg \, \rho $
. It follows that
$\mathsf {R}_0 \vdash \neg \, \rho $
. It follows that
![]() $\mathbb {N} \models \neg \, \rho $
. So, by Theorem 2.9, that
$\mathbb {N} \models \neg \, \rho $
. So, by Theorem 2.9, that
![]() $[\rho ] \vdash \mathsf {R}_0$
, and, hence,
$[\rho ] \vdash \mathsf {R}_0$
, and, hence,
![]() $[\rho ] \vdash \neg \, \rho $
. On the other hand, again by Theorem 2.9, we have
$[\rho ] \vdash \neg \, \rho $
. On the other hand, again by Theorem 2.9, we have
![]() $[\rho ] \vdash \rho $
. Ergo,
$[\rho ] \vdash \rho $
. Ergo,
![]() $[\rho ]$
is inconsistent.
$[\rho ]$
is inconsistent.
By a trivial adaptation of the above argument, we also have:
Theorem 6.5. Let
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
be 1-
$\sigma '$
be 1-
![]() $\Sigma _1$
-sentences, where
$\Sigma _1$
-sentences, where
![]() $\sigma '$
is well behaved. Let
$\sigma '$
is well behaved. Let
![]() $\rho $
be any
$\rho $
be any
![]() $\Sigma _1$
-sentence. We have:
$\Sigma _1$
-sentence. We have:
-
a. If
 $\mathbb {N} \models \sigma \mathbin {\leqslant } \sigma '$
and
$\mathbb {N} \models \sigma \mathbin {\leqslant } \sigma '$
and
 $\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '\mathbin {<} \sigma $
, then
$\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '\mathbin {<} \sigma $
, then  is inconsistent.
is inconsistent. -
b. If
 $\mathbb {N} \models \sigma \mathbin {<} \sigma '$
and
$\mathbb {N} \models \sigma \mathbin {<} \sigma '$
and
 $\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '\mathbin {\leqslant } \sigma $
, then
$\mathsf {R}_0 \vdash \rho \leftrightarrow \sigma '\mathbin {\leqslant } \sigma $
, then  is inconsistent.
is inconsistent.
6.2 The fixed point lemma
In
![]() $\mathsf {R}_0$
we can prove the representability of all recursive functions as the following lemma describes.
$\mathsf {R}_0$
we can prove the representability of all recursive functions as the following lemma describes.
Lemma 6.6. For every recursive function F there is a 1-
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\sigma (x,y)$
such that, whenever
$\sigma (x,y)$
such that, whenever
![]() $F(n)=m$
, we have
$F(n)=m$
, we have
![]() $\mathsf {R}_0 \vdash \forall y\, (\sigma (\underline {n},y) \leftrightarrow \underline {m}=y)$
.
$\mathsf {R}_0 \vdash \forall y\, (\sigma (\underline {n},y) \leftrightarrow \underline {m}=y)$
.
Proof. Consider any recursive function F and let
![]() $\sigma ^\star (x,y) = \exists z\, \sigma ^\star _0(x,y,z)$
be any 1-
$\sigma ^\star (x,y) = \exists z\, \sigma ^\star _0(x,y,z)$
be any 1-
![]() $\Sigma _1$
-formula representing the graph of F. We take
$\Sigma _1$
-formula representing the graph of F. We take
 $$ \begin{align*} \sigma(x,y) :\leftrightarrow \exists z\, \big(\mathsf{wb}(z) \wedge y \leqslant z \wedge \exists u \leqslant z\, &\sigma^\star_0(x,y,u) \, \wedge \\ &\forall a \leqslant z\, \forall b \leqslant z\, (\sigma^\star_0(x,a,b) \to a = y)\big). \end{align*} $$
$$ \begin{align*} \sigma(x,y) :\leftrightarrow \exists z\, \big(\mathsf{wb}(z) \wedge y \leqslant z \wedge \exists u \leqslant z\, &\sigma^\star_0(x,y,u) \, \wedge \\ &\forall a \leqslant z\, \forall b \leqslant z\, (\sigma^\star_0(x,a,b) \to a = y)\big). \end{align*} $$
We now use Lemma 6.2, to mimic the well-known proof of the analog of the Lemma for the case of
![]() $\mathsf {R}$
.
$\mathsf {R}$
.
We can prove the usual fixed point lemma using a representation of the substitution function provided by Lemma 6.6. However, we need a bit more.
Theorem 6.7.
-
i. Suppose
 $\sigma (x)$
is
$\sigma (x)$
is
 $\Sigma _1$
. Then, we can find a
$\Sigma _1$
. Then, we can find a
 $\Sigma _1$
-formula
$\Sigma _1$
-formula
 $\eta $
such that
$\eta $
such that
 $\mathsf {R}_0 \vdash \eta \leftrightarrow \sigma (\ulcorner {\eta }\urcorner )$
.
$\mathsf {R}_0 \vdash \eta \leftrightarrow \sigma (\ulcorner {\eta }\urcorner )$
. -
ii. Suppose
 $\sigma (x,y)$
and
$\sigma (x,y)$
and
 $\sigma '(x,y)$
are
$\sigma '(x,y)$
are
 $\Sigma _1$
-formulas. We can find
$\Sigma _1$
-formulas. We can find
 $\Sigma _1$
-formulas
$\Sigma _1$
-formulas
 $\eta $
and
$\eta $
and
 $\eta '$
such that
$\eta '$
such that
 $\mathsf {R}_0 \vdash \eta \leftrightarrow \sigma (\ulcorner {\eta }\urcorner ,\ulcorner {\eta '}\urcorner )$
and
$\mathsf {R}_0 \vdash \eta \leftrightarrow \sigma (\ulcorner {\eta }\urcorner ,\ulcorner {\eta '}\urcorner )$
and
 $\mathsf {R}_0 \vdash \eta ' \leftrightarrow \sigma '(\ulcorner {\eta }\urcorner ,\ulcorner {\eta '}\urcorner )$
.
$\mathsf {R}_0 \vdash \eta ' \leftrightarrow \sigma '(\ulcorner {\eta }\urcorner ,\ulcorner {\eta '}\urcorner )$
.
Proof. We treat (i).
We can obtain the desired result by a careful modification of the usual proof of the fixed point lemma. Alternatively, we can proceed as follows. Let
![]() $\Sigma _1^\dagger $
be the class given by
$\Sigma _1^\dagger $
be the class given by
![]() $\chi ::= \sigma \mid (\chi \wedge \chi ) \mid \exists v\,\chi $
. Here
$\chi ::= \sigma \mid (\chi \wedge \chi ) \mid \exists v\,\chi $
. Here
![]() $\sigma $
ranges over
$\sigma $
ranges over
![]() $\Sigma _1$
-sentences. We can easily rewrite a
$\Sigma _1$
-sentences. We can easily rewrite a
![]() $\Sigma _1^\dagger $
-sentence to a
$\Sigma _1^\dagger $
-sentence to a
![]() $\Sigma _1$
-sentence by moving the relevant existential quantifiers out. The usual fixed point calculation delivers a
$\Sigma _1$
-sentence by moving the relevant existential quantifiers out. The usual fixed point calculation delivers a
![]() $\Sigma ^\dagger _1$
-sentence using the wide scope elimination for the substitution function. Suppose we arithmetize this normalization function say as
$\Sigma ^\dagger _1$
-sentence using the wide scope elimination for the substitution function. Suppose we arithmetize this normalization function say as
![]() $\mathsf {norm}$
. We can represent this function in
$\mathsf {norm}$
. We can represent this function in
![]() $\mathsf {R}_0$
by Lemma 6.6. We can construct a
$\mathsf {R}_0$
by Lemma 6.6. We can construct a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\sigma '(x)$
that functions as
$\sigma '(x)$
that functions as
![]() $\sigma (\mathsf {norm}(x))$
. Let
$\sigma (\mathsf {norm}(x))$
. Let
![]() $\eta '$
be the ordinary Gödel fixed point of
$\eta '$
be the ordinary Gödel fixed point of
![]() $\sigma '$
and let
$\sigma '$
and let
![]() $\eta $
be the normalized form of
$\eta $
be the normalized form of
![]() $\eta '$
. Then, we have:
$\eta '$
. Then, we have:
 $$ \begin{align*} \mathsf{R}_0 \vdash \eta & \leftrightarrow \eta' \\ & \leftrightarrow \sigma'(\ulcorner{\eta'}\urcorner) \\ & \leftrightarrow \sigma(\ulcorner{\eta}\urcorner). \end{align*} $$
$$ \begin{align*} \mathsf{R}_0 \vdash \eta & \leftrightarrow \eta' \\ & \leftrightarrow \sigma'(\ulcorner{\eta'}\urcorner) \\ & \leftrightarrow \sigma(\ulcorner{\eta}\urcorner). \end{align*} $$
The alternative proof is easily adapted to deliver also the desired double fixed point promised in (ii).
We note that the trick of the alternative proof will work for all kinds of normalizations.
A disadvantage of the modified Gödel-style fixed point construction is that it does not preserve witness comparison form. For the results in the next sections, this is not really needed, but it may sometimes lead to less elegant formulations. How nice it would be if we could preserve almost all forms of the original formula. An elegant way to do this is to employ a self-referential Gödel-numbering, which has self-reference built in.
The idea of a self-referential Gödel numbering was introduced by Saul Kripke in [Reference Kripke7, Footnote 6]. It was worked out in some detail in [Reference Visser, Gabbay and Guenthner19]. Recently, two papers appeared exploring the notion further, to wit [Reference Kripke8] and [Reference Grabmayr and Visser4]. As far as we know the only place where the idea is truly applied is [Reference Grabmayr3].
We follow the realization of [Reference Visser, Gabbay and Guenthner19]. The idea is simple. We extend
![]() $\mathbb {L}_{\mathsf {a}}$
with a fresh constant
$\mathbb {L}_{\mathsf {a}}$
with a fresh constant
![]() $\mathsf {c}$
and employ a standard Gödel numbering for the extended language. We then take the standard Gödel number
$\mathsf {c}$
and employ a standard Gödel numbering for the extended language. We then take the standard Gödel number
![]() $\ulcorner {\phi (\mathsf {c})}\urcorner $
for the extended language to be the self-referential Gödel number of
$\ulcorner {\phi (\mathsf {c})}\urcorner $
for the extended language to be the self-referential Gödel number of
![]() $\phi (\ulcorner {\phi (\mathsf {c})}\urcorner )$
for
$\phi (\ulcorner {\phi (\mathsf {c})}\urcorner )$
for
![]() $\mathbb {L}_{\mathsf {a}}$
. Without further measures, the resulting Gödel numbering is not functional from sentences to numbers. The functionality of a Gödel number is not strictly needed, but we opt for making the numbering functional by stipulating that we take the smallest number assigned to a sentence by our non-functional version. In [Reference Visser, Gabbay and Guenthner19] it is carefully verified that, for a decent choice of the input standard Gödel numbering, the numbering so obtained fulfills all the desiderata of a self-referential Gödel numbering. We write
$\mathbb {L}_{\mathsf {a}}$
. Without further measures, the resulting Gödel numbering is not functional from sentences to numbers. The functionality of a Gödel number is not strictly needed, but we opt for making the numbering functional by stipulating that we take the smallest number assigned to a sentence by our non-functional version. In [Reference Visser, Gabbay and Guenthner19] it is carefully verified that, for a decent choice of the input standard Gödel numbering, the numbering so obtained fulfills all the desiderata of a self-referential Gödel numbering. We write
![]() $\lceil {\phi }\rceil $
for the self-referential Gödel number of
$\lceil {\phi }\rceil $
for the self-referential Gödel number of
![]() $\phi $
. The crucial property is that for any
$\phi $
. The crucial property is that for any
![]() $\phi (x)$
with at most x free, we can effectively find a
$\phi (x)$
with at most x free, we can effectively find a
![]() $\psi $
with
$\psi $
with
![]() $\psi = \phi (\lceil {\psi }\rceil )$
.
$\psi = \phi (\lceil {\psi }\rceil )$
.
In this paper we mostly opt for the ordinary numbering, accepting the use of Theorem 6.7 as the way to go. We will prove Theorem 8.17 twice, once with an ordinary numbering and once with a self-referential one in order to illustrate the use of a self-referential numbering.
7 Vaught’s theorems revisited
We give two proofs of Theorem 2.5 and prove a generalization of Theorem 2.6.
Theorem 2.5 (Vaught [Reference Vaught17, 5.2])
The theory
![]() $\mathsf {R}_0$
is strongly effectively inseparable.
$\mathsf {R}_0$
is strongly effectively inseparable.
First Proof
Let
![]() $i, j \in \omega $
be such that
$i, j \in \omega $
be such that
![]() $\mathsf {R}_{0\mathfrak {p}} \subseteq \mathsf {W}_{i}$
,
$\mathsf {R}_{0\mathfrak {p}} \subseteq \mathsf {W}_{i}$
,
![]() $\emptyset _{\mathfrak {r}} \subseteq \mathsf {W}_{j}$
, and
$\emptyset _{\mathfrak {r}} \subseteq \mathsf {W}_{j}$
, and
![]() $\mathsf {W}_{i} \cap \mathsf {W}_{j} = \emptyset $
. Let
$\mathsf {W}_{i} \cap \mathsf {W}_{j} = \emptyset $
. Let
![]() $(X, Y)$
be any effectively inseparable pair of c.e. sets. We can clearly find 1-
$(X, Y)$
be any effectively inseparable pair of c.e. sets. We can clearly find 1-
![]() $\Sigma _1$
-formulas
$\Sigma _1$
-formulas
![]() $\xi (x)$
and
$\xi (x)$
and
![]() $\eta (x)$
that represent X respectively Y. We can clearly arrange that
$\eta (x)$
that represent X respectively Y. We can clearly arrange that
![]() $\xi $
and
$\xi $
and
![]() $\eta $
are well-behaved.
$\eta $
are well-behaved.
For each natural number n, let
![]() $\sigma _n$
be the 1-
$\sigma _n$
be the 1-
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\xi (\underline {n}) \mathbin {\leqslant } \eta (\underline {n})$
. We can effectively find natural numbers
$\xi (\underline {n}) \mathbin {\leqslant } \eta (\underline {n})$
. We can effectively find natural numbers
![]() $i'$
and
$i'$
and
![]() $j'$
such that
$j'$
such that
![]() $\mathsf {W}_{i'} = \{n \in \omega \mid [\sigma _n] \in \mathsf {W}_{i}\}$
and
$\mathsf {W}_{i'} = \{n \in \omega \mid [\sigma _n] \in \mathsf {W}_{i}\}$
and
![]() $\mathsf {W}_{j'} = \{n \in \omega \mid [\sigma _n]\in \mathsf {W}_{j}\}$
.Footnote
4
Obviously,
$\mathsf {W}_{j'} = \{n \in \omega \mid [\sigma _n]\in \mathsf {W}_{j}\}$
.Footnote
4
Obviously,
![]() $\mathsf {W}_{i'} \cap \mathsf {W}_{j'} = \emptyset $
.
$\mathsf {W}_{i'} \cap \mathsf {W}_{j'} = \emptyset $
.
Suppose
![]() $n \in X$
. Since X and Y are disjoint, we find
$n \in X$
. Since X and Y are disjoint, we find
![]() $\mathbb {N} \models \sigma _n$
. By Theorem 2.9, we have
$\mathbb {N} \models \sigma _n$
. By Theorem 2.9, we have
![]() $\mathsf {R}_0 \vdash [\sigma _n]$
, that is,
$\mathsf {R}_0 \vdash [\sigma _n]$
, that is,
![]() $[\sigma _n] \in \mathsf {R}_{0\mathfrak {p}}$
. Then,
$[\sigma _n] \in \mathsf {R}_{0\mathfrak {p}}$
. Then,
![]() $[\sigma _n] \in \mathsf {W}_{i}$
, and hence
$[\sigma _n] \in \mathsf {W}_{i}$
, and hence
![]() $n \in \mathsf {W}_{i'}$
.
$n \in \mathsf {W}_{i'}$
.
Suppose
![]() $n \in Y$
. We find
$n \in Y$
. We find
![]() $\mathbb {N} \models \sigma _n^\bot $
. By Theorem 6.4, we obtain
$\mathbb {N} \models \sigma _n^\bot $
. By Theorem 6.4, we obtain
![]() $ [\sigma _n] \vdash \bot $
, that is
$ [\sigma _n] \vdash \bot $
, that is
![]() $[\sigma _n] \in \emptyset _{\mathfrak {r}}$
. Hence,
$[\sigma _n] \in \emptyset _{\mathfrak {r}}$
. Hence,
![]() $[\sigma _n] \in \mathsf {W}_{j}$
, and, so,
$[\sigma _n] \in \mathsf {W}_{j}$
, and, so,
![]() $n \in \mathsf {W}_{j'}$
.
$n \in \mathsf {W}_{j'}$
.
We have shown that
![]() $\mathsf {W}_{i'}$
and
$\mathsf {W}_{i'}$
and
![]() $\mathsf {W}_{j'}$
separate
$\mathsf {W}_{j'}$
separate
![]() $(X, Y)$
. By the effective inseparability of
$(X, Y)$
. By the effective inseparability of
![]() $(X, Y)$
, we can effectively find a number
$(X, Y)$
, we can effectively find a number
![]() $m^\star $
such that
$m^\star $
such that
![]() $m^\star \notin \mathsf {W}_{i'} \cup \mathsf {W}_{j'}$
. Then,
$m^\star \notin \mathsf {W}_{i'} \cup \mathsf {W}_{j'}$
. Then,
![]() $[\sigma _{m^\star }] \notin \mathsf {W}_{i} \cup \mathsf {W}_{j}$
. Thus, we have shown that
$[\sigma _{m^\star }] \notin \mathsf {W}_{i} \cup \mathsf {W}_{j}$
. Thus, we have shown that
![]() $(\mathsf {R}_{0\mathfrak {p}}, \emptyset _{\mathfrak {r}})$
is effectively inseparable.
$(\mathsf {R}_{0\mathfrak {p}}, \emptyset _{\mathfrak {r}})$
is effectively inseparable.
Second Proof
Let X and Y be any c.e. sets separating
![]() $\mathsf {R}_{0{\mathfrak {p}}}$
and
$\mathsf {R}_{0{\mathfrak {p}}}$
and
![]() $\emptyset _{{\mathfrak {r}}}$
. We assume that
$\emptyset _{{\mathfrak {r}}}$
. We assume that
![]() $x \in X$
and
$x \in X$
and
![]() $x\in Y$
are represented by well-behaved 1-
$x\in Y$
are represented by well-behaved 1-
![]() $\Sigma _1$
-formulas
$\Sigma _1$
-formulas
![]() $\xi $
and
$\xi $
and
![]() $\eta $
. By Theorem 6.7, we can effectively find a
$\eta $
. By Theorem 6.7, we can effectively find a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\rho $
satisfying the following equivalence:
$\rho $
satisfying the following equivalence:
![]() $ \mathsf {R}_0 \vdash \rho \leftrightarrow \eta ({[ \rho ]}) \mathbin {\leqslant } \xi ({[ \rho ]}) $
.
$ \mathsf {R}_0 \vdash \rho \leftrightarrow \eta ({[ \rho ]}) \mathbin {\leqslant } \xi ({[ \rho ]}) $
.
Suppose
![]() ${[ \rho ]} \in X$
. Since X and Y are disjoint, we have
${[ \rho ]} \in X$
. Since X and Y are disjoint, we have
![]() ${[ \rho ]} \notin Y$
. It follows that
${[ \rho ]} \notin Y$
. It follows that
![]() $\mathbb N \models \xi ({[ \rho ]}) \mathbin {<} \eta ({[ \rho ]})$
and, thus, by Theorem 6.4, that
$\mathbb N \models \xi ({[ \rho ]}) \mathbin {<} \eta ({[ \rho ]})$
and, thus, by Theorem 6.4, that
![]() ${[ \rho ]}$
is inconsistent, i.e.,
${[ \rho ]}$
is inconsistent, i.e.,
![]() ${[ \rho ]} \in \emptyset _{\mathfrak {r}}$
. We may conclude that
${[ \rho ]} \in \emptyset _{\mathfrak {r}}$
. We may conclude that
![]() $X \cap \emptyset _{\mathfrak {r}}$
is non-empty. But this is a contradiction.
$X \cap \emptyset _{\mathfrak {r}}$
is non-empty. But this is a contradiction.
Suppose
![]() ${[ \rho ]} \in Y$
. Since X and Y are disjoint, we have
${[ \rho ]} \in Y$
. Since X and Y are disjoint, we have
![]() $\mathbb {N} \models \rho $
. By Theorem 2.9, we find
$\mathbb {N} \models \rho $
. By Theorem 2.9, we find
![]() $\mathsf {R}_0 \vdash {[ \rho ]}$
, i.e.,
$\mathsf {R}_0 \vdash {[ \rho ]}$
, i.e.,
![]() ${[ \rho ]} \in \mathsf {R}_{0\mathfrak {p}}$
. Thus,
${[ \rho ]} \in \mathsf {R}_{0\mathfrak {p}}$
. Thus,
![]() $Y \cap \mathsf {R}_{0\mathfrak {p}}$
is non-empty. This is a contradiction.
$Y \cap \mathsf {R}_{0\mathfrak {p}}$
is non-empty. This is a contradiction.
Therefore,
![]() ${[ \rho ]} \notin X \cup Y$
. Since we can find
${[ \rho ]} \notin X \cup Y$
. Since we can find
![]() ${[ \rho ]}$
effectively, we have shown that
${[ \rho ]}$
effectively, we have shown that
![]() $(\mathsf {R}_{0\mathfrak {p}}, \emptyset _{\mathfrak {r}})$
is effectively inseparable.
$(\mathsf {R}_{0\mathfrak {p}}, \emptyset _{\mathfrak {r}})$
is effectively inseparable.
Let
![]() $\mathcal {F}$
be the set of all
$\mathcal {F}$
be the set of all
![]() $\mathbb {L}_{\mathsf {a}}$
-sentences having a finite model. Since
$\mathbb {L}_{\mathsf {a}}$
-sentences having a finite model. Since
![]() $\mathsf {R}_{0\mathfrak {p}} \subseteq \mathcal {F}$
and
$\mathsf {R}_{0\mathfrak {p}} \subseteq \mathcal {F}$
and
![]() $\mathcal {F} \cap \emptyset _{\mathfrak {r}} = \emptyset $
, we obtain the following version of Trakhtenbrot’s theorem as a corollary.
$\mathcal {F} \cap \emptyset _{\mathfrak {r}} = \emptyset $
, we obtain the following version of Trakhtenbrot’s theorem as a corollary.
Corollary 7.1 (Trakhtenbrot [Reference Trachtenbrot16])
The pair
![]() $(\mathcal {F}, \emptyset _{\mathfrak {r}})$
is effectively inseparable.
$(\mathcal {F}, \emptyset _{\mathfrak {r}})$
is effectively inseparable.
We note that our version of Trakhtenbrot’s Theorem is formulated for the signature
![]() $\mathbb {L}_{\mathsf {a}}$
. We can generalize it to other signatures (with at least one relation symbol with arity
$\mathbb {L}_{\mathsf {a}}$
. We can generalize it to other signatures (with at least one relation symbol with arity
![]() $\geq 2$
) by the usual tricks of translating a finite signature into the signature with one binary relation symbol; see e.g., [Reference Hodges5, Chapter 5.5]. Alternatively, we can replace the use of theories-of-a-number by the use of very weak set theories as developed, e.g., in [Reference Pakhomov11].
$\geq 2$
) by the usual tricks of translating a finite signature into the signature with one binary relation symbol; see e.g., [Reference Hodges5, Chapter 5.5]. Alternatively, we can replace the use of theories-of-a-number by the use of very weak set theories as developed, e.g., in [Reference Pakhomov11].
We then turn to Theorem 2.6. Before generalizing Theorem 2.6, we introduce the following notions.
Definition 7.2. Let T be an
![]() $\mathcal {L}$
-theory and
$\mathcal {L}$
-theory and
![]() $\mathcal {X}$
be a set of
$\mathcal {X}$
be a set of
![]() $\mathcal {L}$
-sentences.
$\mathcal {L}$
-sentences.
-
1. We say that T is effectively half-essentially
 $\mathcal {X}$
-incomplete iff there exists a partial computable function
$\mathcal {X}$
-incomplete iff there exists a partial computable function
 $\varPhi $
such that for any natural number i, if
$\varPhi $
such that for any natural number i, if
 $\mathsf {W}_{i}$
is a c.e.
$\mathsf {W}_{i}$
is a c.e.
 $\mathcal {L}$
-theory such that
$\mathcal {L}$
-theory such that
 $T + \mathsf {W}_{i}$
is consistent, then
$T + \mathsf {W}_{i}$
is consistent, then
 $\varPhi (i)$
converges,
$\varPhi (i)$
converges,
 $\varPhi (i) \in \mathcal {X}$
,
$\varPhi (i) \in \mathcal {X}$
,
 $T \nvdash \varPhi (i)$
and
$T \nvdash \varPhi (i)$
and
 $\mathsf {W}_{i} \nvdash \neg \, \varPhi (i)$
.
$\mathsf {W}_{i} \nvdash \neg \, \varPhi (i)$
. -
2. We say that T is
 $\mathcal {X}$
-creative iff there exists a partial computable function
$\mathcal {X}$
-creative iff there exists a partial computable function
 $\varPsi $
such that for any natural number i, if
$\varPsi $
such that for any natural number i, if
 $T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
, then
$T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
, then
 $\varPsi (i)$
converges,
$\varPsi (i)$
converges,
 $\varPsi (i) \in \mathcal {X}$
, and
$\varPsi (i) \in \mathcal {X}$
, and
 $\varPsi (i) \notin T_{\mathfrak {p}} \cup \mathsf {W}_{i}$
.
$\varPsi (i) \notin T_{\mathfrak {p}} \cup \mathsf {W}_{i}$
.
Actually, we prove that these two notions are equivalent.
Proposition 7.3. For any
![]() $\mathcal {L}$
-theory T and any set
$\mathcal {L}$
-theory T and any set
![]() $\mathcal {X}$
of
$\mathcal {X}$
of
![]() $\mathcal {L}$
-sentences, the following are equivalent:
$\mathcal {L}$
-sentences, the following are equivalent:
-
a. T is effectively half-essentially
 $\mathcal {X}$
-incomplete.
$\mathcal {X}$
-incomplete. -
b. T is
 $\mathcal {X}$
-creative.
$\mathcal {X}$
-creative.
Proof. “(a) to (b)”. Let
![]() $\varPhi $
be a partial computable function witnessing the effective half-essential
$\varPhi $
be a partial computable function witnessing the effective half-essential
![]() $\mathcal {X}$
-incompleteness of T. Let
$\mathcal {X}$
-incompleteness of T. Let
![]() $\mathsf {W}_{i}$
be any c.e. set such that
$\mathsf {W}_{i}$
be any c.e. set such that
![]() $T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
. By using the recursion theorem, we can effectively find a natural number k from i such that
$T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
. By using the recursion theorem, we can effectively find a natural number k from i such that
 $$\begin{align*}\mathsf{W}_{k} = \begin{cases} \{\neg\, \varPhi(k)\} & \text{if}\ \varPhi(k) {\downarrow}\ \text{and}\ \varPhi(k) \in \mathsf{W}_{i}, \\ \emptyset & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\mathsf{W}_{k} = \begin{cases} \{\neg\, \varPhi(k)\} & \text{if}\ \varPhi(k) {\downarrow}\ \text{and}\ \varPhi(k) \in \mathsf{W}_{i}, \\ \emptyset & \text{otherwise.} \end{cases} \end{align*}$$
If
![]() $T + \mathsf {W}_{k}$
were inconsistent, then there would be a sentence
$T + \mathsf {W}_{k}$
were inconsistent, then there would be a sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $T \vdash \varphi $
and
$T \vdash \varphi $
and
![]() $\mathsf {W}_{k} \vdash \neg \, \varphi $
. Since T is consistent, we would have
$\mathsf {W}_{k} \vdash \neg \, \varphi $
. Since T is consistent, we would have
![]() $\varPhi (k) {\downarrow } \in \mathsf {W}_{i}$
and
$\varPhi (k) {\downarrow } \in \mathsf {W}_{i}$
and
![]() $\mathsf {W}_{k} = \{\neg \, \varPhi (k)\}$
. In this case, we would obtain
$\mathsf {W}_{k} = \{\neg \, \varPhi (k)\}$
. In this case, we would obtain
![]() $T \vdash \varPhi (k)$
. Hence
$T \vdash \varPhi (k)$
. Hence
![]() $\varPhi (k) \in T_{\mathfrak {p}} \cap \mathsf {W}_{i}$
, a contradiction.
$\varPhi (k) \in T_{\mathfrak {p}} \cap \mathsf {W}_{i}$
, a contradiction.
Thus,
![]() $T + \mathsf {W}_{k}$
is consistent. By the effective half-essential
$T + \mathsf {W}_{k}$
is consistent. By the effective half-essential
![]() $\mathcal {X}$
-incompleteness of T, we have
$\mathcal {X}$
-incompleteness of T, we have
![]() $\varPhi (k){\downarrow } \in \mathcal {X}$
,
$\varPhi (k){\downarrow } \in \mathcal {X}$
,
![]() $T \nvdash \varPhi (k)$
, and
$T \nvdash \varPhi (k)$
, and
![]() $\mathsf {W}_{k} \nvdash \neg \, \varPhi (k)$
. In particular,
$\mathsf {W}_{k} \nvdash \neg \, \varPhi (k)$
. In particular,
![]() $\mathsf {W}_{k} \nvdash \neg \, \varPhi (k)$
implies
$\mathsf {W}_{k} \nvdash \neg \, \varPhi (k)$
implies
![]() $\varPhi (k) \notin \mathsf {W}_{i}$
. Therefore the partial computable function
$\varPhi (k) \notin \mathsf {W}_{i}$
. Therefore the partial computable function
![]() $\varPsi (i) : = \varPhi (k)$
witnesses the
$\varPsi (i) : = \varPhi (k)$
witnesses the
![]() $\mathcal {X}$
-creativity of T.
$\mathcal {X}$
-creativity of T.
“(b) to (a)”. Let
![]() $\varPsi $
be a partial computable function witnessing the
$\varPsi $
be a partial computable function witnessing the
![]() $\mathcal {X}$
-creativity of T. Let
$\mathcal {X}$
-creativity of T. Let
![]() $\mathsf {W}_{i}$
be any c.e.
$\mathsf {W}_{i}$
be any c.e.
![]() $\mathcal {L}$
-theory such that
$\mathcal {L}$
-theory such that
![]() $T + \mathsf {W}_{i}$
is consistent. We can effectively find a number k from i such that
$T + \mathsf {W}_{i}$
is consistent. We can effectively find a number k from i such that
![]() $\mathsf {W}_{k} = \mathsf {W}_{i \mathfrak {r}}$
. Then,
$\mathsf {W}_{k} = \mathsf {W}_{i \mathfrak {r}}$
. Then,
![]() $T_{\mathfrak {p}} \cap \mathsf {W}_{k} = \emptyset $
. By the
$T_{\mathfrak {p}} \cap \mathsf {W}_{k} = \emptyset $
. By the
![]() $\mathcal {X}$
-creativity of T, we have
$\mathcal {X}$
-creativity of T, we have
![]() $\varPsi (k){\downarrow } \in \mathcal {X}$
and
$\varPsi (k){\downarrow } \in \mathcal {X}$
and
![]() $\varPsi (k) \notin T_{\mathfrak {p}} \cup \mathsf {W}_{i\mathfrak {r}}$
. Therefore, the partial computable function
$\varPsi (k) \notin T_{\mathfrak {p}} \cup \mathsf {W}_{i\mathfrak {r}}$
. Therefore, the partial computable function
![]() $\varPhi (i) : = \varPsi (k)$
witnesses the effective half-essential
$\varPhi (i) : = \varPsi (k)$
witnesses the effective half-essential
![]() $\mathcal {X}$
-incompleteness of T.
$\mathcal {X}$
-incompleteness of T.
We proceed with a generalization of Theorem 2.6. For each
![]() $\mathcal {L}$
-theory T, let
$\mathcal {L}$
-theory T, let
![]() $\mathsf {coTh}_{T} : = \{\varphi \mid \varphi $
is an
$\mathsf {coTh}_{T} : = \{\varphi \mid \varphi $
is an
![]() $\mathcal {L}$
-sentence and
$\mathcal {L}$
-sentence and
![]() $\varphi \vdash T\}$
.
$\varphi \vdash T\}$
.
Theorem 7.4. Every
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory T is
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory T is
![]() $\mathsf {coTh}_{T}$
-creative.
$\mathsf {coTh}_{T}$
-creative.
Proof. Let T be a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e.
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e.
![]() $\mathcal {L}$
-theory and let
$\mathcal {L}$
-theory and let
![]() $\mathsf {W}_{i}$
be any c.e. set such that
$\mathsf {W}_{i}$
be any c.e. set such that
![]() $T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
. Let
$T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
. Let
![]() $\alpha _i$
be a well-behaved 1-
$\alpha _i$
be a well-behaved 1-
![]() $\Sigma _1$
-formula that represents
$\Sigma _1$
-formula that represents
![]() $\mathsf {W}_{i}$
and let
$\mathsf {W}_{i}$
and let
![]() $\mathsf {Pr}_T$
be a well-behaved 1-
$\mathsf {Pr}_T$
be a well-behaved 1-
![]() $\Sigma _1$
-formula that represents provability in T. By Theorem 6.7, we can effectively find a
$\Sigma _1$
-formula that represents provability in T. By Theorem 6.7, we can effectively find a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\jmath $
from i satisfying
$\jmath $
from i satisfying ![]() Footnote
5
Footnote
5
Suppose ![]() . Then, we have
. Then, we have ![]() because
because
![]() $T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
. By Theorem 6.5,
$T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
. By Theorem 6.5, ![]() is inconsistent. Then, we have
is inconsistent. Then, we have ![]() . This is a contradiction.
. This is a contradiction.
Suppose ![]() . Since
. Since
![]() $T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
, we have
$T_{\mathfrak {p}} \cap \mathsf {W}_{i} = \emptyset $
, we have
![]() $\mathbb {N} \models \jmath $
. By Theorem 5.3, we find
$\mathbb {N} \models \jmath $
. By Theorem 5.3, we find ![]() . Thus,
. Thus,
![]() $T_{\mathfrak {p}} \cap \mathsf {W}_{i}$
is non-empty. This is a contradiction.
$T_{\mathfrak {p}} \cap \mathsf {W}_{i}$
is non-empty. This is a contradiction.
Therefore, we obtain ![]() . This implies that
. This implies that
![]() $\jmath $
is false. By Theorem 5.3 again, we obtain that
$\jmath $
is false. By Theorem 5.3 again, we obtain that ![]() , i.e.,
, i.e., ![]() . Then the partial computable function
. Then the partial computable function ![]() witnesses the
witnesses the
![]() $\mathsf {coTh}_{T}$
-creativity of T.
$\mathsf {coTh}_{T}$
-creativity of T.
Corollary 7.5. Every
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory T is effectively half-essentially
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory T is effectively half-essentially
![]() $\mathsf {coTh}_{T}$
-incomplete.
$\mathsf {coTh}_{T}$
-incomplete.
Consider a
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e.
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e.
![]() $\mathcal {L}$
-theory T. If U is a c.e.
$\mathcal {L}$
-theory T. If U is a c.e.
![]() $\mathcal {L}$
-theory such that
$\mathcal {L}$
-theory such that
![]() $T + U$
is consistent, then by Corollary 7.5, we can effectively find a sentence
$T + U$
is consistent, then by Corollary 7.5, we can effectively find a sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $\varphi \vdash T$
,
$\varphi \vdash T$
,
![]() $T \nvdash \varphi $
, and
$T \nvdash \varphi $
, and
![]() $U \nvdash \neg \, \varphi $
. Then the
$U \nvdash \neg \, \varphi $
. Then the
![]() $\mathcal {L}$
-theory A axiomatized by
$\mathcal {L}$
-theory A axiomatized by
![]() $\varphi $
is a proper extension of T such that
$\varphi $
is a proper extension of T such that
![]() $A+U$
is consistent. This shows that Corollary 7.5 is in fact a generalization of Theorem 2.6.
$A+U$
is consistent. This shows that Corollary 7.5 is in fact a generalization of Theorem 2.6.
Corollary 7.6. Every
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory is deductively equivalent to the intersection of the deductive closures of its finite same-signature extensions.
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory is deductively equivalent to the intersection of the deductive closures of its finite same-signature extensions.
We note that not every c.e. theory is deductively equivalent to the intersection of the deductive closures of its finite same-signature extensions. For example,
![]() $\mathsf {PA}$
has no consistent finite same-signature extensions. So, the relevant intersection would be the inconsistent
$\mathsf {PA}$
has no consistent finite same-signature extensions. So, the relevant intersection would be the inconsistent
![]() $\mathbb {L}_{\mathsf { a}}$
-theory.
$\mathbb {L}_{\mathsf { a}}$
-theory.
We can define the notions “effective
![]() $\mathcal {X}$
-inseparability” and “strong effective
$\mathcal {X}$
-inseparability” and “strong effective
![]() $\mathcal {X}$
-inseparability” in the forms that witnesses can be found from the set
$\mathcal {X}$
-inseparability” in the forms that witnesses can be found from the set
![]() $\mathcal {X}$
. The following theorem is a special case of a theorem proved in our paper [Reference Kurahashi and Visser9].
$\mathcal {X}$
. The following theorem is a special case of a theorem proved in our paper [Reference Kurahashi and Visser9].
Theorem 7.7 (Kurahashi and Visser [Reference Kurahashi and Visser9, Theorem 5.5])
If T is
![]() $\mathsf {coTh}_{T}$
-creative and effectively inseparable, then T is strongly effectively
$\mathsf {coTh}_{T}$
-creative and effectively inseparable, then T is strongly effectively
![]() $\mathsf {coTh}_{T}$
-inseparable.
$\mathsf {coTh}_{T}$
-inseparable.
Since
![]() $\mathsf {R}_0$
is effectively inseparable, every
$\mathsf {R}_0$
is effectively inseparable, every
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theory is also effectively inseparable. Thus, Theorems 7.4 and 7.7 establish the following theorem which is a generalization of Theorem 2.5 and a strengthening of Theorem 7.4.
$\mathsf {R}_{0\mathsf {p}}$
-sourced theory is also effectively inseparable. Thus, Theorems 7.4 and 7.7 establish the following theorem which is a generalization of Theorem 2.5 and a strengthening of Theorem 7.4.
Theorem 7.8. For any
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory T, we have that T is strongly effectively
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory T, we have that T is strongly effectively
![]() $\mathsf {coTh}_{T}$
-inseparable.
$\mathsf {coTh}_{T}$
-inseparable.
Theorem 7.8 is the strongest form of the first incompleteness theorem given in the present paper. Of course, one can prove Theorem 7.8 directly in a similar way as described in the proof of Theorem 2.5 above.
We close this section with the following application of Theorem 7.8.
Definition 7.9. Let T be a c.e.
![]() $\mathcal {L}$
-theory and
$\mathcal {L}$
-theory and
![]() $\mathcal {X}$
be a set of
$\mathcal {X}$
be a set of
![]() $\mathcal {L}$
-sentences. We say that T is effectively uniformly essentially
$\mathcal {L}$
-sentences. We say that T is effectively uniformly essentially
![]() $\mathcal {X}$
-incomplete iff there exists a partial computable function
$\mathcal {X}$
-incomplete iff there exists a partial computable function
![]() $\varPhi $
such that for every computable sequence of consistent c.e. extensions
$\varPhi $
such that for every computable sequence of consistent c.e. extensions
![]() $U_i$
of T with index j, we have that
$U_i$
of T with index j, we have that
![]() $\varPhi (j)$
converges,
$\varPhi (j)$
converges,
![]() $\varPhi (j) \in \mathcal {X}$
, and for all i,
$\varPhi (j) \in \mathcal {X}$
, and for all i,
![]() $U_i \nvdash \varPhi (j)$
and
$U_i \nvdash \varPhi (j)$
and
![]() $U_i \nvdash \neg \, \varPhi (j)$
.
$U_i \nvdash \neg \, \varPhi (j)$
.
We proved in [Reference Kurahashi and Visser9] the following theorem.
Theorem 7.10 (Kurahashi and Visser [Reference Kurahashi and Visser9, Theorem 2.9])
Let T be any c.e.
![]() $\mathcal {L}$
-theory and
$\mathcal {L}$
-theory and
![]() $\mathcal {X}$
be any set of
$\mathcal {X}$
be any set of
![]() $\mathcal {L}$
-sentences. The following are equivalent:
$\mathcal {L}$
-sentences. The following are equivalent:
-
a. T is effectively
 $\mathcal {X}$
-inseparable.
$\mathcal {X}$
-inseparable. -
b. T is effectively uniformly essentially
 $\mathcal {X}$
-incomplete.
$\mathcal {X}$
-incomplete.
By combining this theorem with Theorem 7.8, we obtain the following strengthening of Corollary 7.5.
Corollary 7.11. Every
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory T is effectively uniformly essentially
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory T is effectively uniformly essentially
![]() $\mathsf {coTh}_{T}$
-incomplete.
$\mathsf {coTh}_{T}$
-incomplete.
8 Various facts about degree structures
In this section, we provide various applications of our framework to degrees of interpretability.
8.1 Useful insights
We first remind the reader of a special property of
![]() $\mathsf {R}$
.
$\mathsf {R}$
.
Theorem 8.1 (Visser [Reference Visser21, Theorem 6])
For any c.e. theory T, we have that
![]() $\mathsf {R} \vartriangleright T$
if and only if every finite subtheory of T has a finite model.
$\mathsf {R} \vartriangleright T$
if and only if every finite subtheory of T has a finite model.
We note that this property is inherited by every c.e. theory that is mutually interpretable with
![]() $\mathsf {R}$
.
$\mathsf {R}$
.
We have the following definition.
-
• The theory T is a globalizer iff, for every c.e. theory W, whenever
 $T \rhd _{\mathsf {loc}} W$
, then
$T \rhd _{\mathsf {loc}} W$
, then
 $T \rhd W$
.
$T \rhd W$
.
Examples of globalizers are
![]() $\mathsf {PRA}, \mathsf {PA}$
, and
$\mathsf {PRA}, \mathsf {PA}$
, and
![]() $\mathsf {ZF}$
. Theorem 8.1 has the following useful consequence, which also appears in [Reference Visser21].
$\mathsf {ZF}$
. Theorem 8.1 has the following useful consequence, which also appears in [Reference Visser21].
Theorem 8.2.
![]() $\mathsf {R}$
is a globalizer.
$\mathsf {R}$
is a globalizer.
Proof. Suppose
![]() $\mathsf {R} \rhd _{\mathsf {loc}} U$
. Then, for every finitely axiomatized subtheory
$\mathsf {R} \rhd _{\mathsf {loc}} U$
. Then, for every finitely axiomatized subtheory
![]() $U_0$
of U, we have
$U_0$
of U, we have
![]() $\mathsf {R} \rhd U_0$
. So, for every finitely axiomatized subtheory
$\mathsf {R} \rhd U_0$
. So, for every finitely axiomatized subtheory
![]() $U_0$
of U, there is a finitely axiomatized subtheory A of
$U_0$
of U, there is a finitely axiomatized subtheory A of
![]() $\mathsf {R}$
, such that
$\mathsf {R}$
, such that
![]() $A \rhd U_0$
. Since A has a finite model, so has
$A \rhd U_0$
. Since A has a finite model, so has
![]() $U_0$
. We may conclude that every finitely axiomatized subtheory
$U_0$
. We may conclude that every finitely axiomatized subtheory
![]() $U_0$
of U has a finite model. Ergo,
$U_0$
of U has a finite model. Ergo,
![]() $\mathsf {R} \rhd U$
.
$\mathsf {R} \rhd U$
.
Cobham has shown that
![]() $\mathsf {R}_0$
is mutually interpretable with
$\mathsf {R}_0$
is mutually interpretable with
![]() $\mathsf {R}$
; see [Reference Jones and Shepherdson6]. It follows that the insights contained in Theorems 8.1 and 8.2 are inherited by
$\mathsf {R}$
; see [Reference Jones and Shepherdson6]. It follows that the insights contained in Theorems 8.1 and 8.2 are inherited by
![]() $\mathsf {R}_0$
.
$\mathsf {R}_0$
.
We give two useful results. We assume that we have a
![]() $\Sigma _1$
-representation of interpretability
$\Sigma _1$
-representation of interpretability
![]() $\rhd $
for the case that the interpreted theory is finitely axiomatized and the interpreting theory is computably enumerable. For later use we also assume that this representation is well-behaved. Par abus de langage, we write
$\rhd $
for the case that the interpreted theory is finitely axiomatized and the interpreting theory is computably enumerable. For later use we also assume that this representation is well-behaved. Par abus de langage, we write
![]() $\rhd $
both for the meta-notion and for its theory-internal representation.
$\rhd $
both for the meta-notion and for its theory-internal representation.
Theorem 8.3. Let W be a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory and let A be finitely axiomatized. We can effectively find a
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory and let A be finitely axiomatized. We can effectively find a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\lambda $
from an index of W, such that
$\lambda $
from an index of W, such that
![]() $\mathbb {N} \models \lambda $
,
$\mathbb {N} \models \lambda $
, ![]() , and
, and
![]() $W \rhd A$
are equivalent.
$W \rhd A$
are equivalent.
Proof. Let W be
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced and let A be finitely axiomatized. By Theorem 6.7, we obtain a
$\mathsf {R}_{0\mathsf {p}}$
-sourced and let A be finitely axiomatized. By Theorem 6.7, we obtain a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\lambda $
satisfying the following equivalence:
$\lambda $
satisfying the following equivalence:
Suppose ![]() . Then, we have
. Then, we have
![]() $\mathbb {N} \models \lambda $
and, thus,
$\mathbb {N} \models \lambda $
and, thus, ![]() by Theorem 5.3. Hence,
by Theorem 5.3. Hence,
![]() $W\vartriangleright A$
.
$W\vartriangleright A$
.
Conversely, suppose that
![]() $W \vartriangleright A$
. If
$W \vartriangleright A$
. If
![]() $\mathbb {N} \models \neg \, \lambda $
, then we have
$\mathbb {N} \models \neg \, \lambda $
, then we have ![]() by Theorem 5.3, and, hence,
by Theorem 5.3, and, hence, ![]() . By the fixed point equation, we find
. By the fixed point equation, we find
![]() $\mathbb {N} \models \lambda $
, contradicting our assumption that
$\mathbb {N} \models \lambda $
, contradicting our assumption that
![]() $\mathbb {N} \models \neg \,\lambda $
. So, we may conclude that
$\mathbb {N} \models \neg \,\lambda $
. So, we may conclude that
![]() $\mathbb {N} \models \lambda $
, and, thus,
$\mathbb {N} \models \lambda $
, and, thus, ![]() .
.
Remark 8.4. The proof of Theorem 8.3 is strongly reminiscent of the proof of Löb’s Theorem. Regrettably, it does not seem that we can take the further step to obtain an analog of Löb’s theorem, to wit:
The left-to-right direction is trivial, but we do not know about the right-to-left direction at the moment.
Example 8.5. Juvenal Murwanashyaka asked whether there is a finitely axiomatized theory B that interprets
![]() $\mathsf {VS}$
but does not interpret
$\mathsf {VS}$
but does not interpret
![]() $\mathsf {AS}$
. Theorem 8.3 provides an example that, additionally, is a same-signature extension of
$\mathsf {AS}$
. Theorem 8.3 provides an example that, additionally, is a same-signature extension of
![]() $\mathsf {VS}$
.
$\mathsf {VS}$
.
We can see this as follows. Since
![]() $\mathsf {VS}$
is
$\mathsf {VS}$
is
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced, we have, by Theorem 8.3, a finite same-signature-theory B (
$\mathsf {R}_{0\mathsf {p}}$
-sourced, we have, by Theorem 8.3, a finite same-signature-theory B (![]() , such that
, such that
![]() $B\rhd \mathsf {AS}$
iff
$B\rhd \mathsf {AS}$
iff
![]() $\mathsf {VS} \rhd \mathsf {AS}$
. However,
$\mathsf {VS} \rhd \mathsf {AS}$
. However,
![]() $\mathsf {VS} \mathrel {\not \! \rhd } \mathsf {AS}$
, since, otherwise, a finite subtheory of
$\mathsf {VS} \mathrel {\not \! \rhd } \mathsf {AS}$
, since, otherwise, a finite subtheory of
![]() $\mathsf {VS}$
would interpret
$\mathsf {VS}$
would interpret
![]() $\mathsf {AS}$
. Such finite subtheories are interpretable in the theory of non-surjective pairing, i.e.,
$\mathsf {AS}$
. Such finite subtheories are interpretable in the theory of non-surjective pairing, i.e.,
![]() $\mathsf {VS}0+\mathsf {VS}2$
, and, as is well-known this theory has a decidable extension. On the other hand,
$\mathsf {VS}0+\mathsf {VS}2$
, and, as is well-known this theory has a decidable extension. On the other hand,
![]() $\mathsf {AS}$
is essentially undecidable. Since
$\mathsf {AS}$
is essentially undecidable. Since
![]() $\mathbb {N} \models \neg \lambda $
, we have that B is an extension of
$\mathbb {N} \models \neg \lambda $
, we have that B is an extension of
![]() $\mathsf {VS}$
by Theorem 5.3.
$\mathsf {VS}$
by Theorem 5.3.
Similarly, we can specify a finitely axiomatized same-signature extension of
![]() $\mathsf {PRA}$
that does not interpret
$\mathsf {PRA}$
that does not interpret
![]() $\mathrm I\Sigma _1$
.
$\mathrm I\Sigma _1$
.
Corollary 8.6. Let W be a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory, and let T be any c.e. theory.
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory, and let T be any c.e. theory.
-
i. Suppose
 $W \ntriangleright _{\mathsf {loc}} T$
. Then, there is a false
$W \ntriangleright _{\mathsf {loc}} T$
. Then, there is a false
 $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
 $\lambda $
such that
$\lambda $
such that  .
. -
ii. Suppose W is a globalizer and
 $W \ntriangleright T$
. Then, there is a false
$W \ntriangleright T$
. Then, there is a false
 $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
 $\lambda $
such that
$\lambda $
such that  .
.
Proof. We prove (i). Let W be
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced and let T be any c.e. theory. Suppose
$\mathsf {R}_{0\mathsf {p}}$
-sourced and let T be any c.e. theory. Suppose
![]() $W \ntriangleright _{\mathsf {loc}} T$
. It follows that
$W \ntriangleright _{\mathsf {loc}} T$
. It follows that
![]() $W \ntriangleright A$
, for some finitely axiomatized subtheory A of T. We apply Theorem 8.3 to find a false
$W \ntriangleright A$
, for some finitely axiomatized subtheory A of T. We apply Theorem 8.3 to find a false
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\lambda $
such that
$\lambda $
such that ![]() . It follows that
. It follows that ![]() .
.
(ii) is immediate from (i).
Here is another result in the same spirit as Theorem 8.3 that uses a Rosser argument. We remind the reader of our representation of
![]() $\rhd $
is well-behaved (under the assumption that the interpreted theory is finitely axiomatized and the interpreting theory is c.e.).
$\rhd $
is well-behaved (under the assumption that the interpreted theory is finitely axiomatized and the interpreting theory is c.e.).
Theorem 8.7. Let W be a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theory, let T be a c.e. theory such that
$\mathsf {R}_{0\mathsf {p}}$
-sourced theory, let T be a c.e. theory such that
![]() $T \rhd _{\mathsf {loc}} W$
, and let A be finitely axiomatized. Then, there is a
$T \rhd _{\mathsf {loc}} W$
, and let A be finitely axiomatized. Then, there is a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\theta $
, which is
$\theta $
, which is
![]() $\mathsf {R}_0$
-provably equivalent to a witness comparison sentence, such that the following are equivalent:
$\mathsf {R}_0$
-provably equivalent to a witness comparison sentence, such that the following are equivalent:
-
a.
 or
or  ,
, -
b.
 $ T \vartriangleright A$
.
$ T \vartriangleright A$
.
Proof. Suppose
![]() $T \vartriangleright _{\mathsf {loc}} W$
. By Theorem 6.7, we obtain a
$T \vartriangleright _{\mathsf {loc}} W$
. By Theorem 6.7, we obtain a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\theta $
satisfying the following equivalence:
$\theta $
satisfying the following equivalence:
Clearly (b) implies (a). We show that (a) implies (b). Suppose we have (a). Let ![]() . Clearly, we have
. Clearly, we have
![]() $\mathbb {N} \models \eta $
or
$\mathbb {N} \models \eta $
or
![]() $N \models \eta ^\bot $
.
$N \models \eta ^\bot $
.
Suppose
![]() $\mathbb {N} \models \eta $
. It follows that
$\mathbb {N} \models \eta $
. It follows that
![]() $\mathbb {N} \models \theta $
and
$\mathbb {N} \models \theta $
and ![]() . It follows that
. It follows that ![]() , by Theorem 5.3. Since
, by Theorem 5.3. Since
![]() $T \rhd _{\mathsf {loc}} W$
, we find
$T \rhd _{\mathsf {loc}} W$
, we find ![]() . Hence,
. Hence, ![]() .
.
Suppose
![]() $\mathbb {N} \models \eta ^\bot $
. It follows that
$\mathbb {N} \models \eta ^\bot $
. It follows that ![]() . By Theorem 6.5,
. By Theorem 6.5, ![]() is inconsistent, so
is inconsistent, so ![]() is inconsistent. It also follows from
is inconsistent. It also follows from
![]() $\mathbb {N} \models \eta ^\bot $
that
$\mathbb {N} \models \eta ^\bot $
that ![]() . Hence,
. Hence,
![]() $T\rhd A$
.
$T\rhd A$
.
The following theorem, which is in particular the case where T and A are same-signature-theories of W, can be proved in the same way.
Theorem 8.8. Let W be a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theory, let T be a c.e. theory in the signature of W such that
$\mathsf {R}_{0\mathsf {p}}$
-sourced theory, let T be a c.e. theory in the signature of W such that
![]() $T \supseteq W$
, and let A be finitely axiomatized theory in the signature of W. Then, there is a
$T \supseteq W$
, and let A be finitely axiomatized theory in the signature of W. Then, there is a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\theta $
, which is
$\theta $
, which is
![]() $\mathsf {R}_0$
-provably equivalent to a witness comparison sentence, such that the following are equivalent:
$\mathsf {R}_0$
-provably equivalent to a witness comparison sentence, such that the following are equivalent:
-
a.
 or
or
 $T \vartriangleright B$
, where
$T \vartriangleright B$
, where  .
. -
b.
 $ T \vartriangleright A$
.
$ T \vartriangleright A$
.
8.2 Applications of certified extension
We turn to the consideration of various density results.
Theorem 8.9. Consider c.e. theories T and S such that
![]() $S \ntriangleright _{\mathsf {loc}} T$
. Then, there exists a c.e. theory U such that
$S \ntriangleright _{\mathsf {loc}} T$
. Then, there exists a c.e. theory U such that
![]() $T \vartriangleright U$
and
$T \vartriangleright U$
and
![]() $S \ntriangleright _{\mathsf {loc}} U$
and
$S \ntriangleright _{\mathsf {loc}} U$
and
![]() $U \ntriangleright _{\mathsf {loc}} T$
. Moreover, if
$U \ntriangleright _{\mathsf {loc}} T$
. Moreover, if
![]() $T \rhd S$
, then
$T \rhd S$
, then
![]() $U \rhd S$
and, if
$U \rhd S$
and, if
![]() $T \rhd _{\mathsf {loc}} S$
, then
$T \rhd _{\mathsf {loc}} S$
, then
![]() $U \rhd _{\mathsf {loc}} S$
.
$U \rhd _{\mathsf {loc}} S$
.
Proof. Suppose
![]() $S \ntriangleright _{\mathsf {loc}} T$
. Then, we can find a finite subtheory A of T, such that
$S \ntriangleright _{\mathsf {loc}} T$
. Then, we can find a finite subtheory A of T, such that
![]() $S \ntriangleright A$
. Since
$S \ntriangleright A$
. Since
![]() $S \rhd _{\mathsf {loc}} \mathsf {R}_0$
and
$S \rhd _{\mathsf {loc}} \mathsf {R}_0$
and
![]() $\mathsf {R}_0$
is a
$\mathsf {R}_0$
is a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theory, we can apply Theorem 8.7 to S and A. Let
$\mathsf {R}_{0\mathsf {p}}$
-sourced theory, we can apply Theorem 8.7 to S and A. Let
![]() $\theta $
be the promised
$\theta $
be the promised
![]() $\Sigma _1$
-sentence. Since
$\Sigma _1$
-sentence. Since
![]() $S \ntriangleright A$
, we find
$S \ntriangleright A$
, we find ![]() and
and ![]() .
.
Let ![]() . It is immediate that
. It is immediate that
![]() $T \rhd U$
. Moreover, it is also immediate that, if
$T \rhd U$
. Moreover, it is also immediate that, if
![]() $T\rhd S$
, then
$T\rhd S$
, then
![]() $U\rhd S$
and, if
$U\rhd S$
and, if
![]() $T\rhd _{\mathsf {loc}} S$
, then
$T\rhd _{\mathsf {loc}} S$
, then
![]() $U \vartriangleright _{\mathsf {loc}} S$
.
$U \vartriangleright _{\mathsf {loc}} S$
.
Suppose
![]() $S \vartriangleright _{\mathsf {loc}} U$
. Then,
$S \vartriangleright _{\mathsf {loc}} U$
. Then, ![]() . Quod non. Suppose
. Quod non. Suppose
![]() $U \vartriangleright _{\mathsf {loc}} T$
. Then,
$U \vartriangleright _{\mathsf {loc}} T$
. Then, ![]() . Quod non.
. Quod non.
Question 8.10. The proof of Theorem 8.9, seems to use specific properties of
![]() $\mathsf {R}_0$
. Is there a good way to generalize it?
$\mathsf {R}_0$
. Is there a good way to generalize it?
We have immediately the following corollaries.
Corollary 8.11. Consider c.e. theories S and T. Suppose ![]() . Then, there exists a c.e. theory U such that
. Then, there exists a c.e. theory U such that ![]() .
.
The density of the degrees of local interpretability of c.e. theories was first proved by Jan Mycielski, Pavel Pudlák, and Alan Stern in their classical paper [Reference Mycielski, Pudlák and Stern10, Corollary 6.17].
Corollary 8.12. Consider c.e. theories S and T, where either S is a globalizer or T is finitely axiomatized. Suppose ![]() . Then, there exists a c.e. theory U such that
. Then, there exists a c.e. theory U such that ![]() .
.
Proof. We note that if either S is a globalizer or T is finitely axiomatized, then
![]() $S\rhd _{\mathsf {loc}} T$
iff
$S\rhd _{\mathsf {loc}} T$
iff
![]() $S \rhd T$
.
$S \rhd T$
.
Example 8.13. Consider
![]() $\mathsf {INF}$
the theory in the signature of identity with axioms saying, for each n, that there are at least n elements and
$\mathsf {INF}$
the theory in the signature of identity with axioms saying, for each n, that there are at least n elements and
![]() $\mathsf {TWO}$
the theory in the signature of identity with an axiom saying that there are precisely two elements. Then, we have
$\mathsf {TWO}$
the theory in the signature of identity with an axiom saying that there are precisely two elements. Then, we have ![]() . Every theory that has a finite model is interpretable in
. Every theory that has a finite model is interpretable in
![]() $\mathsf {TWO}$
and every theory that has only infinite models proves
$\mathsf {TWO}$
and every theory that has only infinite models proves
![]() $\mathsf {INF}$
. So, there can be no theory strictly
$\mathsf {INF}$
. So, there can be no theory strictly
![]() $\lhd $
-between
$\lhd $
-between
![]() $\mathsf {TWO}$
and
$\mathsf {TWO}$
and
![]() $\mathsf {INF}$
. Ergo, density fails in general in the degrees of interpretability of c.e. theories.
$\mathsf {INF}$
. Ergo, density fails in general in the degrees of interpretability of c.e. theories.
Problem 8.14. Example 8.13 seems too easy. What if we do have density for all theories with no finite models? So, it would be good to have some further classes of examples.
In one special case, we can constrain the in-between theories a bit more. The following theorem is a generalization of [Reference Visser22, Theorem 2].
Theorem 8.15. Let W be a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory. Consider c.e. theories S and T such that
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory. Consider c.e. theories S and T such that
![]() $W \subseteq S \subseteq T$
and
$W \subseteq S \subseteq T$
and
![]() $S \ntriangleright _{\mathsf {loc}} T$
. Then, there exists a c.e. theory U such that
$S \ntriangleright _{\mathsf {loc}} T$
. Then, there exists a c.e. theory U such that
![]() $S \subseteq U \subseteq T$
and
$S \subseteq U \subseteq T$
and
![]() $S \ntriangleright _{\mathsf {loc}} U$
and
$S \ntriangleright _{\mathsf {loc}} U$
and
![]() $U \ntriangleright _{\mathsf {loc}} T$
.
$U \ntriangleright _{\mathsf {loc}} T$
.
Proof. Suppose W is
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced,
$\mathsf {R}_{0\mathsf {p}}$
-sourced,
![]() $W \subseteq S \subseteq T$
and
$W \subseteq S \subseteq T$
and
![]() $S \ntriangleright _{\mathsf {loc}} T$
. Then, we can find a finite subtheory A of T, such that
$S \ntriangleright _{\mathsf {loc}} T$
. Then, we can find a finite subtheory A of T, such that
![]() $S \ntriangleright A$
. We apply Theorem 8.8 to W,
$S \ntriangleright A$
. We apply Theorem 8.8 to W,
![]() $S \supseteq W$
, and A. Let
$S \supseteq W$
, and A. Let
![]() $\theta $
be the promised
$\theta $
be the promised
![]() $\Sigma _1$
-sentence. Since
$\Sigma _1$
-sentence. Since
![]() $S \ntriangleright A$
, we find
$S \ntriangleright A$
, we find ![]() and
and
![]() $S \ntriangleright B$
, where
$S \ntriangleright B$
, where ![]() .
.
Let
![]() $U : = \{\phi \lor \psi \mid \phi \in T$
and
$U : = \{\phi \lor \psi \mid \phi \in T$
and ![]() . It is immediate that
. It is immediate that
![]() $S \subseteq U \subseteq T$
.
$S \subseteq U \subseteq T$
.
Since B is a finite subtheory of U and
![]() $S \ntriangleright B$
, we have that
$S \ntriangleright B$
, we have that
![]() $S \ntriangleright _{\mathsf {loc}} U$
. Also since
$S \ntriangleright _{\mathsf {loc}} U$
. Also since ![]() and
and ![]() , we have
, we have
![]() $U \ntriangleright _{\mathsf {loc}} T$
.
$U \ntriangleright _{\mathsf {loc}} T$
.
Corollary 8.16. Suppose that W is a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory. Consider c.e. theories S and T such that
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theory. Consider c.e. theories S and T such that
![]() $W \subseteq S \subseteq T$
, where either S is a globalizer or T is finitely axiomatized. Suppose
$W \subseteq S \subseteq T$
, where either S is a globalizer or T is finitely axiomatized. Suppose
![]() $S \ntriangleright T$
. Then, there exists a c.e. theory U such that
$S \ntriangleright T$
. Then, there exists a c.e. theory U such that
![]() $S \subseteq U \subseteq T$
and
$S \subseteq U \subseteq T$
and
![]() $S \ntriangleright U$
and
$S \ntriangleright U$
and
![]() $U \ntriangleright T$
.
$U \ntriangleright T$
.
Theorem 8.17. Any finite theory is the supremum of the finite theories strictly below it in the lattice of the interpretability degrees of c.e. theories.
We will give two proofs. The first uses an ordinary Gödel numbering and the second a self-referential one. We remind the reader that we chose the representation of
![]() $\rhd $
in such a way that, as long as the interpreted theory is finite and the interpreting one c.e., it is well-behaved and 1-
$\rhd $
in such a way that, as long as the interpreted theory is finite and the interpreting one c.e., it is well-behaved and 1-
![]() $\Sigma _1$
.
$\Sigma _1$
.
Proof with ordinary Gödel numbering
Suppose A is a finitely axiomatized theory. If A is in the minimal degree, we are immediately done. Suppose A is non-minimal. Suppose U interprets all finitely axiomatized theories strictly below A. We have to show that
![]() $U \rhd A$
.
$U \rhd A$
.
By Theorem 6.7(ii), we can find
![]() $\Sigma _1$
-sentences
$\Sigma _1$
-sentences
![]() $\rho $
and
$\rho $
and
![]() $\theta $
such that:
$\theta $
such that:
-
•
 .
. -
•
 .
.
Let ![]() .
.
Claim 1. Suppose ![]() . Then,
. Then,
![]() $U \rhd A$
.
$U \rhd A$
.
Proof of Claim 1
Suppose ![]() . Then,
. Then,
![]() $\mathbb {N} \models \eta $
or
$\mathbb {N} \models \eta $
or
![]() $\mathbb {N} \models \eta ^\bot $
. In the first case, we have, by Theorem 6.4, that
$\mathbb {N} \models \eta ^\bot $
. In the first case, we have, by Theorem 6.4, that
![]() $[\theta ]\vdash \bot $
. Hence,
$[\theta ]\vdash \bot $
. Hence,
![]() $U\rhd A$
.
$U\rhd A$
.
In the second case, we have ![]() . By Theorem 6.4, we find
. By Theorem 6.4, we find
![]() $[\rho ]\vdash \bot $
. Hence, again,
$[\rho ]\vdash \bot $
. Hence, again,
![]() $U\rhd A$
.
$U\rhd A$
.
So, in both cases, we may conclude
![]() $U\rhd A$
.
$U\rhd A$
.
Claim 2. Suppose ![]() . Then,
. Then,
![]() $U \rhd A$
.
$U \rhd A$
.
Proof of Claim 2
Suppose ![]() . It follows that
. It follows that
![]() $\mathbb {N} \models \eta $
or
$\mathbb {N} \models \eta $
or
![]() $\mathbb {N} \models \eta ^\bot $
. In the first case it follows that (a)
$\mathbb {N} \models \eta ^\bot $
. In the first case it follows that (a) ![]() or (b)
or (b) ![]() . In subcase (a), we find, by Claim 1, that
. In subcase (a), we find, by Claim 1, that
![]() $U \rhd A$
. In subcase (b), we have
$U \rhd A$
. In subcase (b), we have
![]() $\mathbb {N} \models \rho $
, and, hence, by Theorem 2.9, that
$\mathbb {N} \models \rho $
, and, hence, by Theorem 2.9, that
![]() $\mathsf {R}_0 \vdash [\rho ]$
. So,
$\mathsf {R}_0 \vdash [\rho ]$
. So,
![]() $[\rho ]$
has a finite model, and, thus, A is in the minimal degree, contradicting our assumption on A.
$[\rho ]$
has a finite model, and, thus, A is in the minimal degree, contradicting our assumption on A.
Suppose
![]() $\mathbb {N} \models \eta ^\bot $
. In that case, we have
$\mathbb {N} \models \eta ^\bot $
. In that case, we have ![]() . So, by Theorem 6.4, we find
. So, by Theorem 6.4, we find
![]() $U \rhd A$
.
$U \rhd A$
.
Claim 3. We have either ![]() or
or ![]() .
.
Proof of Claim 3
Suppose we have both ![]() and
and ![]() . Then,
. Then, ![]() . It follows that
. It follows that
![]() $\mathbb {N} \models \eta $
or
$\mathbb {N} \models \eta $
or
![]() $\mathbb {N} \models \eta ^\bot $
, and, hence, that
$\mathbb {N} \models \eta ^\bot $
, and, hence, that
![]() $\mathbb {N} \models \rho $
or
$\mathbb {N} \models \rho $
or
![]() $\mathbb {N} \models \theta $
. In both cases we may conclude that
$\mathbb {N} \models \theta $
. In both cases we may conclude that ![]() has a finite model, so A is in the minimal degree, contradicting our assumption on A.
has a finite model, so A is in the minimal degree, contradicting our assumption on A.
We are now ready to prove the theorem. By Claim 3, one of ![]() and
and ![]() is strictly below A, and, hence, below U. If
is strictly below A, and, hence, below U. If ![]() , it follows by Claim 1 that
, it follows by Claim 1 that
![]() $U\rhd A$
. If
$U\rhd A$
. If ![]() , it follows by Claim 2 that
, it follows by Claim 2 that
![]() $U\rhd A$
. So, A is indeed the supremum of the finite elements strictly below it.
$U\rhd A$
. So, A is indeed the supremum of the finite elements strictly below it.
We now give our proof using a self-referential Gödel numbering. The proof will be largely the same, only we need just one fixed point. We note that e.g., the arithmetized form of
![]() $U \rhd A$
in this proof is the form appropriate for the self-referential Gödel numbering and, thus, is different from the case of the ordinary numbering. We opted to keep the same notations for readability’s sake, but the reader should keep the point in mind.
$U \rhd A$
in this proof is the form appropriate for the self-referential Gödel numbering and, thus, is different from the case of the ordinary numbering. We opted to keep the same notations for readability’s sake, but the reader should keep the point in mind.
Proof with self-referential Gödel numbering
Suppose A is a finitely axiomatized theory. If A is in the minimal degree, we are immediately done. Suppose A is non-minimal. Suppose U interprets all finitely axiomatized theories strictly below A. We have to show that
![]() $U \rhd A$
. We find
$U \rhd A$
. We find
![]() $\rho $
with:
$\rho $
with:
Claim 1. Suppose ![]() . Then,
. Then,
![]() $U \rhd A$
.
$U \rhd A$
.
Proof of Claim 1
Suppose ![]() . Then,
. Then,
![]() $\mathbb {N} \models \rho $
or
$\mathbb {N} \models \rho $
or
![]() $\mathbb {N} \models \rho ^\bot $
. In the first case, we have, by Theorem 6.4, that
$\mathbb {N} \models \rho ^\bot $
. In the first case, we have, by Theorem 6.4, that
![]() $[\rho ^{\bot }]\vdash \bot $
. Hence,
$[\rho ^{\bot }]\vdash \bot $
. Hence,
![]() $U\rhd A$
.
$U\rhd A$
.
In the second case, we have ![]() . By Theorem 6.4, we find
. By Theorem 6.4, we find
![]() $[\rho ]\vdash \bot $
. Hence, again,
$[\rho ]\vdash \bot $
. Hence, again,
![]() $U\rhd A$
.
$U\rhd A$
.
So, in both cases, we may conclude
![]() $U\rhd A$
.
$U\rhd A$
.
Claim 2. Suppose ![]() . Then,
. Then,
![]() $U \rhd A$
.
$U \rhd A$
.
Proof of Claim 2
Suppose ![]() . It follows that
. It follows that
![]() $\mathbb {N} \models \rho $
or
$\mathbb {N} \models \rho $
or
![]() $\mathbb {N} \models \rho ^\bot $
. In the first case it follows that (a)
$\mathbb {N} \models \rho ^\bot $
. In the first case it follows that (a) ![]() or (b)
or (b) ![]() . In subcase (a), we find, by Claim 1, that
. In subcase (a), we find, by Claim 1, that
![]() $U \rhd A$
. In subcase (b), we have
$U \rhd A$
. In subcase (b), we have
![]() $\mathbb {N} \models \rho $
, and, hence, by Theorem 2.9, that
$\mathbb {N} \models \rho $
, and, hence, by Theorem 2.9, that
![]() $\mathsf {R}_0 \vdash [\rho ]$
. So,
$\mathsf {R}_0 \vdash [\rho ]$
. So,
![]() $[\rho ]$
has a finite model, and, thus, A is in the minimal degree, contradicting our assumption on A.
$[\rho ]$
has a finite model, and, thus, A is in the minimal degree, contradicting our assumption on A.
Suppose
![]() $\mathbb {N} \models \rho ^\bot $
. In that case, we have
$\mathbb {N} \models \rho ^\bot $
. In that case, we have ![]() . So, by Theorem 6.4, we find
. So, by Theorem 6.4, we find
![]() $U \rhd A$
.
$U \rhd A$
.
Claim 3. We have either ![]() or
or ![]() .
.
Proof of Claim 3
Suppose we have both ![]() and
and ![]() . Then,
. Then, ![]() . It follows that
. It follows that
![]() $\mathbb {N} \models \rho $
or
$\mathbb {N} \models \rho $
or
![]() $\mathbb {N} \models \rho ^\bot $
. In both cases we may conclude that
$\mathbb {N} \models \rho ^\bot $
. In both cases we may conclude that ![]() has a finite model, so A is in the minimal degree, contradicting our assumption on A.
has a finite model, so A is in the minimal degree, contradicting our assumption on A.
We are now ready to prove the theorem. By Claim 3, one of ![]() and
and ![]() is strictly below A, and, hence, below U. If
is strictly below A, and, hence, below U. If ![]() , it follows by Claim 1 that
, it follows by Claim 1 that
![]() $U\rhd A$
. If
$U\rhd A$
. If ![]() , it follows by Claim 2 that
, it follows by Claim 2 that
![]() $U\rhd A$
. So, A is indeed the supremum of the finite elements strictly below it.
$U\rhd A$
. So, A is indeed the supremum of the finite elements strictly below it.
Example 8.18. We note that both in the local and in the global degrees of interpretability of c.e. theories, the degree of the theory
![]() $\mathsf {INF}$
is not the supremum of the degrees of the theories strictly below them, so a fortiori, it is not the supremum of the degrees of the finitely axiomatizable ones.
$\mathsf {INF}$
is not the supremum of the degrees of the theories strictly below them, so a fortiori, it is not the supremum of the degrees of the finitely axiomatizable ones.
Corollary 8.19. In the lattice of c.e. degrees of interpretability, no theory A can be finitely axiomatized, non-minimal, join-irreducible, and compact.
Proof. Suppose A is finitely axiomatized, non-minimal, join-irreducible, and compact. By Theorem 8.17, A is the supremum of the finitely axiomatized theories strictly below it. Hence, by compactness, it is mutually interpretable with the supremum of a finite number of finite theories strictly below it. By join-irreducibility, it follows that A is mutually interpretable with a finite theory strictly below it. A contradiction.
Theorem 8.20. Consider a c.e. theory W.
-
i. Suppose W is mutually locally interpretable with a
 $\mathsf {R}_{0\mathsf {p}}$
-sourced theory. Then, in the degrees of local interpretability of c.e. theories, W is the infimum of the finitely axiomatized theories above it.
$\mathsf {R}_{0\mathsf {p}}$
-sourced theory. Then, in the degrees of local interpretability of c.e. theories, W is the infimum of the finitely axiomatized theories above it. -
ii. Suppose W is mutually interpretable with a
 $\mathsf {R}_{0\mathsf {p}}$
-sourced globalizer. Then, in the degrees of interpretability of c.e. theories, W is the infimum of the finitely axiomatized theories above it.
$\mathsf {R}_{0\mathsf {p}}$
-sourced globalizer. Then, in the degrees of interpretability of c.e. theories, W is the infimum of the finitely axiomatized theories above it.
Proof. We first prove (i). It is clearly sufficient to prove the result for the case that W is a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theory, for some
$\mathsf {R}_{0\mathsf {p}}$
-sourced theory, for some
![]() $\tau $
. Suppose all finitely axiomatized theories that interpret W locally interpret T. We want to show that
$\tau $
. Suppose all finitely axiomatized theories that interpret W locally interpret T. We want to show that
![]() $W\rhd _{\mathsf {loc}} T$
. Suppose, in order to obtain a contradiction, that
$W\rhd _{\mathsf {loc}} T$
. Suppose, in order to obtain a contradiction, that
![]() $W \ntriangleright _{\mathsf {loc}} T$
. Let
$W \ntriangleright _{\mathsf {loc}} T$
. Let
![]() $\lambda $
be the sentence provided by Corollary 8.6(i) such that
$\lambda $
be the sentence provided by Corollary 8.6(i) such that ![]() . Since
. Since
![]() $\lambda $
is false, we have
$\lambda $
is false, we have ![]() and, hence,
and, hence, ![]() . A contradiction.
. A contradiction.
We turn to (ii). Again is sufficient to prove the result for the case that W is a
![]() $\tau $
-
$\tau $
-
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced theory, for some
$\mathsf {R}_{0\mathsf {p}}$
-sourced theory, for some
![]() $\tau $
. Suppose all finitely axiomatized theories that interpret W interpret T. We want to show that
$\tau $
. Suppose all finitely axiomatized theories that interpret W interpret T. We want to show that
![]() $W\rhd T$
. Suppose, in order to obtain a contradiction, that
$W\rhd T$
. Suppose, in order to obtain a contradiction, that
![]() $W \ntriangleright T$
. Let
$W \ntriangleright T$
. Let
![]() $\lambda $
be the sentence provided by Corollary 8.6(ii) such that
$\lambda $
be the sentence provided by Corollary 8.6(ii) such that ![]() . Since
. Since
![]() $\lambda $
is false, we have
$\lambda $
is false, we have ![]() and, hence,
and, hence, ![]() . A contradiction.
. A contradiction.
Corollary 8.21. Suppose W is mutually interpretable with a c.e. sequential globalizer. Then, W is the interpretability infimum of all finitely axiomatized theories above it (w.r.t.
![]() $\lhd $
).
$\lhd $
).
Proof. Any sequential globalizer U is mutually interpretable with a restricted sequential theory, to wit
![]() $\mho _U$
, which is, of course, itself a globalizer; see [Reference Visser23]. By Corollary 5.11, the theory
$\mho _U$
, which is, of course, itself a globalizer; see [Reference Visser23]. By Corollary 5.11, the theory
![]() $\mho _U$
is a
$\mho _U$
is a
![]() $\mathsf {R}_{0\mathsf {p}}$
-sourced. We now apply Theorem 8.20.
$\mathsf {R}_{0\mathsf {p}}$
-sourced. We now apply Theorem 8.20.
So, e.g.,
![]() $\mathsf {PA}$
is the infimum in the degrees of local interpretability of c.e. theories of the finitely axiomatized theories that locally interpret it.
$\mathsf {PA}$
is the infimum in the degrees of local interpretability of c.e. theories of the finitely axiomatized theories that locally interpret it.
9 Conclusions
We presented the following two new methods.
-
• Certification of
 $\Sigma _1$
-witnesses: We introduced the notion of the certification of an element (Definition 4.1), and explored some consequences of the certification. The certified extension theorem on
$\Sigma _1$
-witnesses: We introduced the notion of the certification of an element (Definition 4.1), and explored some consequences of the certification. The certified extension theorem on
 $\mathsf {R}_0$
(Theorem 2.9) is one of the main results of this study.
$\mathsf {R}_0$
(Theorem 2.9) is one of the main results of this study. -
•
 $\mathsf {R}_{0\mathsf {p}}$
-sourced theories: We developed a generalization of the argument concerning
$\mathsf {R}_{0\mathsf {p}}$
-sourced theories: We developed a generalization of the argument concerning
 $\mathsf {R}_0$
to
$\mathsf {R}_0$
to
 $\mathsf { R}_{0\mathsf {p}}$
-sourced theories, which allows the generalized certified extension theorem (Theorem 5.3) to be applied, for example, to Vaught’s set theory
$\mathsf { R}_{0\mathsf {p}}$
-sourced theories, which allows the generalized certified extension theorem (Theorem 5.3) to be applied, for example, to Vaught’s set theory
 $\mathsf {VS}$
(Theorem 5.6).
$\mathsf {VS}$
(Theorem 5.6).
Our two methods have the following two applications:
-
• Certified
 $\Sigma _1$
-sentences can be successfully applied to provide proofs of Vaught’s two theorems. Furthermore, we proved the strong effective
$\Sigma _1$
-sentences can be successfully applied to provide proofs of Vaught’s two theorems. Furthermore, we proved the strong effective
 $\mathsf {coTh}_{T}$
-inseparability of
$\mathsf {coTh}_{T}$
-inseparability of
 $\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theories, which yields Vaught’s two theorems (Theorem 7.8).
$\mathsf {R}_{0\mathsf {p}}$
-sourced c.e. theories, which yields Vaught’s two theorems (Theorem 7.8). -
• Certified
 $\Sigma _1$
-sentences can also be applied to the study of the degrees of interpretability of theories. We proved some density results (Corollaries 8.12 and 8.16) and studied sufficient conditions for a theory to be the supremum of the theories below it or the infimum of the theories above it (Theorems 8.17 and 8.20).
$\Sigma _1$
-sentences can also be applied to the study of the degrees of interpretability of theories. We proved some density results (Corollaries 8.12 and 8.16) and studied sufficient conditions for a theory to be the supremum of the theories below it or the infimum of the theories above it (Theorems 8.17 and 8.20).
In our paper [Reference Kurahashi and Visser9], we specifically discussed topics related to the first application. This paper may be read in connection with the present paper.
Acknowledgments
We thank the referee for his/her valuable suggestions.
Funding
This work was partly supported by JSPS KAKENHI Grant Numbers JP19K14586 and JP23K03200.