Article contents
Cauchy completeness in elementary logic
Published online by Cambridge University Press: 12 March 2014
Abstract
The inverse of the distance between two structures 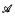 ≢
≢ 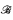 of finite type τ is naturally measured by the smallest integer q such that a sentence of quantifier rank q − 1 is satisfied by
of finite type τ is naturally measured by the smallest integer q such that a sentence of quantifier rank q − 1 is satisfied by 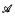 but not by
but not by 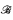 . In this way the space Strτ of structures of type τ is equipped with a pseudometric. The induced topology coincides with the elementary topology of Strτ. Using the rudiments of the theory of uniform spaces, in this elementary note we prove the convergence of every Cauchy net of structures, for any type τ.
. In this way the space Strτ of structures of type τ is equipped with a pseudometric. The induced topology coincides with the elementary topology of Strτ. Using the rudiments of the theory of uniform spaces, in this elementary note we prove the convergence of every Cauchy net of structures, for any type τ.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
REFERENCES
- 1
- Cited by


