Published online by Cambridge University Press: 12 March 2014
§1. A complete atomic modal algebra (CAMA) is a complete atomic Boolean algebra with an additional completely additive unary operator. A (Kripke) frame is just a binary relation on a nonempty set. If 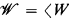 is a frame, then
is a frame, then 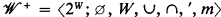 is a CAMA, where mX = {y ∣ (∃x)(y < x Є X)}; and if
is a CAMA, where mX = {y ∣ (∃x)(y < x Є X)}; and if 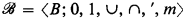 is a CAMA then
is a CAMA then 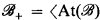 is a frame, where
is a frame, where 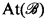 is the set of atoms of
is the set of atoms of 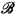 and b1 < b2 ⇔ b1 ∩ mb2 ≠∅.
and b1 < b2 ⇔ b1 ∩ mb2 ≠∅.
Now 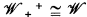 , and
, and 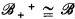 the validity of a modal formula on
the validity of a modal formula on 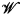 is equivalent to the satisfaction of a modal algebra polynomial identity by
is equivalent to the satisfaction of a modal algebra polynomial identity by 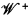 and conversely, so the validity-preserving constructions on frames ought to be in some sense equivalent to the identity-preserving constructions on CAMA's. The former are important for modal logic, and many of the results of universal algebra apply to the latter, so it is worthwhile to fix precisely the sense of the equivalence.
and conversely, so the validity-preserving constructions on frames ought to be in some sense equivalent to the identity-preserving constructions on CAMA's. The former are important for modal logic, and many of the results of universal algebra apply to the latter, so it is worthwhile to fix precisely the sense of the equivalence.
The most important identity-preserving constructions on CAMA's can be described in terms of homomorphisms and complete homomorphisms. Let 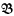 and
and 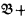 be the categories of CAMA's with homomorphisms and complete homomorphisms, respectively. We shall define categories
be the categories of CAMA's with homomorphisms and complete homomorphisms, respectively. We shall define categories 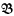 and
and 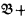 of frames with appropriate morphisms, and show them to be dual respectively to
of frames with appropriate morphisms, and show them to be dual respectively to 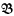 and
and 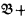 . Then we shall consider certain identity-preserving constructions on CAMA's and attempt to describe the corresponding validity-preserving constructions on frames.
. Then we shall consider certain identity-preserving constructions on CAMA's and attempt to describe the corresponding validity-preserving constructions on frames.
The proofs of duality involve some rather detailed calculations, which have been omitted. All the category theory a reader needs to know is in the first twenty pages of [7].
This work was done while the author was on Sabbatical Leave at the University of Canterbury, Christchurch, and was supported in part by The Canada Council and the National Research Council of Canada.