Article contents
Canonical formulas for K4. Part I: Basic results
Published online by Cambridge University Press: 12 March 2014
Extract
This paper presents a new technique for handling modal logics with transitive frames, i.e. extensions of the modal system K4. In effect, the technique is based on the following fundamental result, to be obtained below in §3.
Given a formula φ, we can effectively construct finite frames 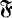 1, …,
1, …, 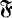 n which completely characterize the set of all transitive general frames refuting φ. More exactly, an arbitrary general frame
n which completely characterize the set of all transitive general frames refuting φ. More exactly, an arbitrary general frame 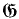 refutes φ iff
refutes φ iff 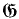 contains a (not necessarily generated) subframe
contains a (not necessarily generated) subframe 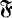 such that (1)
such that (1) 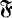 i, for some i ϵ {1, …, n}, is a p-morphic image of
i, for some i ϵ {1, …, n}, is a p-morphic image of 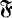 (after Fine [1985] we say
(after Fine [1985] we say 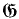 is subreducible to
is subreducible to 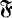 i), (2)
i), (2) 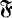 is cofinal in
is cofinal in 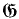 , and (3) every point in
, and (3) every point in 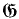 that is not in
that is not in 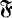 does not get into “closed domains” which are uniquely determined in
does not get into “closed domains” which are uniquely determined in 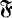 i, by φ.
i, by φ.
This purely technical result has, as it turns out, rather unexpected and profound consequences. For instance, it follows at once that if φ determines no closed domains in the frames 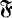 1, …,
1, …, 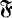 n associated with it, then the normal extension of K4 generated by φ has the finite model property and so is decidable. Moreover, every normal logic axiomatizable by any (even infinite) set of such formulas φ also has the finite model property. This observation would not possibly merit any special attention, were it not for the fact that the class of such logics contains almost all the standard systems within the field of K4 (at least all those mentioned by Segerberg [1971] or Bull and Segerberg [1984]), all logics containing S4.3, all subframe logics of Fine [1985], and a continuum of other logics as well.
n associated with it, then the normal extension of K4 generated by φ has the finite model property and so is decidable. Moreover, every normal logic axiomatizable by any (even infinite) set of such formulas φ also has the finite model property. This observation would not possibly merit any special attention, were it not for the fact that the class of such logics contains almost all the standard systems within the field of K4 (at least all those mentioned by Segerberg [1971] or Bull and Segerberg [1984]), all logics containing S4.3, all subframe logics of Fine [1985], and a continuum of other logics as well.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 35
- Cited by


