Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-22T20:26:15.384Z Has data issue: false hasContentIssue false
  • English
  • Français

A boundedness theorem in ID1(W)

Published online by Cambridge University Press:  12 March 2014

Gerhard Jäger
Gerhard Jäger*
Affiliation:
Mathematik, Eth-Zentrum, Zürich, Switzerland
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we prove a boundedness theorem in the theory ID1(W). This answers a question asked by Feferman, for example in [3]. The background is the following.

Let A[X, x] be an X-positive formula arithmetic in X. The theory ID1(PA) is an extension of Peano arithmetic PA by the following axioms:

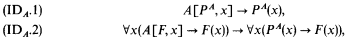
for arbitrary formulas F; PA is a constant for the least fixed point of A[X, x]. Set-theoretically, PA can be defined by recursion on the ordinals as follows:

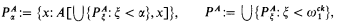
where 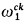is the first nonrecursive ordinal.

Now let a ≺ b be the arithmetic relation which expresses that the recursive tree coded by a is a proper subtree of the tree coded by b, and define

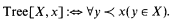
The least fixed point of Tree[X, x] is the set PTree of all well-founded recursive trees. We write W or Wα for PTree or 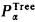, respectively. Since W is 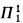complete we have 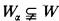for all α < 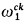. If we define for each element a ∈ W its inductive norm ∣a∣ by ∣a∣≔ min{ξ: a ∈ Wξ}, then we have 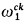= {∣a∣: a ∈ W} and the elements of W can be used as codes for the ordinals less than .

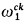Assume that B[X, x] is an X-positive formula arithmetic in X with the only free variables X and x, and assume that QB is a relation that satisfies

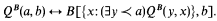
If we define

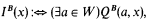
then we obviously have PB = IB.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 4 , December 1986 , pp. 942 - 947
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buchholz, W., Feferman, S., Pohlers, W. and Sieg, W., Iterated inductive definitions and subsystems of analysis: recent proof-theoretical studies, Lecture Notes in Mathematics, vol. 897, Springer-Verlag, Berlin, 1981.Google Scholar
[2]Feferman, S., Formal theories for transfinite iterations of generalized inductive definitions and subsystems of analysis, Intuitionism and proof theory, North-Holland, Amsterdam, 1970, pp. 303–326.Google Scholar
[3]Feferman, S., Monotone inductive definitions, The L. E. J. Brouwer centenary symposium, North-Holland, Amsterdam, 1982, pp. 77–89.Google Scholar
[4]Kreisel, G., The axiom of choice and the class of hyperarithmetic functions, Indagationes Mathematicae, vol. 24 (1962), pp. 307–319.CrossRefGoogle Scholar
[5]Shoenfield, J., Mathematical logic, Addison-Wesley, Reading, Massachusetts, 1967.Google Scholar
[6]Tait, W. W., Applications of the cut elimination theorem to some subsystems of classical analysis, Intuitionism and proof theory, North-Holland, Amsterdam, 1970, pp. 475–488.Google Scholar