Article contents
Boolean algebras and orbits of the lattice of r.e sets modulo the finite sets
Published online by Cambridge University Press: 12 March 2014
Extract
An important program in the study of the structure 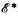 the lattice of r.e. sets modulo finite sets, is the classification of the orbits under Aut(
the lattice of r.e. sets modulo finite sets, is the classification of the orbits under Aut(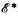 ), the automorphism group of
), the automorphism group of 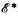 , If Φ ∈ Aut(
, If Φ ∈ Aut(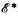 ) and Φ(We) =* Wh(e) for all e ∈ ω, then h is called a presentation of Φ. Define Autχ(
) and Φ(We) =* Wh(e) for all e ∈ ω, then h is called a presentation of Φ. Define Autχ(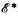 ) to be the class of those elements of Aut(
) to be the class of those elements of Aut(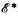 ) that have a presentation in the class of functions X, where for instance X might be the class of Δn functions for n ∈ ω. If Φ ∈ Autx(
) that have a presentation in the class of functions X, where for instance X might be the class of Δn functions for n ∈ ω. If Φ ∈ Autx(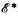 ) then we will say that Φ is an X-automorphism. Note that we only need to consider Δn- and Πn-orbits and automorphisms since if f is a Σn-presentation, then f is a total function and therefore Δn.
) then we will say that Φ is an X-automorphism. Note that we only need to consider Δn- and Πn-orbits and automorphisms since if f is a Σn-presentation, then f is a total function and therefore Δn.
Definition. If X is a class of functions and  ⊆ {Wi: i < ω}, then
⊆ {Wi: i < ω}, then  is an X-orbit iff
is an X-orbit iff  is an orbit under Aut(
is an orbit under Aut(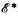 ) and for all A, B ∈
) and for all A, B ∈  there is a Φ ∈ Autx(
there is a Φ ∈ Autx(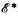 ) satisfying Φ(A) =* B. (Here Φ:
) satisfying Φ(A) =* B. (Here Φ: 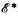 →
→ 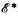 .)
.)
Harrington proved that the creative sets form a Δ0-orbit and Soare proved that the maximal sets form Δ3-orbit. We will show that there is no Boolean algebra 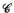 such that {A: A is r.e. and ℒ*(A) ≈
such that {A: A is r.e. and ℒ*(A) ≈ 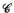 ] forms a Δ2-orbit, where ℒ*(A) is the principal filter of A in
] forms a Δ2-orbit, where ℒ*(A) is the principal filter of A in 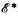 ; ℒ*(A) = {B: B ⊆* A & B ∈
; ℒ*(A) = {B: B ⊆* A & B ∈ 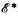 }. The idea behind the proof of this theorem is very similar to the proof by Soare that maximal sets do not form a Δ2-orbit (see Soare [1974] or Soare [1987]).
}. The idea behind the proof of this theorem is very similar to the proof by Soare that maximal sets do not form a Δ2-orbit (see Soare [1974] or Soare [1987]).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
REFERENCES
- 1
- Cited by


