No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
The aim of this paper is to extend the Bass-Milnor-Serre theorem to the nonstandard rings associated with nonstandard models of Peano arithmetic, in brief to Peano rings.
First, we recall the classical setting. Let k be an algebraïc number field, and let θ be its ring of integers. Let n be an integer ≥ 3, and let G be the group Sln(θ) of (n, n) matrices of determinant 1 with coefficients in θ.
The profinite topology in G is the topology having as fundamental system of open subgroups the subgroups of finite index.
Congruence subgroups of finite index of G are the kernels of the maps Sln(θ) → Sln(θ/I) for which all ideals I of θ are of finite index. By taking these subgroups as a fundamental system of open subgroups, one obtains the congruence topology on G. Every open set for this topology is open in the profinite topology.
We denote by Ḡ (resp., Ĝ) the completion of G for the congruence (resp., profinite) topology.
The Bass-Milnor-Serre theorem [1] consists of the two following statements:
(A) If k admits a real embedding, then we have an exact sequence
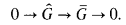
That is, Ĝ and Ḡ are isomorphic.
(B) If k is totally imaginary, then one has an exact sequence
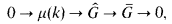
where μ(k)is the group of the roots of unity of k.