Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-31T19:29:58.115Z Has data issue: false hasContentIssue false
  • English
  • Français

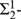BASIS THEOREMS FOR ${\rm{\Sigma }}_2^1$-SETS

Published online by Cambridge University Press:  11 February 2019

CHI TAT CHONG ,
LIUZHEN WU  and
LIANG YU
CHI TAT CHONG
Affiliation:
DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE NATIONAL UNIVERSITY OF SINGAPORE SINGAPORE 119076, SINGAPOREE-mail: [email protected]
LIUZHEN WU
Affiliation:
HLM, ACADEMY OF MATHEMATICS AND SYSTEMS SCIENCE CHINESE ACADEMY OF SCIENCES, EAST ZHONG GUAN CUN ROAD N0. 55 BEIJING 100190, CHINAE-mail: [email protected]
LIANG YU
Affiliation:
DEPARTMENT OF MATHEMATICS NANJING UNIVERSITY, JIANGSU PROVINCE210093P. R. OF CHINAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the following two basis theorems for 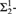${\rm{\Sigma }}_2^1$-sets of reals:

  1. (1) Every nonthin 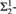${\rm{\Sigma }}_2^1$-set has a perfect 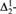${\rm{\Delta }}_2^1$-subset if and only if it has a nonthin 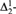${\rm{\Delta }}_2^1$-subset, and this is equivalent to the statement that there is a nonconstructible real.

  2. (2) Every uncountable 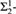${\rm{\Sigma }}_2^1$-set has an uncountable 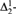${\rm{\Delta }}_2^1$-subset if and only if either every real is constructible or 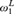$\omega _1^L$ is countable.

We also apply the method that proves (2) to show that if there is a nonconstructible real, then there is a perfect 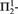${\rm{\Pi }}_2^1$-set with no nonempty 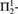${\rm{\Pi }}_2^1$-thin subset, strengthening a result of Harrington [4].

Keywords

03D3003D6003D6503E1503E35basis theoremShoenfield absolutenessconstructibilitypointed treesperfect set
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 376 - 387
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Boolos, G. and Putnam, H., Degrees of unsolvability of constructible sets of integers, this Journal, vol. 33 (1968), pp. 497–513.Google Scholar
Chong, C. T. and Yu, L., Recursion Theory, Computational Aspects of Definability, De Gruyter Series in Logic and its Applications, vol. 8, De Gruyter, Berlin, 2015.10.1515/9783110275643CrossRefGoogle Scholar
Groszek, M. J. and Slaman, T. A., A basis theorem for perfect sets. Bulletin of Symbolic Logic , vol. 4 (1998), no. 2, pp. 204–209.10.2307/421023CrossRefGoogle Scholar
Harrington, L., ${\rm{\Pi }}_2^1$ sets and ${\rm{\Pi }}_2^1$ singletons. Proceedings of the American Mathematical Society, vol. 52 (1975), pp. 356–360.Google Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Jensen, R. B., The fine structure of the constructible hierarchy. Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308; erratum, ibid. 4 (1972), 443, with a section by Jack Silver.10.1016/0003-4843(72)90001-0CrossRefGoogle Scholar
Mansfield, R., Perfect subsets of definable sets of real numbers. Pacific Journal of Mathematics, vol. 35 (1970), pp. 451–457.10.2140/pjm.1970.35.451CrossRefGoogle Scholar
Martin, D. A., The axiom of determinateness and reduction principles in the analytical hierarchy. Bulletin of the American Mathematical Society, vol. 74 (1968), pp. 687–689.10.1090/S0002-9904-1968-11995-0CrossRefGoogle Scholar
Martin, D. A., Proof of a conjecture of Friedman. Proceedings of the American Mathematical Society, vol. 55 (1976), no. 1, p. 129.10.1090/S0002-9939-1976-0406785-9CrossRefGoogle Scholar
Sacks, G. E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.10.1007/978-3-662-12013-2CrossRefGoogle Scholar
Simpson, S. G., Minimal covers and hyperdegrees. Transactions of the American Mathematical Society, vol. 209 (1975), pp. 45–64.10.1090/S0002-9947-1975-0392534-3CrossRefGoogle Scholar
Solovay, R. M., On the cardinality of ${\rm{\Delta }}_2^1$ sets of reals, Foundations of Mathematics (Symposium Commemorating Kurt Gödel, Columbus, Ohio, 1966) (Bulloff, J. J., Holyoke, T. C., and Hahn, S. W., editors), Springer, New York, 1969, pp. 58–73.Google Scholar