Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T22:46:40.228Z Has data issue: false hasContentIssue false
  • English
  • Français

The Baire category theorem in weak subsystems of second-order arithmetic

Published online by Cambridge University Press:  12 March 2014

Douglas K. Brown  and
Stephen G. Simpson
Douglas K. Brown
Affiliation:
Department of Mathematics, Pennsylvania State University, Altoona, Pennsylvania16601
Stephen G. Simpson
Affiliation:
Department of Mathematics, Pennsylvania State University, University Park, Pennsylvania16802
Get access Rights & Permissions [Opens in a new window]

Abstract

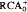Working within weak subsystems of second-order arithmetic Z2 we consider two versions of the Baire Category theorem which are not equivalent over the base system RCA0. We show that one version (B.C.T.I) is provable in RCA0 while the second version (B.C.T.II) requires a stronger system. We introduce two new subsystems of Z2, which we call and , and 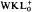, show that 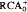suffices to prove B.C.T.II. Some model theory of 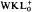and its importance in view of Hilbert's program is discussed, as well as applications of our results to functional analysis.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 2 , June 1993 , pp. 557 - 578
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Blass, A., Hirst, J., and Simpson, S. G., Logical analysis of some theorems of combinatorics and topological dynamics, Logic and combinatorics (Simpson, S. G., editor), Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, RI, 1986.Google Scholar
[2]Brown, D. K., Functional analysis in weak subsystems of second order arithmetic, Ph.D. Thesis, The Pennsylvania State University, University Park, PA, 1987.Google Scholar
[3]Brown, D. K., Notions of closed subsets of a complete separable metric space in weak subsystems of second order arithmetic, Contemporary Mathematics, vol. 106, American Mathematical Society, Providence, RI, 1990, pp. 39–50.Google Scholar
[4]Brown, D. K. and Simpson, S. G., Which set existence axioms are needed to prove the separable Hahn-Banach theorem?, Annals of Pure and Applied Logic, vol. 31 (1986), pp. 123–144.CrossRefGoogle Scholar
[5]Friedman, H., Some systems of second order arithmetic and their use, Proceedings of the International Congress of Mathematicians (Vancouver, 1974), vol. 1, Canadian Mathematical Congress, 1975, pp. 235–242.Google Scholar
[6]Friedman, H., Systems of second order arithmetic with restricted induction, this Journal, vol. 41 (1976), pp. 557–559. (Abstract)Google Scholar
[7]Friedman, H. and Hirst, J., Weak comparability of well orderings and reverse mathematics, Annals of Pure and Applied Logic, vol. 47 (1990), pp. 11–29.CrossRefGoogle Scholar
[8]Friedman, H., Simpson, S. G., and Smith, R., Countable algebra and set existence axioms, Annals of Pure and Applied Logic, vol. 25 (1983), pp. 141–181.CrossRefGoogle Scholar
[9]Hirst, J., Combinatorics in subsystems of second order arithmetic, Ph.D. Thesis, The Pennsylvania State University, University Park, PA, 1987.Google Scholar
[10]Jockush, C. and Soare, R., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[11]Kirby, L. and Paris, J., Initial segments of models of Peano's axioms, Set theory and hierarchy theory V(Bierutowice, Poland, 1976), Springer Lecture Notes in Mathematics, vol. 619, Springer-Verlag, Berlin and New York, 1977, pp. 211–226.CrossRefGoogle Scholar
[12]Kleene, S., Introduction to metamathematics, Van Nostrand, Princeton, NJ, 1952.Google Scholar
[13]Lerman, , Degrees of unsolvability, Springer-Verlag, Berlin and New York, 1983.CrossRefGoogle Scholar
[14]Royden, H. L., Real analysis (second editor), MacMillan, New York, 1968.Google Scholar
[15]Scott, D., Algebras of sets binumerable in complete extensions of arithmetic, Proceedings of Symposia in Pure Mathematics, vol. 5, American Mathematical Society, Providence, RI, 1962, pp. 117–121.Google Scholar
[16]Scott, D. and Tennenbaum, S., On the degrees of complete extensions of arithmetic, Notices of the American Mathematical Society, vol. 7 (1960), pp. 242–243. (Abstract)Google Scholar
[17]Shoenfield, J., On degrees of unsolvability, Annals of Mathematics, vol. 69 (1955), pp. 644–653.CrossRefGoogle Scholar
[18]Sieg, W., Fragments of arithmetic, Annals of Pure and Applied Logic, vol. 28 (1985), pp. 33–72.CrossRefGoogle Scholar
[19]Simpson, S. G., Partial realizations of Hilbert's program, this Journal, vol. 53 (1988), pp. 349–363.Google Scholar
[20]Simpson, S. G., and transfinite induction, Logic Colloquiu '80 (vanDalen, D., editor), North-Holland, Amsterdam, 1982.Google Scholar
[21]Simpson, S. G., Subsystems of second order arithmetic, in preparation.Google Scholar
[22]Simpson, S. G., Which set existence axioms are needed to prove the Cauchy-Peano theorem for ordinary differential equations?, this Journal, vol. 49 (1984), pp. 783–802.Google Scholar
[23]Simpson, S. G. and Smith, R., Factorization of polynomials and induction, Annals of Pure and Applied Logic, vol. 31 (1986), pp. 289–306.CrossRefGoogle Scholar
[24]Tait, W. W., Finitism, Journal of Philosophy, vol. 78 (1981), pp. 524–546.CrossRefGoogle Scholar
[25]Weyl, H., Das Kontinuum: Kritische Untersuchungen über die Grundlagen der Analysis (Berlin, 1917, iv + 84 pages), reprinted by Chelsea, New York, 1960 and 1973.Google Scholar
[26]Yu, X., Measure theory in weak subsystems of second order arithmetic, Ph.D. Thesis, The Pennsylvania State University, University Park, PA, 1987.Google Scholar