Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Borovik, A. V.
1995.
Finite and Locally Finite Groups.
p.
247.
Altınel, Tuna
Borovik, Alexandre
and
Cherlin, Gregory
1997.
Groups of Mixed Type.
Journal of Algebra,
Vol. 192,
Issue. 2,
p.
524.
Wagner, Frank O.
1997.
On the structure of stable groups.
Annals of Pure and Applied Logic,
Vol. 89,
Issue. 1,
p.
85.
Jaligot, Eric
1999.
Groupes de type mixte.
Journal of Algebra,
Vol. 212,
Issue. 2,
p.
753.
Wagner, Frank
2000.
Vol. 2,
Issue. ,
p.
277.
Jaligot, Eric
2001.
Full Frobenius Groups of Finite Morley Rank and the Feit-Thompson Theorem.
Bulletin of Symbolic Logic,
Vol. 7,
Issue. 3,
p.
315.
Cherlin, Gregory
and
Jaligot, Eric
2004.
Tame minimal simple groups of finite Morley rank.
Journal of Algebra,
Vol. 276,
Issue. 1,
p.
13.
Frécon, Olivier
2006.
Around unipotence in groups of finite Morley rank.
jgth,
Vol. 9,
Issue. 3,
p.
341.
Frécon, Olivier
2017.
Simple groups of Morley rank 3 are algebraic.
Journal of the American Mathematical Society,
Vol. 31,
Issue. 3,
p.
643.
Poizat, Bruno
2018.
Milieu et symétrie, une étude de la convexité dans les groupes sans involutions.
Journal of Algebra,
Vol. 497,
Issue. ,
p.
143.
Deloro, Adrien
and
Wiscons, Joshua
2020.
The geometry of involutions in ranked groups with ati‐subgroup.
Bulletin of the London Mathematical Society,
Vol. 52,
Issue. 3,
p.
411.
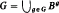 , NG(B) = B, and G has no involutions.
, NG(B) = B, and G has no involutions.