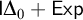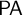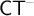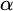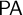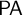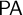1 Introduction
Logicians have long known that different sets of axioms can have the same deductive closure and yet their arithmetizations might exhibit marked differences, e.g., by Craig’s trick every recursively enumerable set of axioms is deductively equivalent to a primitive recursive set of axioms. Feferman’s pivotal paper [Reference Feferman8] on the arithmetization of metamathematics revealed many other dramatic instances of this phenomenon relating to Peano Arithmetic. Let
![]() ${\textsf {PA}}$
be the usual axiomatization of Peano Arithmetic obtained by augmenting
${\textsf {PA}}$
be the usual axiomatization of Peano Arithmetic obtained by augmenting
![]() ${\textsf {Q}}$
(Robinson Arithmetic) with the induction scheme, and consider the theory that has come to be known as Feferman Arithmetic, which we will denote by
${\textsf {Q}}$
(Robinson Arithmetic) with the induction scheme, and consider the theory that has come to be known as Feferman Arithmetic, which we will denote by
![]() $\mathsf {FA}$
. The axioms of
$\mathsf {FA}$
. The axioms of
![]() $\mathsf {FA}$
are obtained by an infinite recursive process of “weeding out” applied to
$\mathsf {FA}$
are obtained by an infinite recursive process of “weeding out” applied to
![]() ${\textsf {PA}}$
as follows: enumerate the proofs of
${\textsf {PA}}$
as follows: enumerate the proofs of
![]() ${\textsf {PA}}$
until a proof of
${\textsf {PA}}$
until a proof of
![]() $0=1$
is arrived, and then discard the largest axiom used in deriving
$0=1$
is arrived, and then discard the largest axiom used in deriving
![]() $0=1$
; we then proceed to enumerate proofs using only axioms of
$0=1$
; we then proceed to enumerate proofs using only axioms of
![]() ${\textsf {PA}}$
smaller than the one discarded. If we arrive at another proof of
${\textsf {PA}}$
smaller than the one discarded. If we arrive at another proof of
![]() $0=1$
from the reduced axiom system, we proceed in the same manner. By definition,
$0=1$
from the reduced axiom system, we proceed in the same manner. By definition,
![]() $\mathsf {FA}$
consists of the axioms of
$\mathsf {FA}$
consists of the axioms of
![]() ${\textsf {PA}}$
that remain upon the completion of this recursive infinite process. Thus
${\textsf {PA}}$
that remain upon the completion of this recursive infinite process. Thus
![]() $\mathsf {FA} = {\textsf {PA}}$
in a sufficiently strong metatheory that can prove the consistency of
$\mathsf {FA} = {\textsf {PA}}$
in a sufficiently strong metatheory that can prove the consistency of
![]() ${\textsf {PA}}$
.Footnote
1
However, the consistency of
${\textsf {PA}}$
.Footnote
1
However, the consistency of
![]() $\mathsf {FA}$
is built into its definition and
$\mathsf {FA}$
is built into its definition and
![]() ${\textsf {PA}}$
can readily verify this fact; thus the equality of
${\textsf {PA}}$
can readily verify this fact; thus the equality of
![]() $\mathsf {FA}$
and
$\mathsf {FA}$
and
![]() ${\textsf {PA}}$
is not provable in
${\textsf {PA}}$
is not provable in
![]() ${\textsf {PA}}$
even though this equality is provable in a sufficiently strong metatheory.
${\textsf {PA}}$
even though this equality is provable in a sufficiently strong metatheory.
In this paper we employ the lens provided by formal truth theory to study axiomatizations of
![]() ${\textsf {PA}}$
. Our focus is on two types of axiomatizations, namely: (1) schematic axiomatizations that are deductively equivalent to
${\textsf {PA}}$
. Our focus is on two types of axiomatizations, namely: (1) schematic axiomatizations that are deductively equivalent to
![]() ${\textsf {PA}}$
, and (2) axiomatizations that are proof-theoretically equivalent to the canonical axiomatization of
${\textsf {PA}}$
, and (2) axiomatizations that are proof-theoretically equivalent to the canonical axiomatization of
![]() ${\textsf {PA}}$
. More specifically, let Elementary Arithmetic (
${\textsf {PA}}$
. More specifically, let Elementary Arithmetic (
![]() ${\textsf {EA}}$
) be the fragment
${\textsf {EA}}$
) be the fragment
![]() $\mathsf {I}\Delta _0 + \mathsf {Exp}$
of
$\mathsf {I}\Delta _0 + \mathsf {Exp}$
of
![]() ${\textsf {PA}}$
, and
${\textsf {PA}}$
, and
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
be the extension of
${\textsf {CT}}^-[{\textsf {EA}}]$
be the extension of
![]() ${\textsf {EA}}$
by the commonly studied axioms of compositional truth
${\textsf {EA}}$
by the commonly studied axioms of compositional truth
![]() ${\textsf {CT}}^-$
(as in Definition 3). We investigate the family of first order theories of the form
${\textsf {CT}}^-$
(as in Definition 3). We investigate the family of first order theories of the form
![]() ${\textsf {CT}}^-[{\textsf {EA}}] +\alpha $
, where
${\textsf {CT}}^-[{\textsf {EA}}] +\alpha $
, where
![]() $\alpha $
either uses a schematic description of
$\alpha $
either uses a schematic description of
![]() ${\textsf {PA}}$
to express “
${\textsf {PA}}$
to express “
![]() ${\textsf {PA}}$
is true,” or
${\textsf {PA}}$
is true,” or
![]() $\alpha $
uses a proof-theoretically equivalent formulation of
$\alpha $
uses a proof-theoretically equivalent formulation of
![]() ${\textsf {PA}}$
to express “
${\textsf {PA}}$
to express “
![]() ${\textsf {PA}}$
is true” (in the sense of Definition 16).
${\textsf {PA}}$
is true” (in the sense of Definition 16).
Several problems can be posed about the aforementioned finitely axiomatized theories of the form
![]() ${\textsf {CT}}^-[{\textsf {EA}}] +\alpha $
, the most prominent of which is the determination of their position with respect to the Tarski Boundary, i.e., the boundary that demarcates the territory of truth theories that are conservative over
${\textsf {CT}}^-[{\textsf {EA}}] +\alpha $
, the most prominent of which is the determination of their position with respect to the Tarski Boundary, i.e., the boundary that demarcates the territory of truth theories that are conservative over
![]() ${\textsf {PA}}$
.Footnote
2
For example, the pioneering work of [Reference Kotlarski, Krajewski and Lachlan14] shows that
${\textsf {PA}}$
.Footnote
2
For example, the pioneering work of [Reference Kotlarski, Krajewski and Lachlan14] shows that
![]() ${\textsf {CT}}^-[{\textsf {EA}}] +\alpha _1 $
is on the conservative side of the Tarski Boundary, where
${\textsf {CT}}^-[{\textsf {EA}}] +\alpha _1 $
is on the conservative side of the Tarski Boundary, where
![]() $\alpha _1$
is the sentence that expresses “each instance of the induction scheme is true” (see Definition 7). On the other hand, let
$\alpha _1$
is the sentence that expresses “each instance of the induction scheme is true” (see Definition 7). On the other hand, let
where
![]() ${\textsf {Con}}(\underline {n})$
is the arithmetical sentence that expresses “there is no proof of inconsistency of
${\textsf {Con}}(\underline {n})$
is the arithmetical sentence that expresses “there is no proof of inconsistency of
![]() ${\textsf {PA}}$
whose code is below n” and
${\textsf {PA}}$
whose code is below n” and
![]() $\omega $
is the set of natural numbers. It is easy to see that
$\omega $
is the set of natural numbers. It is easy to see that
![]() ${\textsf {PA}}^+$
is deductively equivalent to
${\textsf {PA}}^+$
is deductively equivalent to
![]() ${\textsf {PA}}$
(provably in
${\textsf {PA}}$
(provably in
![]() ${\textsf {EA}}$
). However, if we consider a natural arithmetical definition of
${\textsf {EA}}$
). However, if we consider a natural arithmetical definition of
![]() ${\textsf {PA}}^+$
, call it
${\textsf {PA}}^+$
, call it
![]() $\delta (x)$
, and then we choose
$\delta (x)$
, and then we choose
![]() $\alpha _2$
to be the sentence
$\alpha _2$
to be the sentence
then
![]() ${\textsf {CT}}^{-}[{\textsf {EA}}] + \alpha _2$
is on the nonconservative side of the Tarski Boundary since
${\textsf {CT}}^{-}[{\textsf {EA}}] + \alpha _2$
is on the nonconservative side of the Tarski Boundary since
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + \alpha _2$
can prove the consistency of
${\textsf {CT}}^-[{\textsf {EA}}] + \alpha _2$
can prove the consistency of
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
We now briefly discuss the highlights of the paper. In Theorem 26 we show that the set
![]() $\mathsf {Cons}$
consisting of the (codes of) sentences
$\mathsf {Cons}$
consisting of the (codes of) sentences
![]() $\alpha $
such that
$\alpha $
such that
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + \alpha $
is conservative over
${\textsf {CT}}^-[{\textsf {EA}}] + \alpha $
is conservative over
![]() ${\textsf {PA}}$
is
${\textsf {PA}}$
is
![]() $\Pi _2$
-complete; which shows, a fortiori, that the collection of sentences
$\Pi _2$
-complete; which shows, a fortiori, that the collection of sentences
![]() $\alpha $
such that
$\alpha $
such that
![]() ${\textsf {CT}}^-[{\textsf {EA}}] +\alpha $
is conservative over
${\textsf {CT}}^-[{\textsf {EA}}] +\alpha $
is conservative over
![]() ${\textsf {PA}}$
is not recursively enumerable. Another main result of the paper pertains to the strengthening
${\textsf {PA}}$
is not recursively enumerable. Another main result of the paper pertains to the strengthening
![]() ${\textsf {CT}}_{0}$
of
${\textsf {CT}}_{0}$
of
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
obtained by augmenting
${\textsf {CT}}^-[{\textsf {EA}}]$
obtained by augmenting
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
with the scheme of
${\textsf {CT}}^-[{\textsf {EA}}]$
with the scheme of
![]() $\Delta _0$
-induction (in the extended language containing the truth predicate). It is known that the arithmetical strength of
$\Delta _0$
-induction (in the extended language containing the truth predicate). It is known that the arithmetical strength of
![]() ${\textsf {CT}}_0$
far surpasses that of
${\textsf {CT}}_0$
far surpasses that of
![]() ${\textsf {PA}}$
, e.g.,
${\textsf {PA}}$
, e.g.,
![]() ${\textsf {CT}}_0$
can prove
${\textsf {CT}}_0$
can prove
![]() ${\textsf {Con}}_{{\textsf {PA}}}$
,
${\textsf {Con}}_{{\textsf {PA}}}$
,
![]() ${\textsf {Con}}_{{\textsf {PA}} + {\textsf {Con}}_{{\textsf {PA}}}}$
, etc. (see Theorem 6). In Theorem 42 we show that given any r.e. extension U of
${\textsf {Con}}_{{\textsf {PA}} + {\textsf {Con}}_{{\textsf {PA}}}}$
, etc. (see Theorem 6). In Theorem 42 we show that given any r.e. extension U of
![]() ${\textsf {PA}}$
such that
${\textsf {PA}}$
such that
![]() $\mathsf {CT}_{0} \vdash U$
, there is an axiomatization
$\mathsf {CT}_{0} \vdash U$
, there is an axiomatization
![]() $\delta $
of
$\delta $
of
![]() $ {\mathsf {PA}}$
which is proof-theoretically equivalent to the usual axiomatization of
$ {\mathsf {PA}}$
which is proof-theoretically equivalent to the usual axiomatization of
![]() ${\textsf {PA}}$
and which has the property that the arithmetical consequences of the (finitely axiomatized) theoryFootnote
3
${\textsf {PA}}$
and which has the property that the arithmetical consequences of the (finitely axiomatized) theoryFootnote
3
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + T[\delta ]$
coincides with the deductive closure of
${\textsf {CT}}^-[{\textsf {EA}}] + T[\delta ]$
coincides with the deductive closure of
![]() $U.$
(Note that Theorem 6 provides us with an ample supply of theories U that Theorem 42 is applicable to.)
$U.$
(Note that Theorem 6 provides us with an ample supply of theories U that Theorem 42 is applicable to.)
Our other main results are structural. In Section 3.2, we focus on the collection
![]() $\mathsf {Sch}_{{\textsf {PA}}}$
consisting of the scheme templates
$\mathsf {Sch}_{{\textsf {PA}}}$
consisting of the scheme templates
![]() $\tau $
such that
$\tau $
such that
![]() ${\textsf {PA}}$
is deductively equivalent to the scheme generated by
${\textsf {PA}}$
is deductively equivalent to the scheme generated by
![]() $\tau $
(see Definitions 7 and 22). For example, in Theorem 30 we show that from the point of view of relative interpretability, theories of the form
$\tau $
(see Definitions 7 and 22). For example, in Theorem 30 we show that from the point of view of relative interpretability, theories of the form
![]() ${\textsf {CT}}^-[{\textsf {EA}}]+T[\tau ]$
, where
${\textsf {CT}}^-[{\textsf {EA}}]+T[\tau ]$
, where
![]() $\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
and
$\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
and
![]() $T[\tau ]$
is the sentence asserting that every instance of
$T[\tau ]$
is the sentence asserting that every instance of
![]() $\tau $
is true, have no maximal element.Footnote
4
In the same section we also prove that the partially ordered set
$\tau $
is true, have no maximal element.Footnote
4
In the same section we also prove that the partially ordered set
![]() $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
is universal for countable partial orderings (in particular, it contains infinite antichains, and also contains a copy of the linearly ordered set
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
is universal for countable partial orderings (in particular, it contains infinite antichains, and also contains a copy of the linearly ordered set
![]() $\mathbb {Q}$
of the rationals), where the partial ordering
$\mathbb {Q}$
of the rationals), where the partial ordering
![]() $\leq _{{\textsf {CT}}^-}$
is defined by
$\leq _{{\textsf {CT}}^-}$
is defined by
In Section 4.2, we prove similar results about the partial ordering
![]() $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
, where
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
, where
![]() $\Delta $
is the collection of elementary presentations of
$\Delta $
is the collection of elementary presentations of
![]() ${\textsf {PA}}$
that are proof-theoretically equivalent to (the canonical axiomatization of)
${\textsf {PA}}$
that are proof-theoretically equivalent to (the canonical axiomatization of)
![]() ${\textsf {PA}}$
. In particular we show that there is an embedding
${\textsf {PA}}$
. In particular we show that there is an embedding
![]() ${{\textsf {CT}}_0}/{{\textsf {PA}}}\hookrightarrow \langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
, where
${{\textsf {CT}}_0}/{{\textsf {PA}}}\hookrightarrow \langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
, where
![]() ${{\textsf {CT}}_0}/{{\textsf {PA}}}$
is the end segment of the Lindenbaum algebra of
${{\textsf {CT}}_0}/{{\textsf {PA}}}$
is the end segment of the Lindenbaum algebra of
![]() ${\textsf {PA}}$
generated by the collection of arithmetical consequences of
${\textsf {PA}}$
generated by the collection of arithmetical consequences of
![]() ${\textsf {CT}}_0$
.
${\textsf {CT}}_0$
.
Finally, in Theorem 58 of the last section of the paper we give a precise description of the set
![]() $\sup {\textsf {PA}}$
consisting of arithmetical sentences that are provable in some theory of the form
$\sup {\textsf {PA}}$
consisting of arithmetical sentences that are provable in some theory of the form
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + T[\delta ]$
, where
${\textsf {CT}}^-[{\textsf {EA}}] + T[\delta ]$
, where
![]() $\delta (x)$
is an elementary formula (in the sense of Definition 2) that defines an axiomatization of
$\delta (x)$
is an elementary formula (in the sense of Definition 2) that defines an axiomatization of
![]() ${\textsf {PA}}$
in the standard model
${\textsf {PA}}$
in the standard model
![]() $\mathbb {N}$
of arithmetic.
$\mathbb {N}$
of arithmetic.
Our results are motivated by (1) seeking a better understanding of the contours of the Tarski Boundary; (2) exploring the extent to which the statement “PA is true” is determinate in the context of the basic compositional truth theory
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
, and (3) further investigating structural aspects of finite axiomatizations of infinite theories, a topic initiated in the work of Pakhomov and Visser [Reference Pakhomov and Visser22].
${\textsf {CT}}^-[{\textsf {EA}}]$
, and (3) further investigating structural aspects of finite axiomatizations of infinite theories, a topic initiated in the work of Pakhomov and Visser [Reference Pakhomov and Visser22].
2 Preliminaries
2.1
 $ {\mathsf {CT}}^-$
,
$ {\mathsf {CT}}^-$
,
 ${\textsf {CT}}_0$
, and the Tarski Boundary
${\textsf {CT}}_0$
, and the Tarski Boundary
Definition 1.
![]() ${\textsf {Peano Arithmetic (PA)}}$
is the theory formulated in the language
${\textsf {Peano Arithmetic (PA)}}$
is the theory formulated in the language
![]() $\{0, S, + , \times \}$
whose axioms consist of the axioms of Robinson’s Arithmetic
$\{0, S, + , \times \}$
whose axioms consist of the axioms of Robinson’s Arithmetic
![]() ${\textsf {Q}}$
together with the induction scheme. We will denote the standard model of arithmetic by
${\textsf {Q}}$
together with the induction scheme. We will denote the standard model of arithmetic by
![]() $\mathbb {N}$
and its universe of discourse by
$\mathbb {N}$
and its universe of discourse by
![]() $\omega $
.
$\omega $
.
Definition 2.
![]() ${\textsf {Elementary Arithmetic (EA)}}$
is the fragment
${\textsf {Elementary Arithmetic (EA)}}$
is the fragment
![]() $\mathsf {I}\Delta _0 + \mathsf {Exp}$
of
$\mathsf {I}\Delta _0 + \mathsf {Exp}$
of
![]() ${\textsf {PA}}$
, where
${\textsf {PA}}$
, where
![]() $\mathsf {I}\Delta _0$
is the induction scheme for
$\mathsf {I}\Delta _0$
is the induction scheme for
![]() $\Delta _0$
-formulae (i.e., formulae with only bounded quantifiers), and
$\Delta _0$
-formulae (i.e., formulae with only bounded quantifiers), and
![]() $\mathsf {Exp}$
asserts the totality of the function
$\mathsf {Exp}$
asserts the totality of the function
![]() $\mathsf {exp}(x)=2^x$
(it is well-known that the graph of
$\mathsf {exp}(x)=2^x$
(it is well-known that the graph of
![]() $\mathsf {exp}$
can be described by a
$\mathsf {exp}$
can be described by a
![]() $\Delta _0$
-formula). An elementary formula is an arithmetical formula whose quantifiers are bounded by terms built from the function symbols S,
$\Delta _0$
-formula). An elementary formula is an arithmetical formula whose quantifiers are bounded by terms built from the function symbols S,
![]() $+$
,
$+$
,
![]() $\times $
, and
$\times $
, and
![]() $\mathsf {exp}$
. The family of (Kalmár) elementary functions is a distinguished subfamily of the primitive recursive functions.Footnote
5
It is well-known that the provably recursive functions of
$\mathsf {exp}$
. The family of (Kalmár) elementary functions is a distinguished subfamily of the primitive recursive functions.Footnote
5
It is well-known that the provably recursive functions of
![]() ${\textsf {EA}}$
are precisely the elementary functions; and that a function f is elementary iff f is computable by a Turing machine with a multiexponential time bound.
${\textsf {EA}}$
are precisely the elementary functions; and that a function f is elementary iff f is computable by a Turing machine with a multiexponential time bound.
Definition 3. We say that
![]() ${\textsf {B}}$
is a base theory if
${\textsf {B}}$
is a base theory if
![]() ${\textsf {B}}$
is formulated in
${\textsf {B}}$
is formulated in
![]() $\mathcal {L_{\mathsf {PA}}}$
with
$\mathcal {L_{\mathsf {PA}}}$
with
![]() ${\textsf {B}} \supseteq {\textsf {EA}}$
. We use
${\textsf {B}} \supseteq {\textsf {EA}}$
. We use
![]() $\mathcal {L}_{T}$
to refer to the language obtained by adding a unary predicate T to
$\mathcal {L}_{T}$
to refer to the language obtained by adding a unary predicate T to
![]() $\mathcal {L_{\mathsf {PA}}}$
.
$\mathcal {L_{\mathsf {PA}}}$
.
![]() ${\textsf {CT}}^-[{\textsf {B}}]$
is the theory extending
${\textsf {CT}}^-[{\textsf {B}}]$
is the theory extending
![]() ${\textsf {B}}$
with the
${\textsf {B}}$
with the
![]() $\mathcal {L}_{T}$
-sentences
$\mathcal {L}_{T}$
-sentences
![]() ${\textsf {CT}}1$
through
${\textsf {CT}}1$
through
![]() ${\textsf {CT}}5$
below.
${\textsf {CT}}5$
below.
We follow the notational conventions from [Reference Enayat, Łełyk and Wcisło5]. In particular
![]() $x \in {\mathsf {ClTerm}}_{\mathcal {L}_{ {\mathsf {PA}}}}$
is the arithmetical formula that expresses “x is (the code of) a closed term of
$x \in {\mathsf {ClTerm}}_{\mathcal {L}_{ {\mathsf {PA}}}}$
is the arithmetical formula that expresses “x is (the code of) a closed term of
![]() $\mathcal {L_{\mathsf {PA}}}$
”;
$\mathcal {L_{\mathsf {PA}}}$
”;
![]() $x \in {\mathsf {ClTermSeq}}_{\mathcal {L}_{ {\mathsf {PA}}}}$
is the arithmetical formula that expresses “x is (the code of) a sequence of closed terms of
$x \in {\mathsf {ClTermSeq}}_{\mathcal {L}_{ {\mathsf {PA}}}}$
is the arithmetical formula that expresses “x is (the code of) a sequence of closed terms of
![]() $\mathcal {L_{\mathsf {PA}}}$
”;
$\mathcal {L_{\mathsf {PA}}}$
”;
![]() $x \in { {\mathsf { Form}}}_{\mathcal {L}_{ {\mathsf {PA}}}}$
is the arithmetical formula that expresses “x is (the code of) a formula of
$x \in { {\mathsf { Form}}}_{\mathcal {L}_{ {\mathsf {PA}}}}$
is the arithmetical formula that expresses “x is (the code of) a formula of
![]() $\mathcal {L_{\mathsf {PA}}}$
”;
$\mathcal {L_{\mathsf {PA}}}$
”;
![]() $x \in { \mathsf {Sent}}_{\mathcal {L}_{ {\mathsf {PA}}}}$
is the arithmetical formula that expresses “x is (the code of) a sentence of
$x \in { \mathsf {Sent}}_{\mathcal {L}_{ {\mathsf {PA}}}}$
is the arithmetical formula that expresses “x is (the code of) a sentence of
![]() $\mathcal {L_{\mathsf {PA}}}$
”;
$\mathcal {L_{\mathsf {PA}}}$
”;
![]() $ x \in \mathsf {Var}$
expresses “x is (the code of) a variable”;
$ x \in \mathsf {Var}$
expresses “x is (the code of) a variable”;
![]() $ x \in \mathsf {VarSeq}$
expresses “x is (the code of) a sequence of variables”;
$ x \in \mathsf {VarSeq}$
expresses “x is (the code of) a sequence of variables”;
![]() $x \in { {\mathsf { Form}}}^{\leq n}_{\mathcal {L}_{ {\mathsf {PA}}}}$
expresses “x is a (the code of) formula of
$x \in { {\mathsf { Form}}}^{\leq n}_{\mathcal {L}_{ {\mathsf {PA}}}}$
expresses “x is a (the code of) formula of
![]() $\mathcal {L_{\mathsf {PA}}}$
with at most n distinct free variables”(n is not a variable in
$\mathcal {L_{\mathsf {PA}}}$
with at most n distinct free variables”(n is not a variable in
![]() ${\textsf {Form}}^{\leq n}_{\mathcal {L}_{{\textsf {PA}}}}$
);
${\textsf {Form}}^{\leq n}_{\mathcal {L}_{{\textsf {PA}}}}$
);
![]() $\underline {x}$
is (the code of) the numeral representing x;
$\underline {x}$
is (the code of) the numeral representing x;
![]() $\varphi [\underline {x}/v]$
is (the code of) the formula obtained by substituting the variable v with the numeral representing x and
$\varphi [\underline {x}/v]$
is (the code of) the formula obtained by substituting the variable v with the numeral representing x and
![]() $\varphi [\bar {s}/\bar {v}]$
has an analogous meaning for simultaneous substitution of terms from the sequence
$\varphi [\bar {s}/\bar {v}]$
has an analogous meaning for simultaneous substitution of terms from the sequence
![]() $\bar {s}$
for variables from the sequence
$\bar {s}$
for variables from the sequence
![]() $\bar {v}$
;
$\bar {v}$
;
![]() ${s}^{\circ }$
denotes the value of the term s, and
${s}^{\circ }$
denotes the value of the term s, and
![]() ${\bar {s}}^{\circ }$
denotes the sequence of numbers that correspond to values of terms from the sequence of terms
${\bar {s}}^{\circ }$
denotes the sequence of numbers that correspond to values of terms from the sequence of terms
![]() $\bar {s}$
.
$\bar {s}$
.
Finally, for better readability we will sometimes skip formulae denoting syntactic operations and write the effect of the operations instead. Thus, for example, we will write
![]() $T(\neg \varphi )$
to denote “There exists
$T(\neg \varphi )$
to denote “There exists
![]() $\psi $
which is the negation of the sentence
$\psi $
which is the negation of the sentence
![]() $\varphi $
and
$\varphi $
and
![]() $T(\psi ).$
”. For similar reasons, we shall often identify formulae with their Gödel codes. Where it is helpful to distinguish between the two,
$T(\psi ).$
”. For similar reasons, we shall often identify formulae with their Gödel codes. Where it is helpful to distinguish between the two,
![]() $\ulcorner \varphi \urcorner $
will denote the Gödel number of
$\ulcorner \varphi \urcorner $
will denote the Gödel number of
![]() $\varphi $
or the numeral naming this number (depending on the context).
$\varphi $
or the numeral naming this number (depending on the context).
-
 $ {\mathsf {CT}} 1$
$ {\mathsf {CT}} 1$
 $\forall s,t \in {\mathsf { ClTerm}}_{\mathcal {L}_{ {\mathsf {PA}}}} \ \ T(s=t)\leftrightarrow {s} ^{\circ } = {t}^{\circ }$
.
$\forall s,t \in {\mathsf { ClTerm}}_{\mathcal {L}_{ {\mathsf {PA}}}} \ \ T(s=t)\leftrightarrow {s} ^{\circ } = {t}^{\circ }$
. -
 $ {\mathsf {CT}} 2$
$ {\mathsf {CT}} 2$
 $\forall \varphi ,\psi \in { \mathsf {Sent}}_{\mathcal {L}_{ {\mathsf {PA}}}} \ \ T(\varphi \vee \psi )\leftrightarrow T(\varphi ) \vee T(\psi )$
.
$\forall \varphi ,\psi \in { \mathsf {Sent}}_{\mathcal {L}_{ {\mathsf {PA}}}} \ \ T(\varphi \vee \psi )\leftrightarrow T(\varphi ) \vee T(\psi )$
. -
 $ {\mathsf {CT}} 3$
$ {\mathsf {CT}} 3$
 $\forall \varphi \in {\mathsf { Sent}}_{\mathcal {L}_{ {\mathsf {PA}}}} \ \ T(\neg \varphi ) \leftrightarrow \neg T(\varphi )$
.
$\forall \varphi \in {\mathsf { Sent}}_{\mathcal {L}_{ {\mathsf {PA}}}} \ \ T(\neg \varphi ) \leftrightarrow \neg T(\varphi )$
. -
 $ {\mathsf {CT}} 4$
$ {\mathsf {CT}} 4$
 $\forall v\in \mathsf {Var}\forall \varphi \in { {\mathsf { Form}}}^{\leq 1}_{\mathcal {L}_{ {\mathsf {PA}}}} \ \ T(\exists v\varphi )\leftrightarrow \exists x~T(\varphi [\underline {x}/v])$
.
$\forall v\in \mathsf {Var}\forall \varphi \in { {\mathsf { Form}}}^{\leq 1}_{\mathcal {L}_{ {\mathsf {PA}}}} \ \ T(\exists v\varphi )\leftrightarrow \exists x~T(\varphi [\underline {x}/v])$
. -
 $ {\mathsf {CT}}5$
$ {\mathsf {CT}}5$
 $\forall \varphi (\bar {v})\in { \mathsf {Form}}_{\mathcal {L}_{ {\mathsf {PA}}}}\forall \bar {s},\bar {t} \in {\mathsf {ClTermSeq}}_{\mathcal {L}_{ {\mathsf {PA}}}}\ \ \big ( \bar {{s}^{\circ }}=\bar {{t}^{\circ }}\rightarrow T\left ( \varphi [ \bar {s}/\bar {v}]\right ) \leftrightarrow T \left ( \varphi [ \bar {t}/ \bar {v}]\right ) \big ).$
$\forall \varphi (\bar {v})\in { \mathsf {Form}}_{\mathcal {L}_{ {\mathsf {PA}}}}\forall \bar {s},\bar {t} \in {\mathsf {ClTermSeq}}_{\mathcal {L}_{ {\mathsf {PA}}}}\ \ \big ( \bar {{s}^{\circ }}=\bar {{t}^{\circ }}\rightarrow T\left ( \varphi [ \bar {s}/\bar {v}]\right ) \leftrightarrow T \left ( \varphi [ \bar {t}/ \bar {v}]\right ) \big ).$
The axiom
![]() ${\textsf {CT}}5$
is sometimes called generalized regularity, or generalized term-extensionality, and is not included in the accounts of
${\textsf {CT}}5$
is sometimes called generalized regularity, or generalized term-extensionality, and is not included in the accounts of
![]() ${\textsf {CT}}^-$
provided in the monographs of [Reference Cieśliński3, Reference Halbach10]. The conservativity of this particular version of
${\textsf {CT}}^-$
provided in the monographs of [Reference Cieśliński3, Reference Halbach10]. The conservativity of this particular version of
![]() $ {\mathsf {CT}}^{-}[ {\mathsf {PA}}]$
can be verified by a refinement of the model-theoretic method introduced in [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7], as presented both in [Reference Enayat, Łełyk and Wcisło5, Reference Kossak and Wcisło12]. Moreover, the following strengthening of the conservativity result in [Reference Enayat, Łełyk and Wcisło5].
$ {\mathsf {CT}}^{-}[ {\mathsf {PA}}]$
can be verified by a refinement of the model-theoretic method introduced in [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7], as presented both in [Reference Enayat, Łełyk and Wcisło5, Reference Kossak and Wcisło12]. Moreover, the following strengthening of the conservativity result in [Reference Enayat, Łełyk and Wcisło5].
Theorem 4. There is a polynomial-time computable function f such that for every
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
-proof
${\textsf {CT}}^-[{\textsf {PA}}]$
-proof
![]() $\pi $
of an arithmetical sentence
$\pi $
of an arithmetical sentence
![]() $\varphi $
,
$\varphi $
,
![]() $f(\pi )$
is a
$f(\pi )$
is a
![]() ${\textsf {PA}}$
-proof of
${\textsf {PA}}$
-proof of
![]() $\varphi $
. Moreover the correctness of f is verifiable in
$\varphi $
. Moreover the correctness of f is verifiable in
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
The above result shows that
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
is feasibly reducible to
${\textsf {CT}}^-[{\textsf {PA}}]$
is feasibly reducible to
![]() ${\textsf {PA}}$
. In particular, the basic truth theory
${\textsf {PA}}$
. In particular, the basic truth theory
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
admits at most a polynomial speed-up over
${\textsf {CT}}^-[{\textsf {PA}}]$
admits at most a polynomial speed-up over
![]() ${\textsf {PA}}$
. Moreover, as shown in [Reference Enayat, Łełyk and Wcisło5],
${\textsf {PA}}$
. Moreover, as shown in [Reference Enayat, Łełyk and Wcisło5],
![]() ${\textsf {PA}}$
proves the consistency of every finitely axiomatizable subtheory of
${\textsf {PA}}$
proves the consistency of every finitely axiomatizable subtheory of
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
, which together with the arithmetized completeness theorem and Orey’s compactness theorem shows that
${\textsf {CT}}^-[{\textsf {PA}}]$
, which together with the arithmetized completeness theorem and Orey’s compactness theorem shows that
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
is interpretable in
${\textsf {CT}}^-[{\textsf {PA}}]$
is interpretable in
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
Theorem 4 witnesses the “flatness” of
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
over its base theory
${\textsf {CT}}^-[{\textsf {PA}}]$
over its base theory
![]() ${\textsf {PA}}$
. The so-called Tarski Boundary project, seeks to map out the extent of this phenomenon. More concretely, given a metamathematical property of theories P which is exhibited by
${\textsf {PA}}$
. The so-called Tarski Boundary project, seeks to map out the extent of this phenomenon. More concretely, given a metamathematical property of theories P which is exhibited by
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
we are interested in determining which extensions of
${\textsf {CT}}^-[{\textsf {PA}}]$
we are interested in determining which extensions of
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
also exhibit P. In particular
${\textsf {CT}}^-[{\textsf {PA}}]$
also exhibit P. In particular
![]() $P(x)$
can stand for any of the properties below:
$P(x)$
can stand for any of the properties below:
-
• x is conservative over
 ${\textsf {PA}}$
.
${\textsf {PA}}$
. -
• x is relatively interpretable in
 ${\textsf {PA}}$
.
${\textsf {PA}}$
. -
• x admits at most a polynomial speed-up over
 ${\textsf {PA}}$
.
${\textsf {PA}}$
.
There is an obvious way of obtaining a natural strengthening of
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
which fails to have any of the above properties. To describe this strengthening, given a theory
${\textsf {CT}}^-[{\textsf {PA}}]$
which fails to have any of the above properties. To describe this strengthening, given a theory
![]() $\mathcal {T}$
let
$\mathcal {T}$
let
![]() ${\textsf {Pr}}_{\mathcal {T}}(\varphi )$
be the arithmetical formula that expresses “
${\textsf {Pr}}_{\mathcal {T}}(\varphi )$
be the arithmetical formula that expresses “
![]() $\varphi $
is provable from
$\varphi $
is provable from
![]() $\mathcal {T}$
,” where the axioms of
$\mathcal {T}$
,” where the axioms of
![]() $\mathcal {T}$
are given by some arithmetical formula. The Global Reflection for
$\mathcal {T}$
are given by some arithmetical formula. The Global Reflection for
![]() $\mathcal {T}$
is the following truth principle:
$\mathcal {T}$
is the following truth principle:
We stress that
![]() $\mathsf {GRP}(\mathcal {T})$
depends not only on
$\mathsf {GRP}(\mathcal {T})$
depends not only on
![]() $\mathcal {T}$
but also on the particularly chosen formula, which represents the axiom set of
$\mathcal {T}$
but also on the particularly chosen formula, which represents the axiom set of
![]() $\mathcal {T}$
. Below
$\mathcal {T}$
. Below
![]() ${\textsf {PA}}$
denotes the canonical formula which naturally represents the set of axioms of
${\textsf {PA}}$
denotes the canonical formula which naturally represents the set of axioms of
![]() ${\textsf {PA}}$
(as in Definition 1). Note that
${\textsf {PA}}$
(as in Definition 1). Note that
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
is non-conservative over
${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
is non-conservative over
![]() ${\textsf {PA}}$
since
${\textsf {PA}}$
since
![]() ${\textsf {Con}}_{{\textsf {PA}}}$
is provable in
${\textsf {Con}}_{{\textsf {PA}}}$
is provable in
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
. However,
${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
. However,
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
is much stronger, as indicated by the following result.
${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
is much stronger, as indicated by the following result.
Theorem 5 (Kotlarski [Reference Kotlarski13]–Smoryński [Reference Smoryński29], Łełyk [Reference Łełyk16]).
The arithmetical consequences of
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
coincides with
${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
coincides with
![]() $\mathsf {REF}^{<\omega }({\textsf {PA}})$
.
$\mathsf {REF}^{<\omega }({\textsf {PA}})$
.
In the above
![]() $\mathsf {REF}^0(\mathcal {T}):= \mathcal {T}$
,
$\mathsf {REF}^0(\mathcal {T}):= \mathcal {T}$
,
![]() $\mathsf {REF}^{n+1}(\mathcal {T}) := \mathsf {REF}(\mathsf {REF}^n(\mathcal {T}))$
,
$\mathsf {REF}^{n+1}(\mathcal {T}) := \mathsf {REF}(\mathsf {REF}^n(\mathcal {T}))$
,
![]() $\mathsf {REF}^{<\omega }(\mathcal {T}):= \bigcup _{n\in \omega }\mathsf {REF}^n(\mathcal {T})$
, where
$\mathsf {REF}^{<\omega }(\mathcal {T}):= \bigcup _{n\in \omega }\mathsf {REF}^n(\mathcal {T})$
, where
![]() $\mathsf {REF}(\mathcal {T})$
denotes the extension of
$\mathsf {REF}(\mathcal {T})$
denotes the extension of
![]() $\mathcal {T}$
with all instances of the Uniform Reflection Scheme for
$\mathcal {T}$
with all instances of the Uniform Reflection Scheme for
![]() $\mathcal {T}$
, i.e.,
$\mathcal {T}$
, i.e.,
![]() $\mathsf {REF}(\mathcal {T})$
consists of all sentences of the following form, where
$\mathsf {REF}(\mathcal {T})$
consists of all sentences of the following form, where
![]() $\varphi $
ranges over
$\varphi $
ranges over
![]() $\mathcal {L}_{\mathcal {T}}$
-formulae with at most one free variable:
$\mathcal {L}_{\mathcal {T}}$
-formulae with at most one free variable:
Interestingly enough, over
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
,
${\textsf {CT}}^-[{\textsf {EA}}]$
,
![]() $\mathsf {GRP}({\textsf {PA}})$
lends itself to many different characterisations, some of which express very basic properties of the truth predicate.
$\mathsf {GRP}({\textsf {PA}})$
lends itself to many different characterisations, some of which express very basic properties of the truth predicate.
Theorem 6. Over
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
the following are all equivalent to
${\textsf {CT}}^-[{\textsf {EA}}]$
the following are all equivalent to
![]() $\mathsf {GRP}({\textsf {PA}})$
:
$\mathsf {GRP}({\textsf {PA}})$
:
-
1.
 $\Delta _0$
-induction scheme for
$\Delta _0$
-induction scheme for
 $\mathcal {L}_T$
(see [Reference Łełyk16, Reference Łełyk17]).
$\mathcal {L}_T$
(see [Reference Łełyk16, Reference Łełyk17]). -
2.
 $\mathsf {GRP}(\emptyset )$
, i.e.,
$\mathsf {GRP}(\emptyset )$
, i.e.,
 $\forall \varphi \bigl ({\textsf {Pr}}_{\emptyset }(\varphi )\rightarrow T(\varphi )\bigr )$
(see [Reference Cieśliński2])
$\forall \varphi \bigl ({\textsf {Pr}}_{\emptyset }(\varphi )\rightarrow T(\varphi )\bigr )$
(see [Reference Cieśliński2]) -
3.
 $\forall c \bigl ("c \text { codes a set of sentences}"\wedge T(\bigvee _{\varphi \in c}\varphi )\rightarrow \exists \varphi \in c~ T(\varphi )\bigr )$
(see [Reference Cieśliński, Łełyk and Wcisło4]).
$\forall c \bigl ("c \text { codes a set of sentences}"\wedge T(\bigvee _{\varphi \in c}\varphi )\rightarrow \exists \varphi \in c~ T(\varphi )\bigr )$
(see [Reference Cieśliński, Łełyk and Wcisło4]).
Theorem 6 reveals the surprising robustness of the theory
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
. Out of the three above principles, the third one looks especially modest, being only one direction of a straightforward generalisation (often dubbed disjunctive correctness) of the compositional axiom
${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
. Out of the three above principles, the third one looks especially modest, being only one direction of a straightforward generalisation (often dubbed disjunctive correctness) of the compositional axiom
![]() ${\textsf {CT}}2$
of
${\textsf {CT}}2$
of
![]() ${\textsf {CT}}^-$
for disjunctions.Footnote
6
${\textsf {CT}}^-$
for disjunctions.Footnote
6
This shows that conceptually
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
is closer to the Tarski Boundary than previously conceived. One of the achievements of the current research is the discovery of the remarkable fact that this “conceptually small” area is populated by very different natural theories of truth, each of which “merely” expresses that
${\textsf {CT}}^-[{\textsf {PA}}]$
is closer to the Tarski Boundary than previously conceived. One of the achievements of the current research is the discovery of the remarkable fact that this “conceptually small” area is populated by very different natural theories of truth, each of which “merely” expresses that
![]() ${\textsf {PA}}$
is true.
${\textsf {PA}}$
is true.
-
• Note that by part (1) of Theorem 6,
 ${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
is also axiomatizable by the theory
${\textsf {CT}}^-[{\textsf {EA}}] + \mathsf {GRP}({\textsf {PA}})$
is also axiomatizable by the theory
 ${\textsf {CT}}_0[{\textsf {EA}}]$
, which is obtained by augmenting
${\textsf {CT}}_0[{\textsf {EA}}]$
, which is obtained by augmenting
 ${\textsf {CT}}^-[{\textsf {EA}}]$
with
${\textsf {CT}}^-[{\textsf {EA}}]$
with
 $\Delta _0$
-induction scheme for
$\Delta _0$
-induction scheme for
 $\mathcal {L}_T$
. Since this theory plays a very important role in our paper, for the sake of convenience we omit the reference to the base theory in
$\mathcal {L}_T$
. Since this theory plays a very important role in our paper, for the sake of convenience we omit the reference to the base theory in
 ${\textsf {CT}}_0[{\textsf {EA}}]$
and refer to it as
${\textsf {CT}}_0[{\textsf {EA}}]$
and refer to it as
 ${\textsf {CT}}_0$
. This is additionally justified by the fact that
${\textsf {CT}}_0$
. This is additionally justified by the fact that
 ${\textsf {CT}}_0[{\textsf {EA}}] = {\textsf {CT}}_0[{\textsf {B}}]$
for any base theory
${\textsf {CT}}_0[{\textsf {EA}}] = {\textsf {CT}}_0[{\textsf {B}}]$
for any base theory
 ${\textsf {B}}$
(i.e., any subtheory of
${\textsf {B}}$
(i.e., any subtheory of
 ${\textsf {PA}}$
that extends
${\textsf {PA}}$
that extends
 ${\textsf {EA}}$
).
${\textsf {EA}}$
).
As mentioned already in Section 1, our main focus in the current paper is on finite extensions of
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
that expresses “
${\textsf {CT}}^-[{\textsf {EA}}]$
that expresses “
![]() ${\textsf {PA}}$
is true.” As shown in Theorem 58, if we admit all elementary presentations of
${\textsf {PA}}$
is true.” As shown in Theorem 58, if we admit all elementary presentations of
![]() ${\textsf {PA}}$
, then each true
${\textsf {PA}}$
, then each true
![]() $\Pi _2$
-statement can be proved in a theory of this form. Hence, it is natural to look for some intuitive restrictions on “admissible” presentations of
$\Pi _2$
-statement can be proved in a theory of this form. Hence, it is natural to look for some intuitive restrictions on “admissible” presentations of
![]() ${\textsf {PA}}$
. We investigate two such admissible families of axiomatizations: schematic axiomatizations (introduced in Section 2.2) and prudent axiomatizations (introduced in Section 2.3). The former family is well-known; the latter family is defined in this paper as consisting of axiomatizations whose deductive equivalence to
${\textsf {PA}}$
. We investigate two such admissible families of axiomatizations: schematic axiomatizations (introduced in Section 2.2) and prudent axiomatizations (introduced in Section 2.3). The former family is well-known; the latter family is defined in this paper as consisting of axiomatizations whose deductive equivalence to
![]() ${\textsf {PA}}$
is verifiable in the weak, finitistically justified metatheory Primitive Recursive Arithemtic (
${\textsf {PA}}$
is verifiable in the weak, finitistically justified metatheory Primitive Recursive Arithemtic (
![]() $\mathsf {PRA}$
).
$\mathsf {PRA}$
).
2.2 Schematic axiomatizations
Definition 7. A template (for a scheme) is given by a sentence
![]() $\tau [P]$
formulated in the language obtained by augmenting
$\tau [P]$
formulated in the language obtained by augmenting
![]() $\mathcal {L}_{{\textsf {PA}}}$
with a predicate P, where P is unary.Footnote
7
An
$\mathcal {L}_{{\textsf {PA}}}$
with a predicate P, where P is unary.Footnote
7
An
![]() $\mathcal {L}_{{\textsf {PA}}}$
-sentence
$\mathcal {L}_{{\textsf {PA}}}$
-sentence
![]() $\psi $
is said to be an instance of
$\psi $
is said to be an instance of
![]() $\tau $
if
$\tau $
if
![]() $\psi $
is of the form
$\psi $
is of the form
![]() $\forall v~\tau [\varphi (x,v)/P]$
, where
$\forall v~\tau [\varphi (x,v)/P]$
, where
![]() $\tau [\varphi (x,v)/P]$
is the result of substituting all subformulae of the form
$\tau [\varphi (x,v)/P]$
is the result of substituting all subformulae of the form
![]() $P(t)$
, where t is a term, with
$P(t)$
, where t is a term, with
![]() $\varphi (t,v)$
(and re-naming bound variables of
$\varphi (t,v)$
(and re-naming bound variables of
![]() $\varphi $
to avoid unintended clashes). We use
$\varphi $
to avoid unintended clashes). We use
![]() $S_{\tau }$
to denote the collection of all instances of
$S_{\tau }$
to denote the collection of all instances of
![]() $\tau $
, and we refer to
$\tau $
, and we refer to
![]() $S_{\tau }$
as the scheme generated by
$S_{\tau }$
as the scheme generated by
![]() $\tau $
.
$\tau $
.
-
• We will use
 $T[\tau ]$
to refer to the
$T[\tau ]$
to refer to the
 $\mathcal {L}_{T}$
-sentence that says that each instance of
$\mathcal {L}_{T}$
-sentence that says that each instance of
 $S_{\tau }$
is true; more formally: In the above, the quantification
$S_{\tau }$
is true; more formally: In the above, the quantification $$ \begin{align*}T[\tau] := \forall v,w\in\mathsf{Var}~\forall \varphi(v,w) \in {\textsf{Form}}^{\leq 2}_{\mathcal{L}_{{\textsf{PA}}}}\ \forall z \ T(\tau[\varphi (v,\underline{z}/w)/P]).\end{align*} $$
$$ \begin{align*}T[\tau] := \forall v,w\in\mathsf{Var}~\forall \varphi(v,w) \in {\textsf{Form}}^{\leq 2}_{\mathcal{L}_{{\textsf{PA}}}}\ \forall z \ T(\tau[\varphi (v,\underline{z}/w)/P]).\end{align*} $$
 $\forall \varphi (v,w)\in {\textsf {Form}}^{\leq 2}_{\mathcal {L}_{{\textsf {PA}}}}$
expresses “for all formulae with at most two free variables
$\forall \varphi (v,w)\in {\textsf {Form}}^{\leq 2}_{\mathcal {L}_{{\textsf {PA}}}}$
expresses “for all formulae with at most two free variables
 $v,w$
.” (
$v,w$
.” (
 $\forall \varphi (v)\in {\textsf {Form}}^{\leq 1}_{\mathcal {L}_{{\textsf {PA}}}}$
below has an analogous meaning.) We note that, over
$\forall \varphi (v)\in {\textsf {Form}}^{\leq 1}_{\mathcal {L}_{{\textsf {PA}}}}$
below has an analogous meaning.) We note that, over
 ${\textsf {CT}}^-[{\textsf {EA}}]$
,
${\textsf {CT}}^-[{\textsf {EA}}]$
,
 $T[\tau ]$
is equivalent to the assertion We sometimes write “T is
$T[\tau ]$
is equivalent to the assertion We sometimes write “T is $$\begin{align*}\forall v\in\mathsf{Var}~\forall \varphi(v)\in{\textsf{Form}}^{\leq 1}_{\mathcal{L}_{{\textsf{PA}}}}~ T(\tau[\varphi(v)/P]).\end{align*}$$
$$\begin{align*}\forall v\in\mathsf{Var}~\forall \varphi(v)\in{\textsf{Form}}^{\leq 1}_{\mathcal{L}_{{\textsf{PA}}}}~ T(\tau[\varphi(v)/P]).\end{align*}$$
 $\tau $
-correct” instead of
$\tau $
-correct” instead of
 $T[\tau ]$
.
$T[\tau ]$
.
As mentioned in Section 1, the special case of the following theorem was established for
![]() ${\textsf {B}} = {\textsf {PA}}$
by Kotlarski, Krajewski, and Lachlan [Reference Kotlarski, Krajewski and Lachlan14], and in full generality by Enayat and Visser [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7], and Leigh [Reference Leigh15].
${\textsf {B}} = {\textsf {PA}}$
by Kotlarski, Krajewski, and Lachlan [Reference Kotlarski, Krajewski and Lachlan14], and in full generality by Enayat and Visser [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7], and Leigh [Reference Leigh15].
Theorem 8.
![]() $\mathsf {CT}^{-}\mathsf {[B]} +T[\tau ]$
is conservative over
$\mathsf {CT}^{-}\mathsf {[B]} +T[\tau ]$
is conservative over
![]() $\mathsf {B}$
for every base theory
$\mathsf {B}$
for every base theory
![]() ${\textsf {B}}$
and every scheme template
${\textsf {B}}$
and every scheme template
![]() $\tau $
such that
$\tau $
such that
![]() ${\textsf {B}}\vdash S_{\tau }$
.
${\textsf {B}}\vdash S_{\tau }$
.
We will need the following definition and classical result about partial truth definitions in the proof of Theorem 12 below.
Definition 9. The depth of a formula
![]() $\varphi $
is defined recursively by setting the depth of an arbitrary atomic formula to be zero, putting the depth of
$\varphi $
is defined recursively by setting the depth of an arbitrary atomic formula to be zero, putting the depth of
![]() $\neg \varphi $
and
$\neg \varphi $
and
![]() $\forall x \varphi $
to be one plus the depth of
$\forall x \varphi $
to be one plus the depth of
![]() $\varphi $
, the depth of
$\varphi $
, the depth of
![]() $\varphi \vee \psi $
to be one plus the maximum of depths of
$\varphi \vee \psi $
to be one plus the maximum of depths of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
. The depth of a term is defined similarly: the depth of a variable or a constant is zero and the depth of
$\psi $
. The depth of a term is defined similarly: the depth of a variable or a constant is zero and the depth of
![]() $t+s$
and
$t+s$
and
![]() $t\cdot s$
is one plus the maximum of depths of
$t\cdot s$
is one plus the maximum of depths of
![]() $t,s$
. The pure depth of the formula
$t,s$
. The pure depth of the formula
![]() $\varphi $
is the defined analogously to depth of
$\varphi $
is the defined analogously to depth of
![]() $\varphi $
, except for the condition for atomic formulae: the pure depth of a formula
$\varphi $
, except for the condition for atomic formulae: the pure depth of a formula
![]() $s=t$
is one plus the maximum of the depths of
$s=t$
is one plus the maximum of the depths of
![]() $s,t$
. The depth of a formula
$s,t$
. The depth of a formula
![]() $\varphi $
will be denoted with
$\varphi $
will be denoted with
![]() ${\textsf {depth}}(\varphi )$
, whereas its pure depth by
${\textsf {depth}}(\varphi )$
, whereas its pure depth by
![]() $\textsf {pdepth}(\varphi )$
. Observe that the depth of
$\textsf {pdepth}(\varphi )$
. Observe that the depth of
![]() $\varphi $
is always bounded above by its pure depth. We will write
$\varphi $
is always bounded above by its pure depth. We will write
where P is a unary predicate and y is a variable, for the formula obtained from the conjunction of
![]() ${\textsf {CT}} 1$
through
${\textsf {CT}} 1$
through
![]() ${\textsf {CT}} 4$
of Definition 3 in which (1) the predicate T is replaced by P, and (2) the universal quantifiers on
${\textsf {CT}} 4$
of Definition 3 in which (1) the predicate T is replaced by P, and (2) the universal quantifiers on
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are limited to formulae of depth at most y. Intuitively speaking,
$\psi $
are limited to formulae of depth at most y. Intuitively speaking,
![]() $\mathsf {True}(y,P)$
says that P satisfies the Tarskian compositional clauses for formulae of depth at most y.
$\mathsf {True}(y,P)$
says that P satisfies the Tarskian compositional clauses for formulae of depth at most y.
Example 10. The depth of an atomic formula is
![]() $0$
, whereas its pure depth can be arbitrarily large. The depth of
$0$
, whereas its pure depth can be arbitrarily large. The depth of
![]() $\exists x \bigl (x=S(S(0))\vee \neg x= x\bigr )$
is
$\exists x \bigl (x=S(S(0))\vee \neg x= x\bigr )$
is
![]() $3$
, whereas its pure depth is
$3$
, whereas its pure depth is
![]() $6$
.
$6$
.
The following theorem is classical; see [Reference Hájek and Pudlák9] for a proof.
Theorem 11 (Partial Truth Definitions).
For each
![]() $n \in \omega $
there is a unary
$n \in \omega $
there is a unary
![]() $\mathcal {L}_{{\textsf {PA}}}$
-formula
$\mathcal {L}_{{\textsf {PA}}}$
-formula
![]() $\mathsf {True}_n(x)$
such that the formula obtained by replacing y with
$\mathsf {True}_n(x)$
such that the formula obtained by replacing y with
![]() $\underline {n}$
and P with
$\underline {n}$
and P with
![]() $\mathsf {True}_n(x)$
in the formula
$\mathsf {True}_n(x)$
in the formula
![]() $\mathsf {True}(y,P)$
is provable in
$\mathsf {True}(y,P)$
is provable in
![]() ${\textsf {EA}}$
.
${\textsf {EA}}$
.
Theorem 12 (Vaught [Reference Vaught31], Visser [Reference Visser32]).
Let
![]() $\mathcal {T}$
be an r.e. theory with enough codingFootnote
8
, and let
$\mathcal {T}$
be an r.e. theory with enough codingFootnote
8
, and let
![]() $\mathcal {L}_{\mathcal {T}}$
be the language of
$\mathcal {L}_{\mathcal {T}}$
be the language of
![]() $\mathcal {T}$
. There is a primitive recursive function f (indeed f is elementary) such that given any unary
$\mathcal {T}$
. There is a primitive recursive function f (indeed f is elementary) such that given any unary
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\sigma $
that defines a set of
$\sigma $
that defines a set of
![]() $\mathcal {L}_{\mathcal {T}}$
-sentences
$\mathcal {L}_{\mathcal {T}}$
-sentences
![]() $\Phi $
in
$\Phi $
in
![]() $\mathbb {N}$
,
$\mathbb {N}$
,
![]() $f(\sigma )$
is a scheme template such that the deductive closures of
$f(\sigma )$
is a scheme template such that the deductive closures of
![]() $\mathcal {T} + S_{f(\sigma )}$
and
$\mathcal {T} + S_{f(\sigma )}$
and
![]() $\mathcal {T} + \Phi $
coincide.
$\mathcal {T} + \Phi $
coincide.
Proof outline for
 $\mathcal {T} = {\textsf {EA}}$
$\mathcal {T} = {\textsf {EA}}$
Suppose
![]() $\sigma (x)$
is a
$\sigma (x)$
is a
![]() $\Sigma _1$
-formula that defines a set
$\Sigma _1$
-formula that defines a set
![]() $\Phi $
of sentences of
$\Phi $
of sentences of
![]() $\mathcal {L}_{{\textsf {PA}}}$
in the standard model of arithmetic. (By Craig’s trick,
$\mathcal {L}_{{\textsf {PA}}}$
in the standard model of arithmetic. (By Craig’s trick,
![]() $\sigma $
can be chosen to be an elementary formula, this does not play a role in this proof, but it will come handy in the proof of Proposition 21, which is based on this one.) Let
$\sigma $
can be chosen to be an elementary formula, this does not play a role in this proof, but it will come handy in the proof of Proposition 21, which is based on this one.) Let
![]() $\mathsf {True}(y,P)$
be as in Definition 9. The desired scheme template
$\mathsf {True}(y,P)$
be as in Definition 9. The desired scheme template
![]() $\tau $
is
$\tau $
is
We note that:
(1)
![]() ${\textsf {EA}}+S_{\tau } \vdash \Phi $
, because for each
${\textsf {EA}}+S_{\tau } \vdash \Phi $
, because for each
![]() $n\in \omega $
the truth predicate for formulae of depth at most n is definable by Theorem 11; and
$n\in \omega $
the truth predicate for formulae of depth at most n is definable by Theorem 11; and
(2)
![]() ${\textsf {EA}}+\Phi \vdash S_{\tau }$
. To see this, suppose to the contrary that some instance
${\textsf {EA}}+\Phi \vdash S_{\tau }$
. To see this, suppose to the contrary that some instance
![]() $\psi $
of
$\psi $
of
![]() $S_{\tau }$
is not provable in
$S_{\tau }$
is not provable in
![]() ${\textsf {EA}}+\Phi $
. Then by the completeness theorem of first order logic there is a model
${\textsf {EA}}+\Phi $
. Then by the completeness theorem of first order logic there is a model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() ${\textsf {EA}} + \Phi + \lnot \psi $
. Since by the definition of
${\textsf {EA}} + \Phi + \lnot \psi $
. Since by the definition of
![]() $S_{\tau }$
there is a formula
$S_{\tau }$
there is a formula
![]() $\varphi (x,v)$
such that
$\varphi (x,v)$
such that
![]() $\psi $
is a sentence of the form
$\psi $
is a sentence of the form
![]() $\forall v~\tau [\varphi (x,v)/P]$
, we have
$\forall v~\tau [\varphi (x,v)/P]$
, we have
Thus
![]() $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
![]() ${\textsf {EA}} +\Phi $
in which the sentence
${\textsf {EA}} +\Phi $
in which the sentence
![]() $ \exists v ~\lnot \tau [\varphi (x,v)/P])$
holds, i.e.,
$ \exists v ~\lnot \tau [\varphi (x,v)/P])$
holds, i.e.,
![]() $\mathcal {M}\models \exists v \exists y \theta (v,y),$
where
$\mathcal {M}\models \exists v \exists y \theta (v,y),$
where
Let a and b be elements in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathcal {M}\models \theta (a,b)$
. The key observation at this point is that b cannot be a standard element since
$\mathcal {M}\models \theta (a,b)$
. The key observation at this point is that b cannot be a standard element since
![]() $\mathcal {M}\models \Phi .$
(It is precisely at this step that the argument would have broken down if we had used depth instead instead of pure depth in our formulation of the scheme template
$\mathcal {M}\models \Phi .$
(It is precisely at this step that the argument would have broken down if we had used depth instead instead of pure depth in our formulation of the scheme template
![]() $\tau $
.) Together with the fact that
$\tau $
.) Together with the fact that
![]() $\mathcal {M}\models \mathsf {True}(b,\varphi (x,a)/P)$
, this implies that the formula
$\mathcal {M}\models \mathsf {True}(b,\varphi (x,a)/P)$
, this implies that the formula
![]() $\varphi (x,a)$
defines a subset of
$\varphi (x,a)$
defines a subset of
![]() $\mathcal {M}$
that satisfies Tarski’s compositional clauses for all standard formulae, thus contradicting Tarski’s undefinability of truth theorem.
$\mathcal {M}$
that satisfies Tarski’s compositional clauses for all standard formulae, thus contradicting Tarski’s undefinability of truth theorem.
Remark 13. The proof of the above theorem would not go through, if in the definition of
![]() $\tau $
,
$\tau $
,
![]() $\textsf {pdepth}$
was changed to
$\textsf {pdepth}$
was changed to
![]() ${\textsf {depth}}$
. Indeed, assume
${\textsf {depth}}$
. Indeed, assume
![]() $\tau $
is modified accordingly. It is enough to take
$\tau $
is modified accordingly. It is enough to take
![]() $\Phi := \left \{{\textsf {Con}}_{{\textsf {EA}}}(\underline {n}) \ \ | \ \ n\in \omega \right \}$
, where
$\Phi := \left \{{\textsf {Con}}_{{\textsf {EA}}}(\underline {n}) \ \ | \ \ n\in \omega \right \}$
, where
![]() ${\textsf {Con}}_{{\textsf {EA}}}(x)$
expresses “there is no proof of inconsistency of
${\textsf {Con}}_{{\textsf {EA}}}(x)$
expresses “there is no proof of inconsistency of
![]() $\mathsf {EA}$
whose code is below x.” Let
$\mathsf {EA}$
whose code is below x.” Let
![]() $\sigma $
be the natural elementary definition of
$\sigma $
be the natural elementary definition of
![]() $\Phi $
, i.e.,
$\Phi $
, i.e.,
Observe that each sentence in
![]() $\Phi $
has the same, standard depth, call it k. Assume that
$\Phi $
has the same, standard depth, call it k. Assume that
![]() $\theta $
is a truth predicate for formulae of depth k. Then the sentence
$\theta $
is a truth predicate for formulae of depth k. Then the sentence
clearly implies
![]() ${\textsf {Con}}_{{\textsf {EA}}}$
, hence
${\textsf {Con}}_{{\textsf {EA}}}$
, hence
![]() $S_{\tau }$
is, over
$S_{\tau }$
is, over
![]() ${\textsf {EA}}$
, properly stronger than
${\textsf {EA}}$
, properly stronger than
![]() $\Phi $
.
$\Phi $
.
The above is the main reason for introducing both depth and pure depth of a formula into the picture. On the one hand, the natural definition of partial truth predicates involves the notion of depth. On the other, we need pure depth to make the proof of Theorem 12 work. The crucial difference between the two notions of depth is that in an arbitrary model
![]() $\mathcal {M}\models {\textsf {EA}}$
and for an arbitrary standard number n, if
$\mathcal {M}\models {\textsf {EA}}$
and for an arbitrary standard number n, if
![]() $\mathcal {M}\models {\textsf {Sent}}_{\mathcal {L}_{{\textsf {PA}}}}(\varphi )\wedge \mathsf {pdepth}(\varphi )\leq n$
, then
$\mathcal {M}\models {\textsf {Sent}}_{\mathcal {L}_{{\textsf {PA}}}}(\varphi )\wedge \mathsf {pdepth}(\varphi )\leq n$
, then
![]() $\varphi $
is “almost” a standard sentence: there is a standard sentence
$\varphi $
is “almost” a standard sentence: there is a standard sentence
![]() $\psi $
of the same pure depth as
$\psi $
of the same pure depth as
![]() $\varphi $
(
$\varphi $
(
![]() $\psi $
differs with
$\psi $
differs with
![]() $\varphi $
only w.r.t. the indices of bounded variables) such that for every formula
$\varphi $
only w.r.t. the indices of bounded variables) such that for every formula
![]() $P(x)$
such that
$P(x)$
such that
![]() $\mathcal {M}\models \mathsf {True}(n,P(x))$
we have
$\mathcal {M}\models \mathsf {True}(n,P(x))$
we have
![]() $\mathcal {M}\models P(\varphi )\leftrightarrow P(\psi ).$
$\mathcal {M}\models P(\varphi )\leftrightarrow P(\psi ).$
Remark 14. Note that by coupling Theorem 12 with the KKL Theorem we can readily obtain the so called Kleene–Vaught Theorem for extensions of
![]() ${\textsf {EA}}$
that asserts that every r.e. extension of
${\textsf {EA}}$
that asserts that every r.e. extension of
![]() ${\textsf {EA}}$
can be finitely axiomatized in an extended language. For another line of reasoning, see the proof of Proposition 47.
${\textsf {EA}}$
can be finitely axiomatized in an extended language. For another line of reasoning, see the proof of Proposition 47.
Remark 15. Let
![]() $\mathsf {Con_{ZF}}$
be the arithmetical statement asserting the consistency of
$\mathsf {Con_{ZF}}$
be the arithmetical statement asserting the consistency of
![]() $\mathsf {ZF}$
, and for each
$\mathsf {ZF}$
, and for each
![]() $n\in \omega $
let
$n\in \omega $
let
![]() ${\textsf {Con}}_{\mathsf {ZF}}(\underline {n})$
be the restricted consistency statement for
${\textsf {Con}}_{\mathsf {ZF}}(\underline {n})$
be the restricted consistency statement for
![]() $\mathsf {ZF}$
(that expresses “there is no proof of inconsistency of
$\mathsf {ZF}$
(that expresses “there is no proof of inconsistency of
![]() $\mathsf {ZF}$
whose code is below n”). Consider the following extension
$\mathsf {ZF}$
whose code is below n”). Consider the following extension
![]() ${\textsf {PA}}^{+}$
of
${\textsf {PA}}^{+}$
of
![]() ${\textsf {PA}}$
:
${\textsf {PA}}$
:
Then provably in
![]() $\mathsf {ZF}$
:
$\mathsf {ZF}$
:
To see that the above holds, we reason in
![]() $\mathsf {ZF}$
. Suppose
$\mathsf {ZF}$
. Suppose
![]() ${\textsf {PA}}^{+}$
is conservative over
${\textsf {PA}}^{+}$
is conservative over
![]() ${\textsf {PA}}$
. Then for all
${\textsf {PA}}$
. Then for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() ${\textsf {PA}}$
proves
${\textsf {PA}}$
proves
![]() ${\textsf {Con}}_{\mathsf {ZF}}(\underline {n})$
. On the other hand,
${\textsf {Con}}_{\mathsf {ZF}}(\underline {n})$
. On the other hand,
![]() $\mathsf {ZF}$
“knows” that
$\mathsf {ZF}$
“knows” that
![]() ${\textsf {PA}}$
holds in the standard model of arithmetic, so for all
${\textsf {PA}}$
holds in the standard model of arithmetic, so for all
![]() $n\in \omega $
, n is really not a proof of inconsistency of
$n\in \omega $
, n is really not a proof of inconsistency of
![]() $\mathsf {ZF}$
, i.e.,
$\mathsf {ZF}$
, i.e.,
![]() $\mathsf {Con_{ZF}}$
holds. On the other hand, if
$\mathsf {Con_{ZF}}$
holds. On the other hand, if
![]() $\mathsf {Con_{ZF}}$
holds, then by
$\mathsf {Con_{ZF}}$
holds, then by
![]() $\Sigma _{1}$
-completeness of
$\Sigma _{1}$
-completeness of
![]() ${\textsf {PA}}$
,
${\textsf {PA}}$
,
![]() ${\textsf {PA}}^{+}$
is conservative over
${\textsf {PA}}^{+}$
is conservative over
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
Moreover, by invoking Theorem 12, there is a scheme whose instances are provable in
![]() ${\textsf {PA}}$
(assuming
${\textsf {PA}}$
(assuming
![]() $\mathsf {Con_{ZF}}$
), but
$\mathsf {Con_{ZF}}$
), but
![]() $\mathsf {ZF}$
cannot verify this. Moreover, coupled with Theorem 8, and using part(c) of Definition 22, this also shows that there is a scheme template
$\mathsf {ZF}$
cannot verify this. Moreover, coupled with Theorem 8, and using part(c) of Definition 22, this also shows that there is a scheme template
![]() $\tau $
such that
$\tau $
such that
2.3 Prudent axiomatizations
In Section 4 we will investigate another intuitive restriction on “admissible” axiomatizations of
![]() ${\textsf {PA}}$
, namely axiomatizations that are prudent in the sense that their correctness can be verified in a finitistic metatheory. To formalize this intuition we use the well-entrenched notion of proof-theoretic reducibility.
${\textsf {PA}}$
, namely axiomatizations that are prudent in the sense that their correctness can be verified in a finitistic metatheory. To formalize this intuition we use the well-entrenched notion of proof-theoretic reducibility.
Definition 16. Let
![]() $\delta $
,
$\delta $
,
![]() $\delta '$
range over elementary formulae with one free variable. We say that
$\delta '$
range over elementary formulae with one free variable. We say that
![]() $\delta $
is proof-theoretically reducible to
$\delta $
is proof-theoretically reducible to
![]() $\delta '$
(
$\delta '$
(
![]() $\delta \leq _{pt}\delta '$
) if
$\delta \leq _{pt}\delta '$
) if
In the above
![]() ${\textsf {Pr}}_{\delta }(x)$
is the canonical provability predicate that expresses “There is a proof of x in First-Order Logic using the sentences from the set of axioms described by
${\textsf {Pr}}_{\delta }(x)$
is the canonical provability predicate that expresses “There is a proof of x in First-Order Logic using the sentences from the set of axioms described by
![]() $\delta $
as additional assumptions.” We write
$\delta $
as additional assumptions.” We write
![]() $\delta _{{\textsf {PA}}}$
for the elementary formula representing the usual axiomatization of
$\delta _{{\textsf {PA}}}$
for the elementary formula representing the usual axiomatization of
![]() ${\textsf {PA}}$
(as in Definition 1), i.e.,
${\textsf {PA}}$
(as in Definition 1), i.e.,
![]() $\delta _{{\textsf {PA}}}(x)$
expresses: x is either (the code of) an axiom of
$\delta _{{\textsf {PA}}}(x)$
expresses: x is either (the code of) an axiom of
![]() ${\textsf {Q}}$
or (the code of) an instance of the induction scheme. We say that
${\textsf {Q}}$
or (the code of) an instance of the induction scheme. We say that
![]() $\delta $
is proof-theoretically equivalent to
$\delta $
is proof-theoretically equivalent to
![]() $\delta _{{\textsf {PA}}}$
(written as
$\delta _{{\textsf {PA}}}$
(written as
![]() $\delta \sim _{pt} \delta _{{\textsf {PA}}}$
) if
$\delta \sim _{pt} \delta _{{\textsf {PA}}}$
) if
It is a classical fact due to Parsons [Reference Parsons, Kino, Myhill and Vesley24, Reference Parsons25] that I
![]() $\Sigma _1$
and the system of Primitive Recursive Arithmetic, known as
$\Sigma _1$
and the system of Primitive Recursive Arithmetic, known as
![]() $\mathsf {PRA}$
, have the same
$\mathsf {PRA}$
, have the same
![]() $\Pi _2$
-consequences. In particular it follows that whenever
$\Pi _2$
-consequences. In particular it follows that whenever
![]() $\delta \sim _{p.t.} \delta '$
, then in fact
$\delta \sim _{p.t.} \delta '$
, then in fact
![]() $\delta $
and
$\delta $
and
![]() $\delta '$
are deductively equivalent provably in PRA. As a consequence there are primitive recursive proof transformations mapping proofs in
$\delta '$
are deductively equivalent provably in PRA. As a consequence there are primitive recursive proof transformations mapping proofs in
![]() $\delta $
to proofs with the same conclusions in
$\delta $
to proofs with the same conclusions in
![]() $\delta '$
and vice-versa.
$\delta '$
and vice-versa.
-
• For the purposes of the results obtained in this paper, we do not need the full power of the proof-theoretic equivalence of
 $\delta $
and
$\delta $
and
 $\delta '$
to be verifiable in I
$\delta '$
to be verifiable in I
 $\Sigma _1$
since a theory as weak as Buss’s
$\Sigma _1$
since a theory as weak as Buss’s
 $S^1_2$
would be sufficient. (Thus we can require that there are polynomial-time computable proof transformations mapping proofs in
$S^1_2$
would be sufficient. (Thus we can require that there are polynomial-time computable proof transformations mapping proofs in
 $\delta $
to proofs with the same conclusions in
$\delta $
to proofs with the same conclusions in
 $\delta '$
and vice-versa.) However, we decided to stick to the more well-known notion of proof-theoretic reducibility rather than feasible reducibility, especially since the former notion is philosophically well-motivated by Hilbert’s finitism, as argued forcefully by Tait [Reference Tait30].
$\delta '$
and vice-versa.) However, we decided to stick to the more well-known notion of proof-theoretic reducibility rather than feasible reducibility, especially since the former notion is philosophically well-motivated by Hilbert’s finitism, as argued forcefully by Tait [Reference Tait30]. -
• We focus primarily on elementary presentations, rather than on, possibly more natural, r.e. axiomatizations for two reasons. First of all, for most of our main results, the simpler the axiomatizations, the better. (The results concerning them, mostly, have the form “For every x there is a prudent axiomatization
 $\delta $
such that ….”) Secondly, from the philosophical perspective, the elementary formulae, being decidable in multi-exponential time and hence absolute between models of
$\delta $
such that ….”) Secondly, from the philosophical perspective, the elementary formulae, being decidable in multi-exponential time and hence absolute between models of
 ${\textsf {EA}}$
, guarantee (or at least come closer to guaranteeing) that the notion of an axiom of the given theory is determinate. From these perspectives, feasible axiomatizations, i.e., P-Time decidable, axiomatizations would be even better, but we leave the investigation of such axiomatizations for further research.
${\textsf {EA}}$
, guarantee (or at least come closer to guaranteeing) that the notion of an axiom of the given theory is determinate. From these perspectives, feasible axiomatizations, i.e., P-Time decidable, axiomatizations would be even better, but we leave the investigation of such axiomatizations for further research.
Definition 17. We use
![]() $\Delta ^{*}$
to denote the collection of unary elementary formulae
$\Delta ^{*}$
to denote the collection of unary elementary formulae
![]() $\delta (x)$
such that
$\delta (x)$
such that
![]() $\delta ^{\mathbb {N}}:=\{n\in \omega ~|~\mathbb {N} \models \delta (\underline {n}) \}$
codes an
$\delta ^{\mathbb {N}}:=\{n\in \omega ~|~\mathbb {N} \models \delta (\underline {n}) \}$
codes an
![]() $\mathcal {L}_{{\textsf {PA}}}$
-theory that is deductively equivalent to
$\mathcal {L}_{{\textsf {PA}}}$
-theory that is deductively equivalent to
![]() ${\textsf {PA}}$
. We sometimes refer to the members of
${\textsf {PA}}$
. We sometimes refer to the members of
![]() $\Delta ^*$
as elementary presentations of
$\Delta ^*$
as elementary presentations of
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
-
• Given any arithmetical formula
 $\varphi $
with exactly one free variable, where x is the unique free variable of
$\varphi $
with exactly one free variable, where x is the unique free variable of $$ \begin{align*}T[\varphi(x)]:=\forall x \bigl(\varphi(x)\rightarrow T(x)\bigr),\end{align*} $$
$$ \begin{align*}T[\varphi(x)]:=\forall x \bigl(\varphi(x)\rightarrow T(x)\bigr),\end{align*} $$
 $\varphi $
. So
$\varphi $
. So
 $T[\varphi ]$
is the
$T[\varphi ]$
is the
 $\mathcal {L}_T$
-sentence expressing that the theory described by
$\mathcal {L}_T$
-sentence expressing that the theory described by
 $\varphi $
is true. Moreover, we put
$\varphi $
is true. Moreover, we put 
-
• We use
 $\Delta $
to denote the subset of
$\Delta $
to denote the subset of
 $\Delta ^*$
consisting of formulae
$\Delta ^*$
consisting of formulae
 $\delta \in \Delta ^*$
such that
$\delta \in \Delta ^*$
such that
 $\delta $
is proof-theoretically equivalent to
$\delta $
is proof-theoretically equivalent to
 $\delta _{\textsf {PA}}$
. Thus
$\delta _{\textsf {PA}}$
. Thus
 $\Delta $
is the collection of (defining formulae of) prudent axiomatizations of
$\Delta $
is the collection of (defining formulae of) prudent axiomatizations of
 ${\textsf {PA}}$
. Occasionally we also need the extension of
${\textsf {PA}}$
. Occasionally we also need the extension of
 $\Delta $
, denoted
$\Delta $
, denoted
 $\Delta ^-$
, defined On
$\Delta ^-$
, defined On $$\begin{align*}\Delta^-:= \left\{\delta\in \Delta^* \ \ | \ \ \delta\leq_{pt}{\textsf{PA}} \right\}.\end{align*}$$
$$\begin{align*}\Delta^-:= \left\{\delta\in \Delta^* \ \ | \ \ \delta\leq_{pt}{\textsf{PA}} \right\}.\end{align*}$$
 $\Delta ^-$
and
$\Delta ^-$
and
 $\Delta $
we shall consider the relation
$\Delta $
we shall consider the relation
 $\leq _{{\textsf {CT}}^-}$
given by
$\leq _{{\textsf {CT}}^-}$
given by  $$\begin{align*}\delta\leq_{{\textsf{CT}}^-}\delta' \iff {\textsf{CT}}^-[{\textsf{EA}}]\vdash T[\delta]\rightarrow T[\delta'].\end{align*}$$
$$\begin{align*}\delta\leq_{{\textsf{CT}}^-}\delta' \iff {\textsf{CT}}^-[{\textsf{EA}}]\vdash T[\delta]\rightarrow T[\delta'].\end{align*}$$
Convention 18. Simplifying things a little bit, when talking about the structures
![]() $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
and
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
and
![]() $\langle \Delta ^-, \leq _{{\textsf {CT}}^-}\rangle $
, we shall assume that
$\langle \Delta ^-, \leq _{{\textsf {CT}}^-}\rangle $
, we shall assume that
![]() $\Delta $
is replaced by the quotient set
$\Delta $
is replaced by the quotient set
![]() ${\Delta }/{ \sim } $
, where
${\Delta }/{ \sim } $
, where
![]() $\sim $
is the least equivalence relation that makes
$\sim $
is the least equivalence relation that makes
![]() $\leq _{{\textsf {CT}}^-}$
antisymmetric, to wit:
$\leq _{{\textsf {CT}}^-}$
antisymmetric, to wit:
-
• Let us stress an important difference between
 ${\textsf {CT}}^-[{\textsf {PA}}]$
and
${\textsf {CT}}^-[{\textsf {PA}}]$
and
 : the latter but not the former includes the sentence “All induction axioms are true.” In particular, the latter is finitely axiomatizable, while the former is known to be reflexive and therefore not finitely axiomatizable.
: the latter but not the former includes the sentence “All induction axioms are true.” In particular, the latter is finitely axiomatizable, while the former is known to be reflexive and therefore not finitely axiomatizable. -
• Note that the meaning of
 $T[\cdots ]$
depends on whether the object within the brackets is a scheme template, in which case
$T[\cdots ]$
depends on whether the object within the brackets is a scheme template, in which case
 $T[\cdots ]$
is interpreted as in Definition 7, or an arithmetical formula, in which case
$T[\cdots ]$
is interpreted as in Definition 7, or an arithmetical formula, in which case
 $T[\cdots ]$
has the meaning given in Definition 17. We shall try to reserve the use of variables
$T[\cdots ]$
has the meaning given in Definition 17. We shall try to reserve the use of variables
 $\tau $
,
$\tau $
,
 $\sigma ,$
etc. in this context for schematic templates and
$\sigma ,$
etc. in this context for schematic templates and
 $\varphi $
,
$\varphi $
,
 $\psi $
,
$\psi $
,
 $\delta ,$
etc. for formulae.
$\delta ,$
etc. for formulae.
Proposition 19. Both
![]() $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
and
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
and
![]() $\langle \Delta ^-, \leq _{{\textsf {CT}}^-}\rangle $
are distributive lattices.
$\langle \Delta ^-, \leq _{{\textsf {CT}}^-}\rangle $
are distributive lattices.
Proof We only present the proof for the case of
![]() $\Delta $
as it is
$\Delta $
as it is
![]() $(1+\varepsilon )$
-times harder. For showing that both structures are distributive lattices, it is enough to show that given
$(1+\varepsilon )$
-times harder. For showing that both structures are distributive lattices, it is enough to show that given
![]() $\delta ,\delta ' \in \Delta $
, one can find elements
$\delta ,\delta ' \in \Delta $
, one can find elements
![]() $\delta \oplus \delta '$
and
$\delta \oplus \delta '$
and
![]() $\delta \otimes \delta '$
of
$\delta \otimes \delta '$
of
![]() $\Delta $
such that over
$\Delta $
such that over
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
we have
${\textsf {CT}}^-[{\textsf {PA}}]$
we have
Indeed, this is because the Lindenbaum algebra of
![]() ${\textsf {CT}}^-$
is a distributive lattice. It can be readily seen that if we define
${\textsf {CT}}^-$
is a distributive lattice. It can be readily seen that if we define
then
![]() $\delta \oplus \delta ' \in \Delta $
and (1) is satisfied. For
$\delta \oplus \delta ' \in \Delta $
and (1) is satisfied. For
![]() $(2)$
it is sufficient to define
$(2)$
it is sufficient to define
where
![]() $x=y\vee z$
expresses that x is a disjunction of y and z. To see that (2) holds and
$x=y\vee z$
expresses that x is a disjunction of y and z. To see that (2) holds and
![]() $\delta _{{\textsf {PA}}}\leq _{pt} \delta \otimes \delta '$
one simply applies reasoning by cases; the proof of
$\delta _{{\textsf {PA}}}\leq _{pt} \delta \otimes \delta '$
one simply applies reasoning by cases; the proof of
![]() $\delta \otimes \delta '\leq _{pt}\delta _{{\textsf {PA}}}$
is trivial.
$\delta \otimes \delta '\leq _{pt}\delta _{{\textsf {PA}}}$
is trivial.
Remark 20. If
![]() $\delta \in \Delta $
corresponds to a schematic axiomatization of
$\delta \in \Delta $
corresponds to a schematic axiomatization of
![]() ${\textsf {PA}}$
(i.e., for some template
${\textsf {PA}}$
(i.e., for some template
![]() $\tau [P]$
,
$\tau [P]$
,
![]() $\delta (x)$
says that x is the result of substituting P with some unary arithmetical formula), then
$\delta (x)$
says that x is the result of substituting P with some unary arithmetical formula), then
![]() is a conservative extension of
is a conservative extension of
![]() ${\textsf {PA}}$
by Theorem 26. In contrast, even for very natural
${\textsf {PA}}$
by Theorem 26. In contrast, even for very natural
![]() $\delta \in \Delta $
,
$\delta \in \Delta $
,
![]() may be a highly non-conservative extension of
may be a highly non-conservative extension of
![]() ${\textsf {PA}}$
. For example, consider
${\textsf {PA}}$
. For example, consider
By a classical theorem of Kreisel, the union of
![]() ${\textsf {EA}}$
and
${\textsf {EA}}$
and
![]() $\mathsf {REF}_{{\textsf {EA}}}$
is deductively equivalent to
$\mathsf {REF}_{{\textsf {EA}}}$
is deductively equivalent to
![]() ${\textsf {PA}}$
(see, e.g., [Reference Beklemishev1, p. 39]). Let
${\textsf {PA}}$
(see, e.g., [Reference Beklemishev1, p. 39]). Let
![]() $\delta (x)$
be a natural elementary definition of
$\delta (x)$
be a natural elementary definition of
![]() ${\textsf {EA}} \cup \mathsf {REF}_{{\textsf {EA}}}$
. Then, in fact
${\textsf {EA}} \cup \mathsf {REF}_{{\textsf {EA}}}$
. Then, in fact
![]() $\delta \in \Delta $
. An easy argument shows that
$\delta \in \Delta $
. An easy argument shows that
However, by a theorem of [Reference Cieśliński2], over
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
, the above consequence of
${\textsf {CT}}^-[{\textsf {EA}}]$
, the above consequence of
implies the Global Reflection Principle for
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
Proposition 21. Every
![]() $\mathcal {L}_{{\textsf {PA}}}$
-theory
$\mathcal {L}_{{\textsf {PA}}}$
-theory
![]() $\mathcal {T}$
extending
$\mathcal {T}$
extending
![]() ${\textsf {EA}}$
whose axioms are described by an elementary formula
${\textsf {EA}}$
whose axioms are described by an elementary formula
![]() $\delta $
(in the standard model of arithmetic) has a proof-theoretically equivalent presentation
$\delta $
(in the standard model of arithmetic) has a proof-theoretically equivalent presentation
![]() $\delta '$
such that
$\delta '$
such that
![]() is a conservative extension of
is a conservative extension of
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Proof Fix
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\delta $
as in the assumptions. Let
$\delta $
as in the assumptions. Let
![]() $\delta '$
be the natural elementary definition of the set
$\delta '$
be the natural elementary definition of the set
![]() $S_{\tau }$
, where
$S_{\tau }$
, where
![]() $\tau $
is the template defined as in the proof of Theorem 12. This works, since in the proof of Theorem 12, the verification of the fact that the deductive closure of
$\tau $
is the template defined as in the proof of Theorem 12. This works, since in the proof of Theorem 12, the verification of the fact that the deductive closure of
![]() ${\textsf {EA}}+ S_{\tau }$
and
${\textsf {EA}}+ S_{\tau }$
and
![]() ${\textsf {EA}} + \Phi $
coincide formalizes smoothly in the subsystem
${\textsf {EA}} + \Phi $
coincide formalizes smoothly in the subsystem
![]() $\mathsf {WKL^{*}_0}$
of second order arithmetic, which is well-known to be a conservative extension of
$\mathsf {WKL^{*}_0}$
of second order arithmetic, which is well-known to be a conservative extension of
![]() ${\textsf {EA}}$
, as first shown in [Reference Simpson and Smith28]. More explicitly, the verification of
${\textsf {EA}}$
, as first shown in [Reference Simpson and Smith28]. More explicitly, the verification of
![]() ${\textsf {EA}}+ S_{\tau }\vdash \Phi $
requires only the existence of well-behaved partial truth predicates (that can be developed within
${\textsf {EA}}+ S_{\tau }\vdash \Phi $
requires only the existence of well-behaved partial truth predicates (that can be developed within
![]() ${\textsf {EA}}$
, as demonstrated, e.g., in [Reference Beklemishev1, Proposition 2.6]). On the other hand, the verification of
${\textsf {EA}}$
, as demonstrated, e.g., in [Reference Beklemishev1, Proposition 2.6]). On the other hand, the verification of
![]() ${\textsf {EA}} + \Phi \vdash S_{\tau }$
requires the completeness theorem of first order logic (which is readily available in
${\textsf {EA}} + \Phi \vdash S_{\tau }$
requires the completeness theorem of first order logic (which is readily available in
![]() $\mathsf {WKL^{*}_0}$
) together with Tarski’s undefinability of truth theorem. Although Tarski’s theorem presupposes the consistency of
$\mathsf {WKL^{*}_0}$
) together with Tarski’s undefinability of truth theorem. Although Tarski’s theorem presupposes the consistency of
![]() $\Phi $
, this can be assumed, because if
$\Phi $
, this can be assumed, because if
![]() $\Phi $
is inconsistent, so is
$\Phi $
is inconsistent, so is
![]() $S_{\tau }$
by the proof of the first implication, and in such a scenario the two theories clearly coincide. Hence
$S_{\tau }$
by the proof of the first implication, and in such a scenario the two theories clearly coincide. Hence
![]() $\delta '$
is indeed proof-theoretically reducible to
$\delta '$
is indeed proof-theoretically reducible to
![]() $\delta $
. However, in this case
$\delta $
. However, in this case
![]() is trivially equivalent to
is trivially equivalent to
![]() ${\textsf {CT}}^-[{\textsf {PA}}] + T[\tau ]$
, hence is a conservative extension of
${\textsf {CT}}^-[{\textsf {PA}}] + T[\tau ]$
, hence is a conservative extension of
![]() $\mathcal {T}$
, due to Theorem 8.
$\mathcal {T}$
, due to Theorem 8.
3 Schematically correct axiomatizations
3.1 Complexity
Definition 22. In the following definitions
![]() $\tau $
ranges over scheme templates and
$\tau $
ranges over scheme templates and
![]() $S _{\tau }$
is the corresponding scheme (in the sense of Definition 7) generated by
$S _{\tau }$
is the corresponding scheme (in the sense of Definition 7) generated by
![]() $\tau $
.
$\tau $
.
-
(a)
 $\mathsf {Sch}_{\mathsf {PA}}^{-}:=\{\tau :\mathsf {PA}\vdash S _{\tau }\},$
i.e.,
$\mathsf {Sch}_{\mathsf {PA}}^{-}:=\{\tau :\mathsf {PA}\vdash S _{\tau }\},$
i.e.,
 $\mathsf {Sch}_{\mathsf {PA}}^{-}$
is the collection of templates whose corresponding scheme is
$\mathsf {Sch}_{\mathsf {PA}}^{-}$
is the collection of templates whose corresponding scheme is
 ${\textsf {PA}}$
-provable.
${\textsf {PA}}$
-provable. -
(b)
 $\mathsf {Sch}_{\mathsf {PA}}:=\{\tau \in \mathsf {Sch}_{ \mathsf {PA}}^{-}:S_{\tau }\vdash \mathsf {PA}\}$
, i.e.,
$\mathsf {Sch}_{\mathsf {PA}}:=\{\tau \in \mathsf {Sch}_{ \mathsf {PA}}^{-}:S_{\tau }\vdash \mathsf {PA}\}$
, i.e.,
 $\mathsf {Sch}_{ \mathsf {PA}}$
is the collection of templates whose corresponding scheme is an axiomatization of
$\mathsf {Sch}_{ \mathsf {PA}}$
is the collection of templates whose corresponding scheme is an axiomatization of
 ${\textsf {PA}}$
.
${\textsf {PA}}$
. -
(c)
 $\mathsf {Sch}_{{\textsf {PA}}}^{\mathsf {T}}$
is the collection of templates
$\mathsf {Sch}_{{\textsf {PA}}}^{\mathsf {T}}$
is the collection of templates
 $\tau $
such that the arithmetical consequences of
$\tau $
such that the arithmetical consequences of
 $\mathsf {CT}^{-}[{\textsf {EA}}]+T[\tau ]$
coincides with
$\mathsf {CT}^{-}[{\textsf {EA}}]+T[\tau ]$
coincides with
 ${\textsf {PA}}$
(recall that
${\textsf {PA}}$
(recall that
 $T[\tau ]$
says that T is
$T[\tau ]$
says that T is
 $\tau $
-correct, as in Definition 7).
$\tau $
-correct, as in Definition 7). -
(d)
 $\mathsf {Cons}:=\{\varphi \in \mathcal {L}_{T}: \mathsf {CT}^{-}[\mathsf {PA}]+\varphi $
is conservative over
$\mathsf {Cons}:=\{\varphi \in \mathcal {L}_{T}: \mathsf {CT}^{-}[\mathsf {PA}]+\varphi $
is conservative over
 ${\textsf {PA}}$
}.
${\textsf {PA}}$
}.
Recall that in Section 1 we defined
![]() $\leq _{{\textsf {CT}}^-}$
on
$\leq _{{\textsf {CT}}^-}$
on
![]() $\mathsf {Sch}^-_{{\textsf {PA}}}$
as follows:
$\mathsf {Sch}^-_{{\textsf {PA}}}$
as follows:
Note that at this point
![]() $\leq _{{\textsf {CT}}^-}$
denotes both the ordering on scheme templates and the ordering on prudent axiomatizations. As the notation “
$\leq _{{\textsf {CT}}^-}$
denotes both the ordering on scheme templates and the ordering on prudent axiomatizations. As the notation “
![]() $\leq _{{\textsf {CT}}^-}$
” will never be used in isolation this shouldn’t lead to serious confusion. When talking about the structural properties of
$\leq _{{\textsf {CT}}^-}$
” will never be used in isolation this shouldn’t lead to serious confusion. When talking about the structural properties of
![]() $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
we shall tacitly assume that
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
we shall tacitly assume that
![]() $\mathsf {Sch}_{{\textsf {PA}}}$
is factored out by an appropriate equivalence relation, so as to make
$\mathsf {Sch}_{{\textsf {PA}}}$
is factored out by an appropriate equivalence relation, so as to make
![]() $\leq _{{\textsf {CT}}^-}$
a partial order (as in Convention 18).
$\leq _{{\textsf {CT}}^-}$
a partial order (as in Convention 18).
Proposition 23.
![]() $\langle \mathsf {Sch}^-_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
$\langle \mathsf {Sch}^-_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
![]() $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
are distributive lattices.
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
are distributive lattices.
Proof As previously we do the case of a smaller structure, with
![]() $\mathsf {Sch}_{{\textsf {PA}}}$
as the universe. Arguing as previously in Proposition 19, it is enough to define
$\mathsf {Sch}_{{\textsf {PA}}}$
as the universe. Arguing as previously in Proposition 19, it is enough to define
![]() $\oplus $
and
$\oplus $
and
![]() $\otimes $
such that
$\otimes $
such that
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
proves the following for all
${\textsf {CT}}^-[{\textsf {PA}}]$
proves the following for all
![]() $\tau ,~\tau ' \in \mathsf {Sch}_{{\textsf {PA}}}$
:
$\tau ,~\tau ' \in \mathsf {Sch}_{{\textsf {PA}}}$
:
The case of
![]() $\oplus $
is trivial. We put
$\oplus $
is trivial. We put
The case of
![]() $\otimes $
is (a little bit) harder. We put
$\otimes $
is (a little bit) harder. We put
where Q is a fresh unary predicate. As remarked earlier (compare footnote 4) thanks to the coding apparatus,
![]() $\tau \otimes \tau '$
can be expressed as a scheme with a single unary predicate P. Then we obtain
$\tau \otimes \tau '$
can be expressed as a scheme with a single unary predicate P. Then we obtain
It is very easy now to check that
![]() $(4)$
is satisfied.
$(4)$
is satisfied.
We note that the above proof adapts to the case of
![]() $\langle \mathsf {Sch}^{\mathsf {T}}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
. Quite in the opposite direction, it can be shown that
$\langle \mathsf {Sch}^{\mathsf {T}}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
. Quite in the opposite direction, it can be shown that
![]() $\langle \mathsf {Cons}, \leq _{{\textsf {CT}}^-}\rangle $
is not even a lattice as there are two sentences
$\langle \mathsf {Cons}, \leq _{{\textsf {CT}}^-}\rangle $
is not even a lattice as there are two sentences
![]() $\varphi ,\psi \in \mathsf {Cons}$
such that
$\varphi ,\psi \in \mathsf {Cons}$
such that
![]() ${\textsf {CT}}^[{\textsf {PA}}] + \varphi +\psi $
is a non-conservative extension of
${\textsf {CT}}^[{\textsf {PA}}] + \varphi +\psi $
is a non-conservative extension of
![]() ${\textsf {PA}}$
. First examples of such sentences were discovered by Bartosz Wcisło (unpublished). We plan to present a family of such examples in the forthcoming sequel [Reference Łełyk18] to the current paper.
${\textsf {PA}}$
. First examples of such sentences were discovered by Bartosz Wcisło (unpublished). We plan to present a family of such examples in the forthcoming sequel [Reference Łełyk18] to the current paper.
Theorem 24 (KKL-Theorem, first formulation).
![]() ${\textsf {CT}}^{-}[{\textsf {PA}}]+ T[\tau ]$
is conservative over
${\textsf {CT}}^{-}[{\textsf {PA}}]+ T[\tau ]$
is conservative over
![]() $\mathsf {PA}$
for each
$\mathsf {PA}$
for each
![]() $\tau \in \mathsf {Sch}_{{\textsf {PA}}}^{-}$
.
$\tau \in \mathsf {Sch}_{{\textsf {PA}}}^{-}$
.
Let
![]() $\Theta $
be the union of sentences of the form
$\Theta $
be the union of sentences of the form
![]() $T[\tau ]$
(expressing that T is
$T[\tau ]$
(expressing that T is
![]() $\tau $
-correct) as
$\tau $
-correct) as
![]() $\tau $
ranges in
$\tau $
ranges in
![]() $\mathsf {Sch}_{\mathsf {PA}}^{-}$
. Since the union of two schemes is axiomatizable by a single scheme, the KKL-theorem can be reformulated as:
$\mathsf {Sch}_{\mathsf {PA}}^{-}$
. Since the union of two schemes is axiomatizable by a single scheme, the KKL-theorem can be reformulated as:
Theorem 25 (KKL-Theorem, second formulation).
![]() ${\textsf {CT}}^{-}[{\textsf {PA}}] +\Theta $
is conservative over
${\textsf {CT}}^{-}[{\textsf {PA}}] +\Theta $
is conservative over
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
The above formulation naturally suggests the question: How complicated is
![]() $\Theta $
(viewed as a subset of
$\Theta $
(viewed as a subset of
![]() $\omega $
)? Is it recursively enumerable? The result below shows that
$\omega $
)? Is it recursively enumerable? The result below shows that
![]() $\Theta $
is
$\Theta $
is
![]() $\Pi _{2}$
-complete, since
$\Pi _{2}$
-complete, since
![]() $\Theta $
is readily seen to be recursively isomorphic to
$\Theta $
is readily seen to be recursively isomorphic to
![]() $\mathsf {Sch}_{\mathsf {PA}}^{-}$
(indeed the isomorphism is witnessed by an elementary function). Therefore,
$\mathsf {Sch}_{\mathsf {PA}}^{-}$
(indeed the isomorphism is witnessed by an elementary function). Therefore,
![]() $\Theta $
is pretty far from being recursively enumerable.
$\Theta $
is pretty far from being recursively enumerable.
Theorem 26. The sets
![]() $\mathsf {Sch}_{\mathsf {PA}}^{-}$
,
$\mathsf {Sch}_{\mathsf {PA}}^{-}$
,
![]() $\mathsf {Sch}_{ \mathsf {PA}}$
,
$\mathsf {Sch}_{ \mathsf {PA}}$
,
![]() $\mathsf {Sch}_{\mathsf {PA}}^{\mathsf {T}}$
, and
$\mathsf {Sch}_{\mathsf {PA}}^{\mathsf {T}}$
, and
![]() $\mathsf {Cons}$
are all
$\mathsf {Cons}$
are all
![]() $\Pi _{2}$
-complete.
$\Pi _{2}$
-complete.
Proof Each of the four sets is readily seen to be definable by a
![]() $\Pi _{2}$
-formula, so it suffices to show that each is
$\Pi _{2}$
-formula, so it suffices to show that each is
![]() $\Pi _{2}$
-hard, i.e., the complete
$\Pi _{2}$
-hard, i.e., the complete
![]() $\Pi _{2}$
-set
$\Pi _{2}$
-set
![]() $\mathsf {True}_{\Pi _{2}}^{\mathbb {N}}$
consisting of (Gödel numbers of)
$\mathsf {True}_{\Pi _{2}}^{\mathbb {N}}$
consisting of (Gödel numbers of)
![]() $\Pi _{2}$
-sentences that are true in the standard model
$\Pi _{2}$
-sentences that are true in the standard model
![]() $\mathbb {N}$
of
$\mathbb {N}$
of
![]() ${\textsf {PA}}$
is many-one reducible (denoted
${\textsf {PA}}$
is many-one reducible (denoted
![]() $\leq _{\mathsf {m}} $
) to each of them. Recall that
$\leq _{\mathsf {m}} $
) to each of them. Recall that
![]() $\leq _{\mathsf {m}} $
is defined among subsets of
$\leq _{\mathsf {m}} $
is defined among subsets of
![]() $\omega $
via:
$\omega $
via:
The proof will be complete once we demonstrate the following four assertions:
-
(i)
 $\mathsf {True}_{\Pi _{2}}^{\mathbb {N}}\leq _{\mathsf {m}} \mathsf {Sch}_{{\textsf {PA}}}^{-}$
.Footnote
9
$\mathsf {True}_{\Pi _{2}}^{\mathbb {N}}\leq _{\mathsf {m}} \mathsf {Sch}_{{\textsf {PA}}}^{-}$
.Footnote
9
-
(ii)
 $\mathsf {Sch}_{\mathsf {PA}}^{-}\leq _{\mathsf {m}} \mathsf {Sch}_{\mathsf {PA}}.$
$\mathsf {Sch}_{\mathsf {PA}}^{-}\leq _{\mathsf {m}} \mathsf {Sch}_{\mathsf {PA}}.$
-
(iii)
 $\mathsf {Sch}_{\mathsf {PA}}^{-}\leq _{\mathsf {m}} \ \mathsf {Sch}_{ \mathsf {PA}}^{T}.$
$\mathsf {Sch}_{\mathsf {PA}}^{-}\leq _{\mathsf {m}} \ \mathsf {Sch}_{ \mathsf {PA}}^{T}.$
-
(iv)
 $\mathsf {True}_{\Pi _{2}}^{\mathbb {N}}\leq _{\mathsf {m}} \mathsf {Cons}$
.
$\mathsf {True}_{\Pi _{2}}^{\mathbb {N}}\leq _{\mathsf {m}} \mathsf {Cons}$
.
To prove
![]() $(i)$
, suppose
$(i)$
, suppose
![]() $\pi =\forall x\ \exists y\ \delta (x,y)$
is a
$\pi =\forall x\ \exists y\ \delta (x,y)$
is a
![]() $\Pi _{2}$
-statement, where
$\Pi _{2}$
-statement, where
![]() $\delta (x,y)$
is
$\delta (x,y)$
is
![]() $\Delta _{0}$
. We first observe that by
$\Delta _{0}$
. We first observe that by
![]() $\Sigma _{1}$
-completeness of
$\Sigma _{1}$
-completeness of
![]() ${\textsf {PA}}$
:
${\textsf {PA}}$
:
![]() $(\ast ) \ \pi \in \mathrm {True}_{\Pi _{2}}^{\mathbb {N}}$
iff
$(\ast ) \ \pi \in \mathrm {True}_{\Pi _{2}}^{\mathbb {N}}$
iff
![]() $ \forall n\in \omega \ \mathrm {PA}\vdash \exists y\ \delta (\underline {n},y)$
.
$ \forall n\in \omega \ \mathrm {PA}\vdash \exists y\ \delta (\underline {n},y)$
.
On the other hand,
![]() $R=\{\exists y\ \delta (\underline {n},y):n\in \omega \}$
is a recursive set of sentences, so by Theorem 12 there is
$R=\{\exists y\ \delta (\underline {n},y):n\in \omega \}$
is a recursive set of sentences, so by Theorem 12 there is
![]() $\tau $
such that
$\tau $
such that
![]() $\tau \in \mathsf {Sch}_{\mathsf {PA}}^{-}$
iff
$\tau \in \mathsf {Sch}_{\mathsf {PA}}^{-}$
iff
![]() $\mathsf {PA} \vdash R.$
To finish the proof, it remains to observe that the transition from
$\mathsf {PA} \vdash R.$
To finish the proof, it remains to observe that the transition from
![]() $\pi $
to the
$\pi $
to the
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\sigma $
that defines R in
$\sigma $
that defines R in
![]() $\mathbb {N}$
is given by a recursive function g, therefore if f is the total recursive function as in Theorem 12 then we have
$\mathbb {N}$
is given by a recursive function g, therefore if f is the total recursive function as in Theorem 12 then we have
The proof of
![]() $(ii)$
is based on the observation that
$(ii)$
is based on the observation that
![]() $\tau \in \mathsf {Sch}^{-} _{\mathsf {PA}}$
iff
$\tau \in \mathsf {Sch}^{-} _{\mathsf {PA}}$
iff
![]() $h(\tau )\in \mathsf {Sch}_{\mathsf {PA}}$
, where
$h(\tau )\in \mathsf {Sch}_{\mathsf {PA}}$
, where
![]() $h(\tau ):=\tau \wedge \tau _{\mathsf {PA}}$
, and
$h(\tau ):=\tau \wedge \tau _{\mathsf {PA}}$
, and
![]() $\tau _{{\textsf {PA}}}$
is defined as follows:
$\tau _{{\textsf {PA}}}$
is defined as follows:
To verify
![]() $(iii)$
, we claim that
$(iii)$
, we claim that
![]() $\tau \in \mathsf { Sch}_{\mathsf {PA}}^{-}$
iff
$\tau \in \mathsf { Sch}_{\mathsf {PA}}^{-}$
iff
![]() $\left ( \tau \wedge \tau _{\mathsf {PA} }\right ) \in \mathsf {Sch}_{\mathsf {PA}}^{T}$
. The implication
$\left ( \tau \wedge \tau _{\mathsf {PA} }\right ) \in \mathsf {Sch}_{\mathsf {PA}}^{T}$
. The implication
![]() $ \tau \in \mathsf {Sch}_{\mathsf {PA}}^{-}\Rightarrow \left ( \tau \wedge \tau _{\mathsf {PA}}\right ) \in \mathsf {Sch}_{\mathrm {PA}}^{T}$
follows directly from Theorem 3 (since
$ \tau \in \mathsf {Sch}_{\mathsf {PA}}^{-}\Rightarrow \left ( \tau \wedge \tau _{\mathsf {PA}}\right ) \in \mathsf {Sch}_{\mathrm {PA}}^{T}$
follows directly from Theorem 3 (since
![]() ${\textsf {PA}}$
proves
${\textsf {PA}}$
proves
![]() $S _{\tau \wedge \tau _{{\textsf {PA}}}}$
if
$S _{\tau \wedge \tau _{{\textsf {PA}}}}$
if
![]() $\tau \in \mathrm {Sch}_{\mathsf {PA}}^{-}).$
On the other hand, if
$\tau \in \mathrm {Sch}_{\mathsf {PA}}^{-}).$
On the other hand, if
![]() $\left ( \tau \wedge \tau _{{\textsf {PA}}}\right ) \in \mathsf {Sch}_{{\textsf {PA}}}^{T}$
, then by the definition of
$\left ( \tau \wedge \tau _{{\textsf {PA}}}\right ) \in \mathsf {Sch}_{{\textsf {PA}}}^{T}$
, then by the definition of
![]() $\mathsf { Sch}_{\mathsf {PA}}^{T}$
,
$\mathsf { Sch}_{\mathsf {PA}}^{T}$
,
![]() ${\textsf {PA}}$
proves
${\textsf {PA}}$
proves
![]() $S _{\tau }$
, so
$S _{\tau }$
, so
![]() $\tau \in \mathsf {Sch}_{\mathsf {PA}}^{-}$
.
$\tau \in \mathsf {Sch}_{\mathsf {PA}}^{-}$
.
Finally, to establish
![]() $(iv)$
suppose
$(iv)$
suppose
![]() $\pi =\forall x\ \exists y\ \delta (x,y)$
is a
$\pi =\forall x\ \exists y\ \delta (x,y)$
is a
![]() $\Pi _{2}$
-statement, where
$\Pi _{2}$
-statement, where
![]() $ \delta (x,y)$
is
$ \delta (x,y)$
is
![]() $\Delta _{0}$
. In the proof of part (i) we showed that there are recursive functions f and g such that
$\Delta _{0}$
. In the proof of part (i) we showed that there are recursive functions f and g such that
Let h be the function that takes a template
![]() $\tau $
as input, and outputs the sentence
$\tau $
as input, and outputs the sentence
![]() $T[\tau ]\in \mathcal {L}_{T}$
expressing “T is
$T[\tau ]\in \mathcal {L}_{T}$
expressing “T is
![]() $\tau $
-correct.” Clearly h is a recursive function. Also, it is evident that
$\tau $
-correct.” Clearly h is a recursive function. Also, it is evident that
![]() $\tau \in \mathsf {Sch}_{\mathsf {PA}}^{-}$
iff
$\tau \in \mathsf {Sch}_{\mathsf {PA}}^{-}$
iff
![]() $T[\tau ]\in \mathsf {Cons}$
(the direction
$T[\tau ]\in \mathsf {Cons}$
(the direction
![]() $\Rightarrow $
follows from Theorem 8; and the direction
$\Rightarrow $
follows from Theorem 8; and the direction
![]() $\Leftarrow $
follows from the relevant definitions). Therefore,
$\Leftarrow $
follows from the relevant definitions). Therefore,
Proposition 27. Let
![]() $\varphi _s$
be the single
$\varphi _s$
be the single
![]() $\mathcal {L}_{T}$
-sentence that expresses “every
$\mathcal {L}_{T}$
-sentence that expresses “every
![]() ${\textsf {PA}}$
-provable scheme is true.” Then
${\textsf {PA}}$
-provable scheme is true.” Then
![]() $\mathsf {CT}_{0}$
can be axiomatized by
$\mathsf {CT}_{0}$
can be axiomatized by
![]() $\mathsf {CT}^{-}[{\textsf {EA}}]+\varphi _s$
.
$\mathsf {CT}^{-}[{\textsf {EA}}]+\varphi _s$
.
Proof By Theorem 6,
![]() $\mathsf {CT}_{0}$
can be axiomatized by
$\mathsf {CT}_{0}$
can be axiomatized by
![]() $\mathsf {CT}^{-}[{\textsf {EA}}]+\mathsf {GRP}({\textsf {PA}})$
. This makes it clear that
$\mathsf {CT}^{-}[{\textsf {EA}}]+\mathsf {GRP}({\textsf {PA}})$
. This makes it clear that
![]() $\varphi _s$
is provable in
$\varphi _s$
is provable in
![]() $\mathsf {CT}_{0}.$
For the other direction, working in
$\mathsf {CT}_{0}.$
For the other direction, working in
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + \varphi _s$
, suppose
${\textsf {CT}}^-[{\textsf {EA}}] + \varphi _s$
, suppose
![]() $\psi $
is
$\psi $
is
![]() ${\textsf {PA}}$
-provable. Then the scheme given by
${\textsf {PA}}$
-provable. Then the scheme given by
![]() $\forall x(\psi \vee P(x))$
is PA-provable, so the instance of this scheme in which P is replaced with
$\forall x(\psi \vee P(x))$
is PA-provable, so the instance of this scheme in which P is replaced with
![]() $x\neq x$
is true, but since
$x\neq x$
is true, but since
![]() $T(\forall x (x=x))$
, we have
$T(\forall x (x=x))$
, we have
![]() $T(\psi )$
. Thus, since
$T(\psi )$
. Thus, since
![]() $\psi $
was arbitrary,
$\psi $
was arbitrary,
![]() ${\textsf {CT}}^-[{\textsf {EA}}]+\varphi _s\vdash \mathsf {GRP}({\textsf {PA}}).$
${\textsf {CT}}^-[{\textsf {EA}}]+\varphi _s\vdash \mathsf {GRP}({\textsf {PA}}).$
3.2 Structure of schematically correct extensions
In this subsection we take a closer look at the structure of
![]() $\mathsf {Sch}_{{\textsf {PA}}}$
. In particular, we look at interpretability properties of its elements, where by “interpretability” we always mean relative interpretability, as described in [Reference Hájek and Pudlák9]. The most basic tool we shall use is a modification of the Vaught operation from the proof of Theorem 12. Let us introduce the relevant definition:
$\mathsf {Sch}_{{\textsf {PA}}}$
. In particular, we look at interpretability properties of its elements, where by “interpretability” we always mean relative interpretability, as described in [Reference Hájek and Pudlák9]. The most basic tool we shall use is a modification of the Vaught operation from the proof of Theorem 12. Let us introduce the relevant definition:
Definition 28. For arithmetical formulae
![]() $\varphi (x), \delta (x)$
with at most one free variable let the
$\varphi (x), \delta (x)$
with at most one free variable let the
![]() $\varphi $
-restricted Vaught schematization of
$\varphi $
-restricted Vaught schematization of
![]() $\delta $
be the scheme template.
$\delta $
be the scheme template.
For a single formula
![]() $\delta $
,
$\delta $
,
![]() $V_{\delta }[P]$
abbreviates
$V_{\delta }[P]$
abbreviates
![]() $V_{(x=x,\delta )}[P]$
and we often omit the reference to P. Similarly
$V_{(x=x,\delta )}[P]$
and we often omit the reference to P. Similarly
![]() $V_{\varphi ,\delta }[\theta (x)]$
abbreviates
$V_{\varphi ,\delta }[\theta (x)]$
abbreviates
![]() $V_{\varphi ,\delta }[\theta (x)/P(x)].$
$V_{\varphi ,\delta }[\theta (x)/P(x)].$
Convention 29. Working in
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
and having fixed an (possibly nonstandard) arithmetical formula with one free variable
${\textsf {CT}}^-[{\textsf {EA}}]$
and having fixed an (possibly nonstandard) arithmetical formula with one free variable
![]() $\theta (v)$
,
$\theta (v)$
,
![]() $T{*}\theta (x)$
will abbreviate the formula
$T{*}\theta (x)$
will abbreviate the formula
![]() $T(\theta [\underline {x}/v])$
. Hence
$T(\theta [\underline {x}/v])$
. Hence
![]() $T{*}\theta (x)$
says that x satisfies
$T{*}\theta (x)$
says that x satisfies
![]() $\theta $
. This notation was first introduced in [Reference Łełyk and Wcisło19] and is very successful in decreasing the number of brackets and improving readability.
$\theta $
. This notation was first introduced in [Reference Łełyk and Wcisło19] and is very successful in decreasing the number of brackets and improving readability.
Below, we shall borrow a notation used in the context of prudent axiomatizations:
![]() is the theory
is the theory
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + T[\tau ]$
, i.e.,
${\textsf {CT}}^-[{\textsf {EA}}] + T[\tau ]$
, i.e.,
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
together with the assertion that T is
${\textsf {CT}}^-[{\textsf {EA}}]$
together with the assertion that T is
![]() $\tau $
-correct. In such contexts the variables such as
$\tau $
-correct. In such contexts the variables such as
![]() $\sigma $
,
$\sigma $
,
![]() $\tau $
, or
$\tau $
, or
![]() $V_{--}$
below will always denote scheme templates.
$V_{--}$
below will always denote scheme templates.
Theorem 30. If
![]() $\psi \in \mathcal {L}_T$
is such that for every
$\psi \in \mathcal {L}_T$
is such that for every
![]() $\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
,
$\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
,
![]() $\psi $
is interpretable in
$\psi $
is interpretable in
![]() , then
, then
![]() $\psi $
is interpretable in
$\psi $
is interpretable in
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
.
${\textsf {CT}}^-[{\textsf {PA}}]$
.
Proof We prove the contrapositive. Fix
![]() $\psi $
which is not interpretable in
$\psi $
which is not interpretable in
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
. We modify the Pakhomov–Visser diagonalization from [Reference Pakhomov and Visser22, Theorem 4.1]. Observe that for two finite theories
${\textsf {CT}}^-[{\textsf {PA}}]$
. We modify the Pakhomov–Visser diagonalization from [Reference Pakhomov and Visser22, Theorem 4.1]. Observe that for two finite theories
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
, the condition “
$\beta $
, the condition “
![]() $\alpha $
interprets
$\alpha $
interprets
![]() $\beta $
” is
$\beta $
” is
![]() $\Sigma _1$
. Let
$\Sigma _1$
. Let
![]() $\alpha \triangleright \beta $
denote the formalization of this relation. Consider a
$\alpha \triangleright \beta $
denote the formalization of this relation. Consider a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\varphi = \exists x \varphi '(x)$
, where
$\varphi = \exists x \varphi '(x)$
, where
![]() $\varphi '(x)\in \Delta _0$
such that the following equivalence is provable in
$\varphi '(x)\in \Delta _0$
such that the following equivalence is provable in
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
:
${\textsf {CT}}^-[{\textsf {PA}}]$
:
Similarly to the Pakhomov–Visser argument, we argue that
![]() $\varphi $
is false. Suppose not and take the least
$\varphi $
is false. Suppose not and take the least
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $\varphi '(n)$
holds. Then, in
$\varphi '(n)$
holds. Then, in
![]() ${\textsf {Q}}$
,
${\textsf {Q}}$
,
![]() $\forall z \leq x\neg \varphi '(z)$
is equivalent to
$\forall z \leq x\neg \varphi '(z)$
is equivalent to
![]() $x< \underline {n}$
, hence the following is provable in
$x< \underline {n}$
, hence the following is provable in
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
:
${\textsf {CT}}^-[{\textsf {PA}}]$
:
We claim that
Indeed, working in
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
fix
${\textsf {CT}}^-[{\textsf {PA}}]$
fix
![]() $\theta \in {\textsf {Form}}^{\leq 1}_{\mathcal {L}_{{\textsf {PA}}}}$
. By compositional conditions
$\theta \in {\textsf {Form}}^{\leq 1}_{\mathcal {L}_{{\textsf {PA}}}}$
. By compositional conditions
![]() $T\bigl (V_{(y< \underline {n}, \delta _{{\textsf {PA}}})}[\theta ]\bigr )$
is equivalent to
$T\bigl (V_{(y< \underline {n}, \delta _{{\textsf {PA}}})}[\theta ]\bigr )$
is equivalent to
However, once again by compositional conditions imposed on T,
![]() $T{*}\text {True}(\underline {i}, \theta )$
is equivalent to
$T{*}\text {True}(\underline {i}, \theta )$
is equivalent to
![]() $\text {True}(\underline {i}, T{*}\theta (x))$
, hence to the assertion that
$\text {True}(\underline {i}, T{*}\theta (x))$
, hence to the assertion that
![]() $T{*}\theta (x)$
is a compositional truth predicate for formulae of depth at most i. Assuming that this is the case, since i is standard, every induction axiom of pure depth at most i is true in the sense of
$T{*}\theta (x)$
is a compositional truth predicate for formulae of depth at most i. Assuming that this is the case, since i is standard, every induction axiom of pure depth at most i is true in the sense of
![]() $T{*}\theta (x)$
. This concludes our proof of (*).
$T{*}\theta (x)$
. This concludes our proof of (*).
Now, since
![]() $\varphi $
is true, it follows that
$\varphi $
is true, it follows that
However, by the above argument it would mean that
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
interprets
${\textsf {CT}}^-[{\textsf {PA}}]$
interprets
![]() $\psi $
, contrary to the assumption.
$\psi $
, contrary to the assumption.
Since
![]() $\varphi $
is false,
$\varphi $
is false,
![]() $V_{(\forall z \leq y \neg \varphi '(z),\delta _{{\textsf {PA}}})}[P]$
is a scheme template, such that the scheme associated with it axiomatizes
$V_{(\forall z \leq y \neg \varphi '(z),\delta _{{\textsf {PA}}})}[P]$
is a scheme template, such that the scheme associated with it axiomatizes
![]() ${\textsf {PA}}$
. Moreover,
${\textsf {PA}}$
. Moreover,
![]() ${\textsf {CT}}^-[{\textsf {PA}}] + T\bigl [V_{(\forall z\leq y\neg \varphi '(z),\delta _{{\textsf {PA}}})}\bigr ]$
does not interpret
${\textsf {CT}}^-[{\textsf {PA}}] + T\bigl [V_{(\forall z\leq y\neg \varphi '(z),\delta _{{\textsf {PA}}})}\bigr ]$
does not interpret
![]() $\psi $
.
$\psi $
.
Since
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
is interpretable in
${\textsf {CT}}^-[{\textsf {PA}}]$
is interpretable in
![]() ${\textsf {PA}}$
(see [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7, Reference Leigh15]), we obtain the following corollary.
${\textsf {PA}}$
(see [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7, Reference Leigh15]), we obtain the following corollary.
Corollary 31. For every
![]() $\psi \in \mathcal {L}_T$
such that
$\psi \in \mathcal {L}_T$
such that
![]() ${\textsf {PA}}$
does not interpret
${\textsf {PA}}$
does not interpret
![]() $\psi $
there is a scheme template
$\psi $
there is a scheme template
![]() $\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
such that
$\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
such that
![]() does not relatively interpret
does not relatively interpret
![]() $\psi $
.
$\psi $
.
Since
![]() ${\textsf {PA}}\ntriangleright \mathsf {Q}+{\textsf {Con}}_{{\textsf {PA}}}$
(see [Reference Pudlák26]) we obtain the following corollary. It is of interest because it gives an example of a natural theory that is not interpretable in
${\textsf {PA}}\ntriangleright \mathsf {Q}+{\textsf {Con}}_{{\textsf {PA}}}$
(see [Reference Pudlák26]) we obtain the following corollary. It is of interest because it gives an example of a natural theory that is not interpretable in
![]() ${\textsf {PA}}$
(because it is finite) but this is not due to the reason that the theory interprets the consistency of
${\textsf {PA}}$
(because it is finite) but this is not due to the reason that the theory interprets the consistency of
![]() ${\textsf {PA}}$
(like most known finite extensions of
${\textsf {PA}}$
(like most known finite extensions of
![]() ${\textsf {PA}}$
).
${\textsf {PA}}$
).
Corollary 32. There is a scheme template
![]() $\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
such that
$\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
such that
![]() does not interpret
does not interpret
![]() ${\textsf {Q}}+{\textsf {Con}}_{{\textsf {PA}}}$
.
${\textsf {Q}}+{\textsf {Con}}_{{\textsf {PA}}}$
.
Corollary 33. For every scheme template
![]() $\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
there is a scheme template
$\tau \in \mathsf {Sch}_{{\textsf {PA}}}$
there is a scheme template
![]() $\tau '\in \mathsf {Sch}_{{\textsf {PA}}}$
such that
$\tau '\in \mathsf {Sch}_{{\textsf {PA}}}$
such that
![]() interprets
interprets
![]() , but not vice versa.
, but not vice versa.
Proof Fix
![]() $\tau $
and apply Corollary 31 to
$\tau $
and apply Corollary 31 to
![]() . This is legal, since the latter theory is a finitely axiomatizable extension of
. This is legal, since the latter theory is a finitely axiomatizable extension of
![]() ${\textsf {PA}}$
, hence it is not interpretable in
${\textsf {PA}}$
, hence it is not interpretable in
![]() ${\textsf {PA}}$
.Footnote
10
So there is a scheme
${\textsf {PA}}$
.Footnote
10
So there is a scheme
![]() $\tau "\in \mathsf {Sch}_{{\textsf {PA}}}$
such that
$\tau "\in \mathsf {Sch}_{{\textsf {PA}}}$
such that
![]() does not relatively interpret
does not relatively interpret
![]() . Now it is sufficient to take
. Now it is sufficient to take
![]() $\tau ':= \tau \otimes \tau "$
, as in the proof of Proposition 23.
$\tau ':= \tau \otimes \tau "$
, as in the proof of Proposition 23.
Next we will consider more structural properties of
![]() $\mathsf {Sch}_{{\textsf {PA}}}$
. These properties will be shown to be transferable to the Lindenbaum Algebra of
$\mathsf {Sch}_{{\textsf {PA}}}$
. These properties will be shown to be transferable to the Lindenbaum Algebra of
![]() ${\textsf {CT}}_0$
.
${\textsf {CT}}_0$
.
-
• For the rest of this section
 $\delta $
and
$\delta $
and
 $\delta '$
are arbitrary elementary formulae that, provably in
$\delta '$
are arbitrary elementary formulae that, provably in
 ${\textsf {EA}}$
, specify arithmetical theories, i.e., possibly infinite sets of arithmetical sentences. We will write
${\textsf {EA}}$
, specify arithmetical theories, i.e., possibly infinite sets of arithmetical sentences. We will write
 $\delta \subseteq \delta '$
as an abbreviation of
$\delta \subseteq \delta '$
as an abbreviation of
 $\forall x (\delta (x) \rightarrow \delta '(x))$
. Recall (from Definition 17) that
$\forall x (\delta (x) \rightarrow \delta '(x))$
. Recall (from Definition 17) that
 $T[\delta ]$
is the following sentence expressing “T is
$T[\delta ]$
is the following sentence expressing “T is
 $\delta $
correct”: Note the difference between
$\delta $
correct”: Note the difference between $$\begin{align*}\forall x \bigl(\delta(x)\rightarrow T(x)\bigr).\end{align*}$$
$$\begin{align*}\forall x \bigl(\delta(x)\rightarrow T(x)\bigr).\end{align*}$$
 $T[V_{\delta }]$
and
$T[V_{\delta }]$
and
 $T[\delta ]$
.
$T[\delta ]$
.
The first result is immediate:
Proposition 34. For every
![]() $\delta $
and
$\delta $
and
![]() $\delta '$
,
$\delta '$
,
![]() ${\textsf {CT}}^-[{\textsf {PA}}]\vdash \forall x \bigl (\delta (x)\rightarrow \delta '(x)\bigr )\rightarrow \bigl (T[V_{\delta '}]\rightarrow T[V_{\delta }]\bigr ).$
${\textsf {CT}}^-[{\textsf {PA}}]\vdash \forall x \bigl (\delta (x)\rightarrow \delta '(x)\bigr )\rightarrow \bigl (T[V_{\delta '}]\rightarrow T[V_{\delta }]\bigr ).$
For many applications, the condition
![]() $\delta \subseteq \delta '$
from the antecedent is too restrictive. One would like to relax it to
$\delta \subseteq \delta '$
from the antecedent is too restrictive. One would like to relax it to
![]() $\delta \vdash \delta '$
, however, this one is too weak to guarantee (over
$\delta \vdash \delta '$
, however, this one is too weak to guarantee (over
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
) that the implication
${\textsf {CT}}^-[{\textsf {PA}}]$
) that the implication
![]() $T[V_{\delta '}]\rightarrow T[V_{\delta }]$
holds. This is because the truth predicate axiomatized by pure
$T[V_{\delta '}]\rightarrow T[V_{\delta }]$
holds. This is because the truth predicate axiomatized by pure
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
is far from being closed under logic (compare with Theorem 6). The next proposition is a fair compromise between the two solutions.
${\textsf {CT}}^-[{\textsf {PA}}]$
is far from being closed under logic (compare with Theorem 6). The next proposition is a fair compromise between the two solutions.
-
• Given a unary arithmetical formula
 $\varphi (x)$
, in the proposition below we use the convention of using
$\varphi (x)$
, in the proposition below we use the convention of using
 $\delta _{\varphi }(x)$
to refer to the formula that defines the set of (codes of) sentences of the form
$\delta _{\varphi }(x)$
to refer to the formula that defines the set of (codes of) sentences of the form
 $\varphi (\underline {n})$
(in the standard model
$\varphi (\underline {n})$
(in the standard model
 $\mathbb {N}$
of arithmetic).
$\mathbb {N}$
of arithmetic).
Proposition 35. For arbitrary arithmetical formulae
![]() $\varphi (x)$
and
$\varphi (x)$
and
![]() $\psi (x),$
$\psi (x),$
Proof Fix arbitrary arithmetical formulae
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
with exactly one free variable. Let
$\varphi $
with exactly one free variable. Let
![]() $\delta _{\psi }$
and
$\delta _{\psi }$
and
![]() $\delta _{\varphi }$
be defined in the bullet point above the current proposition. Without loss of generality, assume that the variable x occurs in
$\delta _{\varphi }$
be defined in the bullet point above the current proposition. Without loss of generality, assume that the variable x occurs in
![]() $\psi $
. Working in
$\psi $
. Working in
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
assume that
${\textsf {CT}}^-[{\textsf {PA}}]$
assume that
![]() $\forall x \bigl (\varphi (x)\rightarrow \psi (x)\bigr )$
and
$\forall x \bigl (\varphi (x)\rightarrow \psi (x)\bigr )$
and
![]() $T[V_{\delta _{\varphi }}]$
hold. We argue that
$T[V_{\delta _{\varphi }}]$
hold. We argue that
![]() $T[V_{\delta _{\psi }}]$
holds as well. Fix arbitrary a,
$T[V_{\delta _{\psi }}]$
holds as well. Fix arbitrary a,
![]() $\theta $
, b such that
$\theta $
, b such that
![]() $\mathsf {True}(a,T{*}\theta )$
and
$\mathsf {True}(a,T{*}\theta )$
and
![]() $\textsf {pdepth}(\psi (\underline {b}))\leq a$
. It follows that for some standard n,
$\textsf {pdepth}(\psi (\underline {b}))\leq a$
. It follows that for some standard n,
![]() $\textsf {pdepth}(\varphi (\underline {b}))\leq a+n$
, hence there exists a formula
$\textsf {pdepth}(\varphi (\underline {b}))\leq a+n$
, hence there exists a formula
![]() $\theta '(x)$
such that
$\theta '(x)$
such that
By
![]() $T[V_{\delta _{\varphi }}]$
we conclude
$T[V_{\delta _{\varphi }}]$
we conclude
![]() $T{*}\theta '(\varphi (\underline {b})).$
However, since
$T{*}\theta '(\varphi (\underline {b})).$
However, since
![]() $\varphi (x)$
is of standard depth, it follows that
$\varphi (x)$
is of standard depth, it follows that
![]() $\varphi (b)$
holds. Hence
$\varphi (b)$
holds. Hence
![]() $\psi (b)$
holds as well. Since
$\psi (b)$
holds as well. Since
![]() $\psi (b)$
is also of standard depth, we conclude that
$\psi (b)$
is also of standard depth, we conclude that
![]() $T{*}\theta (\psi (\underline {b}))$
, which ends the proof.
$T{*}\theta (\psi (\underline {b}))$
, which ends the proof.
The proposition below is an important tool for discovering various patterns in
![]() $\mathsf {Sch}_{{\textsf {PA}}}$
. It enables us to switch from somewhat less readable Vaught schematizations of elementary presentations of theories to more workable presentations themselves. It says that over
$\mathsf {Sch}_{{\textsf {PA}}}$
. It enables us to switch from somewhat less readable Vaught schematizations of elementary presentations of theories to more workable presentations themselves. It says that over
![]() ${\textsf {CT}}_0$
,
${\textsf {CT}}_0$
,
![]() $\delta $
-correctness is equivalent to
$\delta $
-correctness is equivalent to
![]() $V_{\delta }$
-correctness.
$V_{\delta }$
-correctness.
Proposition 36. For every
![]() $\delta $
,
$\delta $
,
![]() ${\textsf {CT}}_0\vdash T[\delta ]\leftrightarrow T[V_{\delta }].$
${\textsf {CT}}_0\vdash T[\delta ]\leftrightarrow T[V_{\delta }].$
Proof We start by showing that provably in
![]() ${\textsf {CT}}_0$
all arithmetical partial truth predicates are coextensive, i.e., the following is provable in
${\textsf {CT}}_0$
all arithmetical partial truth predicates are coextensive, i.e., the following is provable in
![]() ${\textsf {CT}}_0$
:
${\textsf {CT}}_0$
:
Fix an arbitrary
![]() $(\mathcal {M},T)\models {\textsf {CT}}_0$
. For an arbitrary
$(\mathcal {M},T)\models {\textsf {CT}}_0$
. For an arbitrary
![]() $c\in M$
, let
$c\in M$
, let
![]() $T_c$
denote the (
$T_c$
denote the (
![]() $(\mathcal {M},T)$
-definable) restriction of T to all sentences of depth at most c. Then
$(\mathcal {M},T)$
-definable) restriction of T to all sentences of depth at most c. Then
![]() $(\mathcal {M},T_c)\models \mathsf {True}(c,T)$
. However, as proved in [Reference Łełyk and Wcisło20, Fact 32],
$(\mathcal {M},T_c)\models \mathsf {True}(c,T)$
. However, as proved in [Reference Łełyk and Wcisło20, Fact 32],
![]() $(\mathcal {M},T_c)$
satisfies full induction scheme for
$(\mathcal {M},T_c)$
satisfies full induction scheme for
![]() $\mathcal {L}_T$
. Hence
$\mathcal {L}_T$
. Hence
![]() $T_c$
is a fully inductive truth predicate for formulae of depth at most c. Using this we argue that (*) holds in
$T_c$
is a fully inductive truth predicate for formulae of depth at most c. Using this we argue that (*) holds in
![]() $(\mathcal {M},T)$
. Working in the model, fix an arbitrary a and an arbitrary
$(\mathcal {M},T)$
. Working in the model, fix an arbitrary a and an arbitrary
![]() $\theta \in {\textsf {Form}}^{\leq 1}_{\mathcal {L}_{{\textsf {PA}}}}$
. Assume that the depth of
$\theta \in {\textsf {Form}}^{\leq 1}_{\mathcal {L}_{{\textsf {PA}}}}$
. Assume that the depth of
![]() $\theta $
is b and let
$\theta $
is b and let
![]() $c = \max \{a,b\}$
. Assume
$c = \max \{a,b\}$
. Assume
![]() $\mathsf {True}(a,T{*}\theta )$
, i.e. the formula
$\mathsf {True}(a,T{*}\theta )$
, i.e. the formula
![]() $T{*}\theta $
is a partial truth predicate for formulae of depth
$T{*}\theta $
is a partial truth predicate for formulae of depth
![]() $\leq a$
. Since for every formula
$\leq a$
. Since for every formula
![]() $\varphi $
of depth at most c,
$\varphi $
of depth at most c,
![]() $T_c(\varphi )$
is equivalent to
$T_c(\varphi )$
is equivalent to
![]() $T(\varphi )$
, we conclude that
$T(\varphi )$
, we conclude that
![]() $\mathsf {True}(a, T_c{*}\theta )$
holds. Moreover, it is sufficient to show that
$\mathsf {True}(a, T_c{*}\theta )$
holds. Moreover, it is sufficient to show that
In other words, it is sufficient to prove that
The above can be demonstrated by a routine induction on the build-up of formulae. More precisely, let
Then
![]() $\Xi (0)$
and
$\Xi (0)$
and
![]() $\forall x<a \bigl (\Xi (x)\rightarrow \Xi (x+1)\bigr )$
hold (in
$\forall x<a \bigl (\Xi (x)\rightarrow \Xi (x+1)\bigr )$
hold (in
![]() $(\mathcal {M}, T_c)$
), because both
$(\mathcal {M}, T_c)$
), because both
![]() $T_c{*}\theta $
and
$T_c{*}\theta $
and
![]() $T_c$
are partial truth predicates for formulae of depth at most a. Since
$T_c$
are partial truth predicates for formulae of depth at most a. Since
![]() $\Xi (y)$
is a formula of
$\Xi (y)$
is a formula of
![]() $\mathcal {L}_T$
, in
$\mathcal {L}_T$
, in
![]() $(\mathcal {M},T_c)$
we have an induction axiom for it, and we can conclude
$(\mathcal {M},T_c)$
we have an induction axiom for it, and we can conclude
This completes the proof of (*).
We show that over
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
,
${\textsf {CT}}^-[{\textsf {PA}}]$
,
![]() $T[\delta ]$
implies
$T[\delta ]$
implies
![]() $T[V_{\delta }]$
. We fix an arbitrary
$T[V_{\delta }]$
. We fix an arbitrary
![]() $\delta $
and working in
$\delta $
and working in
![]() ${\textsf {CT}}_0$
assume that
${\textsf {CT}}_0$
assume that
![]() $\forall x \bigl (\delta (x)\rightarrow T(x)\bigr )$
. We show that T is
$\forall x \bigl (\delta (x)\rightarrow T(x)\bigr )$
. We show that T is
![]() $V_{\delta }$
-correct, i.e., for every arithmetical formula
$V_{\delta }$
-correct, i.e., for every arithmetical formula
![]() $\theta $
(possibly nonstandard)
$\theta $
(possibly nonstandard)
![]() $T(V_{\delta }[\theta ])$
holds. By the compositional conditions,
$T(V_{\delta }[\theta ])$
holds. By the compositional conditions,
![]() $T(V_{\delta }[\theta ])$
is equivalent to
$T(V_{\delta }[\theta ])$
is equivalent to
Fix x, assume
![]() $\mathsf {True}(x, T{*}\theta )$
and fix an arbitrary y such that
$\mathsf {True}(x, T{*}\theta )$
and fix an arbitrary y such that
![]() $\textsf {pdepth}(y)\leq x$
and
$\textsf {pdepth}(y)\leq x$
and
![]() $\delta (y)$
. By
$\delta (y)$
. By
![]() $\delta $
-correctness
$\delta $
-correctness
![]() $T(y)$
holds, hence y is a formula and since
$T(y)$
holds, hence y is a formula and since
![]() $\textsf {pdepth}(y)\leq x$
, y is a formula of depth at most x. Then, by the previous claim (*) we know that for every
$\textsf {pdepth}(y)\leq x$
, y is a formula of depth at most x. Then, by the previous claim (*) we know that for every
![]() $\varphi $
whose depth is at most x,
$\varphi $
whose depth is at most x,
![]() $T{*}\theta (\varphi )$
is equivalent to
$T{*}\theta (\varphi )$
is equivalent to
![]() $T(\varphi )$
. Hence
$T(\varphi )$
. Hence
![]() $T{*}\theta (y)$
holds as well.
$T{*}\theta (y)$
holds as well.
For the converse direction, we assume T is
![]() $V_{\delta }$
-correct. Fix an arbitrary x and assume that
$V_{\delta }$
-correct. Fix an arbitrary x and assume that
![]() $\delta (x)$
holds. In particular x is a formula. Let y be the depth of x and let
$\delta (x)$
holds. In particular x is a formula. Let y be the depth of x and let
![]() $\theta $
be any arithmetical truth predicate such that
$\theta $
be any arithmetical truth predicate such that
![]() ${\textsf {Pr}}_{{\textsf {PA}}}(\mathsf {True}(\underline {y},\theta ))$
holds. By the Global Reflection in
${\textsf {Pr}}_{{\textsf {PA}}}(\mathsf {True}(\underline {y},\theta ))$
holds. By the Global Reflection in
![]() ${\textsf {CT}}_0$
,
${\textsf {CT}}_0$
,
![]() $T(\mathsf {True}(\underline {y},\theta ))$
holds as well, and this in turn implies, by compositional conditions,
$T(\mathsf {True}(\underline {y},\theta ))$
holds as well, and this in turn implies, by compositional conditions,
![]() $\mathsf {True}(y, T{*}\theta )$
. Consequently, by
$\mathsf {True}(y, T{*}\theta )$
. Consequently, by
![]() $V_{\delta }$
-correctness,
$V_{\delta }$
-correctness,
![]() $T{*}\theta (x)$
holds. Finally, it follows that
$T{*}\theta (x)$
holds. Finally, it follows that
![]() $T(x)$
holds by our claim (*). This concludes the proof of
$T(x)$
holds by our claim (*). This concludes the proof of
![]() $\delta $
-correctness and the whole proof.
$\delta $
-correctness and the whole proof.
Corollary 37. For every
![]() $\delta ,\delta '$
, if
$\delta ,\delta '$
, if
![]() ${\textsf {CT}}^-[{\textsf {EA}}]\vdash T[V_{\delta }]\rightarrow T[V_{\delta '}]$
, then
${\textsf {CT}}^-[{\textsf {EA}}]\vdash T[V_{\delta }]\rightarrow T[V_{\delta '}]$
, then
![]() ${\textsf {CT}}_0\vdash T[\delta ]\rightarrow T[\delta '].$
${\textsf {CT}}_0\vdash T[\delta ]\rightarrow T[\delta '].$
The above corollary yields a versatile tool for studying the structure of
![]() $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
, where
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
, where
![]() $\leq _{{\textsf {CT}}^-}$
is defined by:
$\leq _{{\textsf {CT}}^-}$
is defined by:
![]() $\tau _{1} \leq _{{\textsf {CT}}^-} \tau _{2}$
iff
$\tau _{1} \leq _{{\textsf {CT}}^-} \tau _{2}$
iff
![]() ${\textsf {CT}}^-[{\textsf {EA}}] \vdash T[\tau _{1}]\rightarrow T[\tau _{2}]$
. We show the crucial application:
${\textsf {CT}}^-[{\textsf {EA}}] \vdash T[\tau _{1}]\rightarrow T[\tau _{2}]$
. We show the crucial application:
Theorem 38.
![]() $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
is a countably universal partial order.
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
is a countably universal partial order.
We recall that a partial order
![]() $\langle P, \leq _P\rangle $
is said to be countably universal if every countable partial order
$\langle P, \leq _P\rangle $
is said to be countably universal if every countable partial order
![]() $\langle Q, \leq _Q\rangle $
can be embedded into
$\langle Q, \leq _Q\rangle $
can be embedded into
![]() $\langle P, \leq _P\rangle $
, i.e., there is an injection
$\langle P, \leq _P\rangle $
, i.e., there is an injection
![]() $f:Q\rightarrow P$
such that for every
$f:Q\rightarrow P$
such that for every
![]() $a,b\in P$
,
$a,b\in P$
,
![]() $f(a)\leq _P f(b) \iff a\leq _Q b$
.
$f(a)\leq _P f(b) \iff a\leq _Q b$
.
The above theorem reduces immediately to the one below.Footnote
11
This is thanks to the work of Hubička and Nešetřil [Reference Hubička and Nešetřil11, Corollary 2.6], where a particular countably universal partial order is defined. It is clear from the presentation that the order
![]() $\langle \mathcal {W}, \leq _{\mathcal {W}}\rangle $
is decidable and provably a partial order in
$\langle \mathcal {W}, \leq _{\mathcal {W}}\rangle $
is decidable and provably a partial order in
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
Theorem 39. Suppose that
![]() $\preceq $
is a decidable partial order on
$\preceq $
is a decidable partial order on
![]() $\omega $
such that
$\omega $
such that
![]() ${\textsf {PA}}$
proves that
${\textsf {PA}}$
proves that
![]() $\preceq $
is a partial order. Then there is an embedding
$\preceq $
is a partial order. Then there is an embedding
![]() $\langle \omega , \preceq \rangle \hookrightarrow \langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
.
$\langle \omega , \preceq \rangle \hookrightarrow \langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
.
Proof Suppose that
![]() $\preceq $
satisfies the assumptions. Firstly, we build a family of consistent theories
$\preceq $
satisfies the assumptions. Firstly, we build a family of consistent theories
![]() $\{\sigma _n\}_{n\in \omega }$
such that the following hold for all
$\{\sigma _n\}_{n\in \omega }$
such that the following hold for all
![]() $m,n \in \omega $
:
$m,n \in \omega $
:
-
1. If
 $m\preceq n$
, then
$m\preceq n$
, then
 ${\textsf {PA}}\vdash \sigma _n\subseteq \sigma _m$
.
${\textsf {PA}}\vdash \sigma _n\subseteq \sigma _m$
. -
2.
 ${\textsf {CT}}_0\nvdash {\textsf {Con}}_{\sigma _m}$
.
${\textsf {CT}}_0\nvdash {\textsf {Con}}_{\sigma _m}$
. -
3. If
 $m\npreceq n$
, then
$m\npreceq n$
, then
 ${\textsf {CT}}_0+{\textsf {Con}}_{\sigma _m}\nvdash {\textsf {Con}}_{\sigma _n}$
.
${\textsf {CT}}_0+{\textsf {Con}}_{\sigma _m}\nvdash {\textsf {Con}}_{\sigma _n}$
.
As shown in [Reference Lindström21, Section 2.3, Theorem 11], there is a
![]() $\Pi _1$
-formula
$\Pi _1$
-formula
![]() $\pi (x)$
that is flexible over
$\pi (x)$
that is flexible over
![]() $\mathsf {REF}^{<\omega }({\textsf {PA}})$
, i.e., for every
$\mathsf {REF}^{<\omega }({\textsf {PA}})$
, i.e., for every
![]() $\Pi _1$
-formula
$\Pi _1$
-formula
![]() $\theta (x)$
, the following theory is consistent:
$\theta (x)$
, the following theory is consistent:
For each
![]() $n\in \omega $
let
$n\in \omega $
let
![]() $\sigma _n$
be the natural
$\sigma _n$
be the natural
![]() $\Sigma _1$
-definition of the following set of sentencesFootnote
12
:
$\Sigma _1$
-definition of the following set of sentencesFootnote
12
:
Now, condition (1) easily follows from the (
![]() ${\textsf {PA}}$
-provable) transitivity of
${\textsf {PA}}$
-provable) transitivity of
![]() $\preceq $
. Condition (2) easily reduces to Condition (3), so let us now show the latter. Aiming at a contradiction assume
$\preceq $
. Condition (2) easily reduces to Condition (3), so let us now show the latter. Aiming at a contradiction assume
![]() $m\npreceq n$
and
$m\npreceq n$
and
![]() ${\textsf {CT}}_0\vdash {\textsf {Con}}_{\sigma _m}\rightarrow {\textsf {Con}}_{\sigma _n}$
. Let
${\textsf {CT}}_0\vdash {\textsf {Con}}_{\sigma _m}\rightarrow {\textsf {Con}}_{\sigma _n}$
. Let
![]() $\theta (x):= m\preceq x$
. By flexibility there exists model
$\theta (x):= m\preceq x$
. By flexibility there exists model
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
By the choice of
![]() $\mathcal {M}$
it follows that
$\mathcal {M}$
it follows that
![]() $\mathcal {M}\models \neg \pi (n)$
. As a consequence, by provable
$\mathcal {M}\models \neg \pi (n)$
. As a consequence, by provable
![]() $\Sigma _1$
-completeness of
$\Sigma _1$
-completeness of
![]() ${\textsf {PA}}$
,
${\textsf {PA}}$
,
![]() $\mathcal {M}\models {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi (\underline {n})),$
and
$\mathcal {M}\models {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi (\underline {n})),$
and
![]() $\mathcal {M}\models \neg {\textsf {Con}}_{\sigma _{n}}$
. However, since
$\mathcal {M}\models \neg {\textsf {Con}}_{\sigma _{n}}$
. However, since
![]() $\mathcal {M}\models \mathsf {REF}({\textsf {PA}})$
, as viewed in
$\mathcal {M}\models \mathsf {REF}({\textsf {PA}})$
, as viewed in
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() ${\textsf {PA}}$
is consistent with
${\textsf {PA}}$
is consistent with
![]() $\Pi _1$
-truth (of
$\Pi _1$
-truth (of
![]() $\mathcal {M}$
). Consequently, since
$\mathcal {M}$
). Consequently, since
![]() $\mathcal {M}\models \forall x\bigl ( m\preceq x \rightarrow \pi (x)\bigr )$
, it follows that
$\mathcal {M}\models \forall x\bigl ( m\preceq x \rightarrow \pi (x)\bigr )$
, it follows that
![]() $\mathcal {M}\models {\textsf {Con}}_{\sigma _{m}}$
. Hence
$\mathcal {M}\models {\textsf {Con}}_{\sigma _{m}}$
. Hence
![]() $\mathcal {M}\models {\textsf {Con}}_{\sigma _n}$
as well, which contradicts our previous conclusions.
$\mathcal {M}\models {\textsf {Con}}_{\sigma _n}$
as well, which contradicts our previous conclusions.
We are ready to construct the promised embedding. Fix the family
![]() $\{\sigma _n\}_{n\in \omega }$
as above and for each
$\{\sigma _n\}_{n\in \omega }$
as above and for each
![]() $m\in \omega $
choose
$m\in \omega $
choose
![]() $\delta _m \in \Delta ^*$
to be the natural elementary definition of the following set of sentences:
$\delta _m \in \Delta ^*$
to be the natural elementary definition of the following set of sentences:
where
![]() ${\textsf {Con}}_{\sigma _m}(\underline {n})$
asserts that there is no proof of contradiction of
${\textsf {Con}}_{\sigma _m}(\underline {n})$
asserts that there is no proof of contradiction of
![]() $\sigma _m$
with Gödel code
$\sigma _m$
with Gödel code
![]() $\leq n$
. Since for every
$\leq n$
. Since for every
![]() $m \in \omega $
,
$m \in \omega $
,
![]() $\sigma _m$
is consistent,
$\sigma _m$
is consistent,
![]() $\delta _m$
is really an axiomatization of
$\delta _m$
is really an axiomatization of
![]() ${\textsf {PA}}$
, hence
${\textsf {PA}}$
, hence
![]() $V_{\delta _m}\in \mathsf {Sch}_{{\textsf {PA}}}$
. We check that the map
$V_{\delta _m}\in \mathsf {Sch}_{{\textsf {PA}}}$
. We check that the map
is an embedding of
![]() $\langle \omega , \preceq \rangle $
into
$\langle \omega , \preceq \rangle $
into
![]() $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle .$
Fix
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle .$
Fix
![]() $m,n\in \omega $
and assume
$m,n\in \omega $
and assume
![]() $m\preceq n$
. Then clearly
$m\preceq n$
. Then clearly
![]() ${\textsf {PA}}\vdash \forall x \bigl ({\textsf {Con}}_{\sigma _m}(x)\rightarrow {\textsf {Con}}_{\sigma _n}(x)\bigr )$
. Consequently, applying Proposition 35 to
${\textsf {PA}}\vdash \forall x \bigl ({\textsf {Con}}_{\sigma _m}(x)\rightarrow {\textsf {Con}}_{\sigma _n}(x)\bigr )$
. Consequently, applying Proposition 35 to
![]() $\varphi (x):= {\textsf {Con}}_{\sigma _m}(x)$
and
$\varphi (x):= {\textsf {Con}}_{\sigma _m}(x)$
and
![]() $\psi (x):= {\textsf {Con}}_{\sigma _n}(x)$
, we obtain
$\psi (x):= {\textsf {Con}}_{\sigma _n}(x)$
, we obtain
Suppose now
![]() $m\npreceq n$
and aiming at a contradiction, assume that
$m\npreceq n$
and aiming at a contradiction, assume that
![]() ${\textsf {CT}}^-[{\textsf {PA}}]\vdash T[V_{\delta _m}]\rightarrow T[V_{\delta _n}]$
. Then, by Corollary 37,
${\textsf {CT}}^-[{\textsf {PA}}]\vdash T[V_{\delta _m}]\rightarrow T[V_{\delta _n}]$
. Then, by Corollary 37,
![]() ${\textsf {CT}}_0\vdash T[\delta _m]\rightarrow T[\delta _n]$
. However, since
${\textsf {CT}}_0\vdash T[\delta _m]\rightarrow T[\delta _n]$
. However, since
![]() ${\textsf {CT}}_0 \vdash T[\delta _{{\textsf {PA}}}]$
,
${\textsf {CT}}_0 \vdash T[\delta _{{\textsf {PA}}}]$
,
![]() ${\textsf {CT}}_0\vdash T[\delta _i]\leftrightarrow {\textsf {Con}}_{\sigma _i}$
for every
${\textsf {CT}}_0\vdash T[\delta _i]\leftrightarrow {\textsf {Con}}_{\sigma _i}$
for every
![]() $i\in \omega $
. Hence
$i\in \omega $
. Hence
![]() ${\textsf {CT}}_0\vdash {\textsf {Con}}_{\sigma _m}\rightarrow {\textsf {Con}}_{\sigma _n}$
, which is impossible by our previous considerations, since
${\textsf {CT}}_0\vdash {\textsf {Con}}_{\sigma _m}\rightarrow {\textsf {Con}}_{\sigma _n}$
, which is impossible by our previous considerations, since
![]() $m\npreceq n$
.
$m\npreceq n$
.
Corollary 40. The following partial orders are countably universal (we take the ordering
![]() $\leq _{{\textsf {CT}}^-}$
on
$\leq _{{\textsf {CT}}^-}$
on
![]() $\mathsf {Cons}$
to be inherited from the Lindenbaum Algebra of
$\mathsf {Cons}$
to be inherited from the Lindenbaum Algebra of
![]() ${\textsf {CT}}^-$
):
${\textsf {CT}}^-$
):
-
•
 $\langle \mathsf {Sch}_{{\textsf {PA}}}^-, \leq _{{\textsf {CT}}^-}\rangle $
.
$\langle \mathsf {Sch}_{{\textsf {PA}}}^-, \leq _{{\textsf {CT}}^-}\rangle $
. -
•
 $\langle \mathsf {Sch}^T_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
.
$\langle \mathsf {Sch}^T_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
. -
•
 $\langle \mathsf {Cons}, \leq _{{\textsf {CT}}^-}\rangle .$
$\langle \mathsf {Cons}, \leq _{{\textsf {CT}}^-}\rangle .$
Proof This follows since
![]() $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
can be easily embedded into each of the above partial orders.
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
can be easily embedded into each of the above partial orders.
4 Prudently correct axiomatizations
Recall (from Definition 17) that
![]() $\Delta $
is the collection of prudent axiomatizations of
$\Delta $
is the collection of prudent axiomatizations of
![]() ${\textsf {PA}}$
. In the first subsection we classify the extensions of
${\textsf {PA}}$
. In the first subsection we classify the extensions of
![]() ${\textsf {PA}}$
that can be axiomatized by theories of the form
${\textsf {PA}}$
that can be axiomatized by theories of the form
![]() and measure the complexity of the Tarski Boundary problem for such theories.
and measure the complexity of the Tarski Boundary problem for such theories.
4.1 Universality and complexity
As indicated by the proposition below, theories of the form
![]() for
for
![]() $\delta \in \Delta $
are never too strong.
$\delta \in \Delta $
are never too strong.
Proposition 41. For every
![]() $\delta \in \Delta $
,
$\delta \in \Delta $
,
![]() .
.
Proof This follows immediately from Theorem 6 that
![]() ${\textsf {CT}}_0\vdash \forall \varphi \bigl ({\textsf {Pr}}_{{\textsf {PA}}}(\varphi )\rightarrow T(\varphi )\bigr )$
.
${\textsf {CT}}_0\vdash \forall \varphi \bigl ({\textsf {Pr}}_{{\textsf {PA}}}(\varphi )\rightarrow T(\varphi )\bigr )$
.
Therefore, the theory
![]() ${\textsf {CT}}_0$
provides an upper-bound for the strength of theories in question. The following theorem is this section’s main result.
${\textsf {CT}}_0$
provides an upper-bound for the strength of theories in question. The following theorem is this section’s main result.
Theorem 42. For any r.e.
![]() $\mathcal {L}_{{\textsf {PA}}}$
-theory
$\mathcal {L}_{{\textsf {PA}}}$
-theory
![]() $\mathcal {T}$
extending
$\mathcal {T}$
extending
![]() ${\textsf {PA}}$
such that
${\textsf {PA}}$
such that
![]() ${\textsf {CT}}_0\vdash \mathcal {T}$
there exists a
${\textsf {CT}}_0\vdash \mathcal {T}$
there exists a
![]() $\delta \in \Delta $
such that
$\delta \in \Delta $
such that
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() have the same arithmetical theorems.
have the same arithmetical theorems.
Proposition 41 and Theorem 42 when put together, yield the following characterization of arithmetical theories provable in
![]() $\text {REF}^{<\omega }({\textsf {PA}})$
.
$\text {REF}^{<\omega }({\textsf {PA}})$
.
Corollary 43. For every arithmetical recursively enumerable theory
![]() $\mathcal {T}$
extending
$\mathcal {T}$
extending
![]() ${\textsf {PA}}$
the following are equivalent:
${\textsf {PA}}$
the following are equivalent:
-
1.
 $\mathsf {REF}^{<\omega }({\textsf {PA}})\vdash \mathcal {T.}$
$\mathsf {REF}^{<\omega }({\textsf {PA}})\vdash \mathcal {T.}$
-
2. There exists a
 $\delta \in \Delta $
such that
$\delta \in \Delta $
such that
 $\mathcal {T}$
and
$\mathcal {T}$
and
 coincide on arithmetical theorems.
coincide on arithmetical theorems.
To prove Theorem 42 we need to arrange
![]() $\delta $
such that
$\delta $
such that
-
•
 $\delta \in \Delta $
.
$\delta \in \Delta $
. -
•
 does not overgenerate, i.e., its arithmetical consequences do not transcend those of
does not overgenerate, i.e., its arithmetical consequences do not transcend those of
 $\mathcal {T}$
.
$\mathcal {T}$
.
To satisfy the first condition we recall that by (Cieśliński’s) Theorem 6, uniform reflection over logic is an example of a principle which is provable in
![]() ${\textsf {PA}}$
and whose “globalized” version is equivalent to
${\textsf {PA}}$
and whose “globalized” version is equivalent to
![]() ${\textsf {CT}}_0$
. We shall often use the notation described in the following definition. We recall that, for heuristic reasons, we sometimes write
${\textsf {CT}}_0$
. We shall often use the notation described in the following definition. We recall that, for heuristic reasons, we sometimes write
![]() $\ulcorner \varphi \urcorner $
to denote either the Gödel number of
$\ulcorner \varphi \urcorner $
to denote either the Gödel number of
![]() $\varphi $
or the numeral naming this number (depending on the context).
$\varphi $
or the numeral naming this number (depending on the context).
Definition 44. For two sentences
![]() $\theta $
and
$\theta $
and
![]() $\varphi $
,
$\varphi $
,
![]() $\sigma _{\varphi }[\theta ]$
abbreviates the sentence
$\sigma _{\varphi }[\theta ]$
abbreviates the sentence
The map
![]() $\langle \varphi , \theta \rangle \mapsto \sigma _{\varphi }[\theta ]$
is clearly elementary and we shall identify it with its elementary definition.
$\langle \varphi , \theta \rangle \mapsto \sigma _{\varphi }[\theta ]$
is clearly elementary and we shall identify it with its elementary definition.
To satisfy the second condition we could use Vaught’s theorem on axiomatizability by a scheme, as we did earlier (see Remark 14). However, we prefer to introduce an original method of finding “deductively weak” axiomatizations of arithmetical theories. The very essence of our method was noted already in the original KKL-paper [Reference Kotlarski, Krajewski and Lachlan14]: there are models of
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
in which nonstandard pleonastic disjunctions of obviously false statements are deemed true by the truth predicate. For example, if
${\textsf {CT}}^-[{\textsf {PA}}]$
in which nonstandard pleonastic disjunctions of obviously false statements are deemed true by the truth predicate. For example, if
![]() $\mathcal {M}$
is a countable recursively saturated model of
$\mathcal {M}$
is a countable recursively saturated model of
![]() ${\textsf {PA}}$
and a is any nonstandard element, then there is a truth class
${\textsf {PA}}$
and a is any nonstandard element, then there is a truth class
![]() $T\subseteq M$
such that
$T\subseteq M$
such that
![]() $(\mathcal {M},T)\models {\textsf {CT}}^-[{\textsf {PA}}]$
and the sentence
$(\mathcal {M},T)\models {\textsf {CT}}^-[{\textsf {PA}}]$
and the sentence
 $$\begin{align*}\underbrace{0\neq 0 \vee (0\neq 0\vee (\ldots \vee 0\neq 0)\ldots )}_{a \text{ many disjuncts}}\end{align*}$$
$$\begin{align*}\underbrace{0\neq 0 \vee (0\neq 0\vee (\ldots \vee 0\neq 0)\ldots )}_{a \text{ many disjuncts}}\end{align*}$$
is deemed true by T. This phenomenon was quite recently pushed to the extreme by the following result of Bartosz Wcisło that appears in [Reference Cieśliński, Łełyk and Wcisło4].
Theorem 45. If
![]() $\mathcal {M}\models {\textsf {EA}}$
, then there is an elementary extension
$\mathcal {M}\models {\textsf {EA}}$
, then there is an elementary extension
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {M}$
that has an expansion
$\mathcal {M}$
that has an expansion
![]() $(\mathcal {N},T)\models {\textsf {CT}}^-[{\textsf {EA}}]$
, which has the property that every disjunction of nonstandard length in
$(\mathcal {N},T)\models {\textsf {CT}}^-[{\textsf {EA}}]$
, which has the property that every disjunction of nonstandard length in
![]() $\mathcal {N}$
is deemed true by T. Moreover, if
$\mathcal {N}$
is deemed true by T. Moreover, if
![]() $\mathcal {M}\models {\textsf {PA}}$
, then
$\mathcal {M}\models {\textsf {PA}}$
, then
![]() $(\mathcal {N},T)$
can be taken to be a model of
$(\mathcal {N},T)$
can be taken to be a model of
![]() .
.
The above theorem provides us with a new method of finding finite conservative axiomatizations of arithmetical theories extending
![]() ${\textsf {EA}}$
.
${\textsf {EA}}$
.
Definition 46. Given an arithmetical sentence
![]() $\varphi $
, the pleonastic disjunction of
$\varphi $
, the pleonastic disjunction of
![]() $\varphi $
is the sentence
$\varphi $
is the sentence
 $$\begin{align*}\underbrace{\varphi \vee (\varphi \vee (\ldots \vee \varphi)\ldots)}_{\ulcorner \varphi \urcorner \text{ times}}.\end{align*}$$
$$\begin{align*}\underbrace{\varphi \vee (\varphi \vee (\ldots \vee \varphi)\ldots)}_{\ulcorner \varphi \urcorner \text{ times}}.\end{align*}$$
The pleonastic disjunction of
![]() $\varphi $
will be denoted with
$\varphi $
will be denoted with
![]() $\bigvee \varphi $
.
$\bigvee \varphi $
.
Note that the above definition formalizes smoothly in
![]() ${\textsf {EA}}$
(in which case
${\textsf {EA}}$
(in which case
![]() $\varphi $
is identified with
$\varphi $
is identified with
![]() $\ulcorner \varphi \urcorner $
and treated both as a number and as a formula) and that in a nonstandard model of this theory
$\ulcorner \varphi \urcorner $
and treated both as a number and as a formula) and that in a nonstandard model of this theory
![]() $\bigvee \varphi $
has standard length if and only if
$\bigvee \varphi $
has standard length if and only if
![]() $\varphi $
is (coded by) a standard number.
$\varphi $
is (coded by) a standard number.
Proposition 47. Every r.e.
![]() $\mathcal {T}\supseteq {\textsf {EA}}$
can be finitely axiomatized by a theory of the form
$\mathcal {T}\supseteq {\textsf {EA}}$
can be finitely axiomatized by a theory of the form
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + T[\varphi ]$
, for some elementary formula
${\textsf {CT}}^-[{\textsf {EA}}] + T[\varphi ]$
, for some elementary formula
![]() $\varphi (x)$
.
$\varphi (x)$
.
We recall that, by our conventions,
![]() ${\textsf {CT}}^-[{\textsf {EA}}] + T[\varphi ]$
and
${\textsf {CT}}^-[{\textsf {EA}}] + T[\varphi ]$
and
![]() mean the same thing.
mean the same thing.
Proof Let
![]() $\varphi '(x)$
formalize an elementary axiomatization of
$\varphi '(x)$
formalize an elementary axiomatization of
![]() $\mathcal {T}$
(which exists by Craig’s trick). Define
$\mathcal {T}$
(which exists by Craig’s trick). Define
That is to say that x satisfies
![]() $\varphi $
if it is a pleonastic disjunction of a formula from an elementary axiomatization of
$\varphi $
if it is a pleonastic disjunction of a formula from an elementary axiomatization of
![]() $\mathcal {T}$
. Observe first that
$\mathcal {T}$
. Observe first that
. Indeed, it is sufficient to show that for every sentence
![]() $\psi $
we have
$\psi $
we have
Observe that, over
![]() ${\textsf {EA}}$
,
${\textsf {EA}}$
,
![]() $\varphi '(\psi )$
implies
$\varphi '(\psi )$
implies
![]() $\varphi (\bigvee \psi )$
, which in turn, over
$\varphi (\bigvee \psi )$
, which in turn, over
implies
![]() $T(\bigvee \psi )$
. However, over pure
$T(\bigvee \psi )$
. However, over pure
![]() ${\textsf {CT}}^-[{\textsf {EA}}]$
the last sentence implies
${\textsf {CT}}^-[{\textsf {EA}}]$
the last sentence implies
![]() $T(\psi )$
by compositional conditions, since
$T(\psi )$
by compositional conditions, since
![]() $\bigvee \psi $
is a disjunction of length
$\bigvee \psi $
is a disjunction of length
![]() $\ulcorner \psi \urcorner $
and hence is standard.
$\ulcorner \psi \urcorner $
and hence is standard.
We show conservativity: pick any model
![]() $\mathcal {M}\models \mathcal {T}$
. By Theorem 45 there is a
$\mathcal {M}\models \mathcal {T}$
. By Theorem 45 there is a
![]() $(\mathcal {N},T)\models {\textsf {CT}}^-[{\textsf {EA}}]$
such that
$(\mathcal {N},T)\models {\textsf {CT}}^-[{\textsf {EA}}]$
such that
![]() $\mathcal {N}$
is an elementary extension of
$\mathcal {N}$
is an elementary extension of
![]() $\mathcal {M}$
and every disjunction of nonstandard length is made true by T. It follows that
$\mathcal {M}$
and every disjunction of nonstandard length is made true by T. It follows that
![]() . Indeed, firstly observe that if
. Indeed, firstly observe that if
![]() $\mathcal {N}\models \varphi (a)$
then there exists
$\mathcal {N}\models \varphi (a)$
then there exists
![]() $\psi $
such that
$\psi $
such that
![]() $\mathcal {N}\models \varphi '(\psi ) \wedge a = \bigvee \psi $
. Now the argument splits into two cases:
$\mathcal {N}\models \varphi '(\psi ) \wedge a = \bigvee \psi $
. Now the argument splits into two cases:
-
1.
 $\psi $
is a standard sentence. In this case
$\psi $
is a standard sentence. In this case
 $\bigvee \psi $
is standard and
$\bigvee \psi $
is standard and
 $\mathcal {N}\models \bigvee \psi $
, by elementarity. Consequently
$\mathcal {N}\models \bigvee \psi $
, by elementarity. Consequently
 $(\mathcal {N}, T)\models T(\bigvee \psi )$
by compositional clauses; or
$(\mathcal {N}, T)\models T(\bigvee \psi )$
by compositional clauses; or -
2.
 $\psi $
is not a standard sentence. In this case
$\psi $
is not a standard sentence. In this case
 $\bigvee \psi $
is a disjunction of nonstandard length, hence is made true in
$\bigvee \psi $
is a disjunction of nonstandard length, hence is made true in
 $(\mathcal {N}, T)$
.
$(\mathcal {N}, T)$
.
We shall recycle the above conservativity argument in the proof of Theorem 42, which we now turn to.
Proof of Theorem 42
Fix
![]() $\mathcal {T}$
such that
$\mathcal {T}$
such that
Let
![]() $\varrho $
be an arbitrary elementary axiomatization of
$\varrho $
be an arbitrary elementary axiomatization of
![]() $\mathcal {T}$
. Let
$\mathcal {T}$
. Let
![]() $\sigma _{\varphi }[\theta ]$
denote the map from Definition 44. We now observe that the proof of the reflexive property of
$\sigma _{\varphi }[\theta ]$
denote the map from Definition 44. We now observe that the proof of the reflexive property of
![]() ${\textsf {PA}}$
is formalizable in I
${\textsf {PA}}$
is formalizable in I
![]() $\Sigma _1$
. This follows from two well-known facts: firstly, the cut-elimination theorem formalizes in I
$\Sigma _1$
. This follows from two well-known facts: firstly, the cut-elimination theorem formalizes in I
![]() $\Sigma _1$
(thus provably in I
$\Sigma _1$
(thus provably in I
![]() $\Sigma _1$
, every provable sentence has a proof that has the subformula property) and secondly, I
$\Sigma _1$
, every provable sentence has a proof that has the subformula property) and secondly, I
![]() $\Sigma _1$
is enough for the formalization of the proof of existence of partial truth predicates in
$\Sigma _1$
is enough for the formalization of the proof of existence of partial truth predicates in
![]() ${\textsf {PA}}$
. As a consequence, we obtain
${\textsf {PA}}$
. As a consequence, we obtain
Hence
![]() $\delta (x)\in \Delta $
, where
$\delta (x)\in \Delta $
, where
![]() $\delta $
is defined as follows:
$\delta $
is defined as follows:
Observe that
![]() $\delta $
naturally defines the following set of sentences:
$\delta $
naturally defines the following set of sentences:
We argue first that
is conservative over
![]() $\mathcal {T}$
. To see this, fix an arbitrary model
$\mathcal {T}$
. To see this, fix an arbitrary model
![]() $\mathcal {M}\models \mathcal {T}$
and let
$\mathcal {M}\models \mathcal {T}$
and let
be a model from Theorem 45. Then
since, reasoning by cases as in the proof of Proposition 47, for every
![]() $\varphi \in N$
such that
$\varphi \in N$
such that
![]() $\mathcal {N}\models \varrho (\varphi )$
we have
$\mathcal {N}\models \varrho (\varphi )$
we have
Now, we argue that
. Let
![]() $\varphi $
be an arbitrary
$\varphi $
be an arbitrary
![]() $\varrho $
–axiom of
$\varrho $
–axiom of
![]() $\mathcal {T}$
. We claim
$\mathcal {T}$
. We claim
To see why the last claim holds, reason in
. We have
By the axioms of
![]() ${\textsf {CT}}^-$
the above is equivalent to
${\textsf {CT}}^-$
the above is equivalent to
Now we reason by cases: either
![]() $\forall \theta ~ \bigl ({\textsf {Pr}}_{\emptyset }(\ulcorner \theta \urcorner )\rightarrow T(\theta )\bigr )$
or not. If the latter holds, we have
$\forall \theta ~ \bigl ({\textsf {Pr}}_{\emptyset }(\ulcorner \theta \urcorner )\rightarrow T(\theta )\bigr )$
or not. If the latter holds, we have
![]() $T(\bigvee \varphi )$
by Modus Ponens applied to (*). Hence
$T(\bigvee \varphi )$
by Modus Ponens applied to (*). Hence
![]() $\varphi $
holds by compositional conditions, because
$\varphi $
holds by compositional conditions, because
![]() $\bigvee \varphi $
is a disjunction of standard length and
$\bigvee \varphi $
is a disjunction of standard length and
![]() $\varphi $
is a standard sentence. If the former holds, we have
$\varphi $
is a standard sentence. If the former holds, we have
![]() ${\textsf {CT}}_0$
by Theorem 6 and
${\textsf {CT}}_0$
by Theorem 6 and
![]() $\varphi $
holds, because we assumed that
$\varphi $
holds, because we assumed that
![]() ${\textsf {CT}}_0\vdash \mathcal {T}$
.
${\textsf {CT}}_0\vdash \mathcal {T}$
.
We conclude this subsection with complexity results that complement Theorem 26.
Proposition 48. The set
![]() $\Delta ^*$
is
$\Delta ^*$
is
![]() $\Pi _2$
-complete.
$\Pi _2$
-complete.
Proof Clearly
![]() $\Delta ^*$
is
$\Delta ^*$
is
![]() $\Pi _2$
-definable. Consider the map f that takes a scheme template
$\Pi _2$
-definable. Consider the map f that takes a scheme template
![]() $\tau $
as input and outputs the formula
$\tau $
as input and outputs the formula
![]() $\delta _{\tau }(x)$
that expresses “x is an instance of
$\delta _{\tau }(x)$
that expresses “x is an instance of
![]() $\tau $
.” f is clearly recursive (indeed elementary) and satisfies
$\tau $
.” f is clearly recursive (indeed elementary) and satisfies
Therefore
![]() $\mathsf {Sch}_{{\textsf {PA}}}$
is many-one reducible to
$\mathsf {Sch}_{{\textsf {PA}}}$
is many-one reducible to
![]() $\Delta ^*$
, which in light of the
$\Delta ^*$
, which in light of the
![]() $\Pi _2$
-completeness of
$\Pi _2$
-completeness of
![]() $\mathsf {Sch}_{{\textsf {PA}}}$
(established in Theorem 26), completes the verification of
$\mathsf {Sch}_{{\textsf {PA}}}$
(established in Theorem 26), completes the verification of
![]() $\Pi _2$
-completeness of
$\Pi _2$
-completeness of
![]() $\Delta ^*$
.
$\Delta ^*$
.
Proposition 49. The sets
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta ^-$
are both
$\Delta ^-$
are both
![]() $\Sigma _1$
-complete.
$\Sigma _1$
-complete.
Proof Both sets are clearly r.e., because both definitions require just the provability of a particular sentence in I
![]() $\Sigma _1$
. To verify completeness we sketch the reduction f of the set of true
$\Sigma _1$
. To verify completeness we sketch the reduction f of the set of true
![]() $\Sigma _1$
-sentences to
$\Sigma _1$
-sentences to
![]() $\Delta $
(an analogous reduction works for
$\Delta $
(an analogous reduction works for
![]() $\Delta ^-$
). Given a
$\Delta ^-$
). Given a
![]() $\Sigma _1$
-sentence
$\Sigma _1$
-sentence
![]() $\varphi $
we define a formula
$\varphi $
we define a formula
![]() $f(\varphi ):= \delta _{{\textsf {PA}}}(x)\vee x = \varphi $
. It follows that
$f(\varphi ):= \delta _{{\textsf {PA}}}(x)\vee x = \varphi $
. It follows that
The left-to-right direction follows by I
![]() $\Sigma _1$
-provable
$\Sigma _1$
-provable
![]() $\Sigma _1$
-completeness of
$\Sigma _1$
-completeness of
![]() ${\textsf {PA}}$
. The right-to-left direction follows by the soundness of I
${\textsf {PA}}$
. The right-to-left direction follows by the soundness of I
![]() $\Sigma _1$
and
$\Sigma _1$
and
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
Theorem 50. The set
![]() $\left \{\delta \in \Delta \ \ | \ \ T[\delta ] \in \mathsf {Cons} \right \}$
is
$\left \{\delta \in \Delta \ \ | \ \ T[\delta ] \in \mathsf {Cons} \right \}$
is
![]() $\Pi _2$
-complete.
$\Pi _2$
-complete.
In what follows,
![]() $\Pi _2\text{-}\mathsf {REF}({\textsf {PA}})$
denotes the extension of
$\Pi _2\text{-}\mathsf {REF}({\textsf {PA}})$
denotes the extension of
![]() ${\textsf {EA}}$
with all sentences of the form
${\textsf {EA}}$
with all sentences of the form
for
![]() $\varphi (x)\in \Pi _2$
. It is a folklore result [Reference Beklemishev1] that this theory is finitely axiomatizable. We need the following folklore lemma, proved, e.g., in [Reference Pakhomov and Walsh23]:
$\varphi (x)\in \Pi _2$
. It is a folklore result [Reference Beklemishev1] that this theory is finitely axiomatizable. We need the following folklore lemma, proved, e.g., in [Reference Pakhomov and Walsh23]:
Lemma 51.
![]() ${\textsf {PA}}+ \neg \Pi _2\text{-}\mathrm{REF}({\textsf {PA}})$
is
${\textsf {PA}}+ \neg \Pi _2\text{-}\mathrm{REF}({\textsf {PA}})$
is
![]() $\Pi _2$
-sound.
$\Pi _2$
-sound.
Proof of Theorem 50
Fix a
![]() $\Pi _2$
-sentence
$\Pi _2$
-sentence
![]() $\pi := \forall x \varphi (x)$
, where
$\pi := \forall x \varphi (x)$
, where
![]() $\varphi (x)$
is
$\varphi (x)$
is
![]() $\Sigma _1$
. Let
$\Sigma _1$
. Let
![]() $\delta ^{\pi }$
be the formula in
$\delta ^{\pi }$
be the formula in
![]() $\Delta $
that describes the union of (the canonical axiomatization of)
$\Delta $
that describes the union of (the canonical axiomatization of)
![]() ${\textsf {PA}}$
with the following set of sentences:
${\textsf {PA}}$
with the following set of sentences:
The function
![]() $\pi \mapsto \delta ^{\pi }$
is clearly recursive, and
$\pi \mapsto \delta ^{\pi }$
is clearly recursive, and
![]() $\delta ^{\pi } \in \Delta $
. Let
$\delta ^{\pi } \in \Delta $
. Let
![]() $\theta (x):= \Pi _2\text{-}\text {REF}({\textsf {PA}})\vee \varphi (x)$
and observe that for every n,
$\theta (x):= \Pi _2\text{-}\text {REF}({\textsf {PA}})\vee \varphi (x)$
and observe that for every n,
![]() . Indeed, work in
. Indeed, work in
![]() and assume
and assume
![]() $\neg \Pi _2\text{-}\text {REF}({\textsf {PA}})$
. Then clearly
$\neg \Pi _2\text{-}\text {REF}({\textsf {PA}})$
. Then clearly
![]() $\neg {\textsf {CT}}_0$
and consequently, as in the proof of Theorem 42 we get
$\neg {\textsf {CT}}_0$
and consequently, as in the proof of Theorem 42 we get
![]() $T\left (\bigvee \varphi (\underline {n})\right )$
. Finally, the latter implies
$T\left (\bigvee \varphi (\underline {n})\right )$
. Finally, the latter implies
![]() $\varphi (\underline {n})$
, since it is a standard sentence.
$\varphi (\underline {n})$
, since it is a standard sentence.
Let
![]() $\mathsf {True}^{\mathbb {N}}_{\Pi _2}$
be the set of
$\mathsf {True}^{\mathbb {N}}_{\Pi _2}$
be the set of
![]() $\Pi _2$
-statements that are true in
$\Pi _2$
-statements that are true in
![]() $\mathbb {N}$
. We will prove
$\mathbb {N}$
. We will prove
Assume first that
![]() $\pi \in \mathsf {True}^{\mathbb {N}}_{\Pi _2}$
and
$\pi \in \mathsf {True}^{\mathbb {N}}_{\Pi _2}$
and
![]() $\pi = \forall x ~\varphi (x)$
, for some
$\pi = \forall x ~\varphi (x)$
, for some
![]() $\varphi (x)\in \Sigma _1$
. In particular
$\varphi (x)\in \Sigma _1$
. In particular
![]() $\varphi (\underline {n})$
is a true
$\varphi (\underline {n})$
is a true
![]() $\Sigma _1$
sentence for every
$\Sigma _1$
sentence for every
![]() $n \in \omega $
, hence,
$n \in \omega $
, hence,
As usual, fix any model
![]() $\mathcal {M}\models {\textsf {PA}}$
and take its elementary extension
$\mathcal {M}\models {\textsf {PA}}$
and take its elementary extension
in which every disjunction of nonstandard length is true. As previously, it follows that
.
Conversely, assume that
![]() is conservative over
is conservative over
![]() ${\textsf {PA}}$
. Then for every
${\textsf {PA}}$
. Then for every
![]() $n \in \omega $
,
$n \in \omega $
,
![]() ${\textsf {PA}}\vdash \theta (\underline {n})$
. In particular, for every
${\textsf {PA}}\vdash \theta (\underline {n})$
. In particular, for every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() ${\textsf {PA}}+\neg \Pi _2\text{-}\text {REF}({\textsf {PA}})\vdash \varphi (\underline {n})$
. By the soundness of this theory we conclude that
${\textsf {PA}}+\neg \Pi _2\text{-}\text {REF}({\textsf {PA}})\vdash \varphi (\underline {n})$
. By the soundness of this theory we conclude that
![]() $\pi $
is true.
$\pi $
is true.
4.2 Structure of prudent axiomatizations
Theorem 42 allows us to transfer results about the fragment of the Lindenbaum algebra of
![]() ${\textsf {PA}}$
consisting of sentences provable in
${\textsf {PA}}$
consisting of sentences provable in
![]() ${\textsf {CT}}_0$
to results about the structure of Tarski Boundary. Let us isolate the former structure: put
${\textsf {CT}}_0$
to results about the structure of Tarski Boundary. Let us isolate the former structure: put
where
![]() $[\varphi ]_{{\textsf {PA}}}$
denotes
$[\varphi ]_{{\textsf {PA}}}$
denotes
![]() $\varphi $
-equivalence class modulo
$\varphi $
-equivalence class modulo
![]() ${\textsf {PA}}$
-provable equivalence, i.e., the element of the Lindenbaum algebra of
${\textsf {PA}}$
-provable equivalence, i.e., the element of the Lindenbaum algebra of
![]() ${\textsf {PA}}$
that contains
${\textsf {PA}}$
that contains
![]() $\varphi $
. Then, it is fairly easy to see that the following holds:
$\varphi $
. Then, it is fairly easy to see that the following holds:
Observation 52.
![]() ${{\textsf {CT}}_0}/{{\textsf {PA}}}$
with the operations inherited from the Lindenbaum algebra of
${{\textsf {CT}}_0}/{{\textsf {PA}}}$
with the operations inherited from the Lindenbaum algebra of
![]() ${\textsf {PA}}$
is a lattice with a greatest but not a least element (obviously assuming the consistency of
${\textsf {PA}}$
is a lattice with a greatest but not a least element (obviously assuming the consistency of
![]() ${\textsf {CT}}_0$
). The lack of the least element follows from the fact that the arithmetical consequences of
${\textsf {CT}}_0$
). The lack of the least element follows from the fact that the arithmetical consequences of
![]() ${\textsf {CT}}_0$
is a theory in
${\textsf {CT}}_0$
is a theory in
![]() $\mathcal {L}_{{\textsf {PA}}}$
which extends
$\mathcal {L}_{{\textsf {PA}}}$
which extends
![]() ${\textsf {PA}}$
. In particular this theory is not finitely axiomatizable by essential reflexivity of
${\textsf {PA}}$
. In particular this theory is not finitely axiomatizable by essential reflexivity of
![]() ${\textsf {PA}}$
. Moreover the greatest element has no immediate predecessors. This follows by the classical fact that the Lindenbaum Algebra of
${\textsf {PA}}$
. Moreover the greatest element has no immediate predecessors. This follows by the classical fact that the Lindenbaum Algebra of
![]() ${\textsf {PA}}$
is dense (see [Reference Shavrukov and Visser27]) for a proof.
${\textsf {PA}}$
is dense (see [Reference Shavrukov and Visser27]) for a proof.
The following is an easy corollary to Theorem 42.
Proposition 53. There exists a lattice embedding
![]() ${{\textsf {CT}}_0}/{{\textsf {PA}}}\hookrightarrow \langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
.
${{\textsf {CT}}_0}/{{\textsf {PA}}}\hookrightarrow \langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
.
Proof To each
![]() $[\varphi ]_{{\textsf {PA}}}$
we assign
$[\varphi ]_{{\textsf {PA}}}$
we assign
![]() $\delta ^{\varphi } \in \Delta $
as in the proof of Theorem 42.
$\delta ^{\varphi } \in \Delta $
as in the proof of Theorem 42.
![]() $\varrho (x)$
is now simply
$\varrho (x)$
is now simply
![]() $x = \underline {\ulcorner \varphi \urcorner }$
. Hence by compositional axioms, and the fact that
$x = \underline {\ulcorner \varphi \urcorner }$
. Hence by compositional axioms, and the fact that
![]() $\varphi $
is standard we have
$\varphi $
is standard we have
Consequently,
![]() $\delta ^{\varphi }$
can be taken to axiomatize the (natural definition of the) following set of sentences:
$\delta ^{\varphi }$
can be taken to axiomatize the (natural definition of the) following set of sentences:
We claim that for an arbitrary
![]() $\varphi \in \mathcal {L}_{{\textsf {PA}}}$
, over
$\varphi \in \mathcal {L}_{{\textsf {PA}}}$
, over
![]() ,
,
![]() is equivalent to
is equivalent to
![]() $\varphi $
. Working in
$\varphi $
. Working in
![]() assume first that
assume first that
![]() $\varphi $
holds. Then for every
$\varphi $
holds. Then for every
![]() $\theta $
we have
$\theta $
we have
since
![]() $T(\sigma _{\varphi }[\theta ])$
is equivalent to an implication with a true conclusion. Hence every sentence satisfying
$T(\sigma _{\varphi }[\theta ])$
is equivalent to an implication with a true conclusion. Hence every sentence satisfying
![]() $\delta ^{\varphi }$
is true. For the converse implication, working over
$\delta ^{\varphi }$
is true. For the converse implication, working over
![]() , assume
, assume
![]() . We argue by cases:
. We argue by cases:
-
• If
 ${\textsf {CT}}_0$
holds, then
${\textsf {CT}}_0$
holds, then
 $\varphi $
holds, by assumption.
$\varphi $
holds, by assumption. -
• If
 ${\textsf {CT}}_0$
fails, then, as in the proof of Theorem 42,
${\textsf {CT}}_0$
fails, then, as in the proof of Theorem 42,
 $\varphi $
holds.
$\varphi $
holds.
We show that the mapping
![]() $\varphi \mapsto \delta ^{\varphi }$
is a lattice embedding. Firstly, we show that the mapping preserves the partial ordering. To this end, we prove that the following are equivalent for arbitrary arithmetical formulae
$\varphi \mapsto \delta ^{\varphi }$
is a lattice embedding. Firstly, we show that the mapping preserves the partial ordering. To this end, we prove that the following are equivalent for arbitrary arithmetical formulae
![]() $\varphi ,\psi $
that are provable in
$\varphi ,\psi $
that are provable in
![]() ${\textsf {CT}}_0$
:
${\textsf {CT}}_0$
:
-
•
 ${\textsf {PA}}\vdash \varphi \rightarrow \psi .$
${\textsf {PA}}\vdash \varphi \rightarrow \psi .$
-
•
 ${\textsf {CT}}^-[{\textsf {PA}}]\vdash T[\delta ^{\varphi }]\rightarrow T[\delta ^{\psi }].$
${\textsf {CT}}^-[{\textsf {PA}}]\vdash T[\delta ^{\varphi }]\rightarrow T[\delta ^{\psi }].$
Indeed the top-to-bottom direction follows easily, since for an arbitrary
![]() $\varphi \in \mathcal {L}_{{\textsf {PA}}}$
,
$\varphi \in \mathcal {L}_{{\textsf {PA}}}$
,
![]() is equivalent to
is equivalent to
![]() $\varphi $
and
$\varphi $
and
![]() proves
proves
![]() . The bottom-to-up direction uses the same observations plus additionally the conservativity of
. The bottom-to-up direction uses the same observations plus additionally the conservativity of
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
over
${\textsf {CT}}^-[{\textsf {PA}}]$
over
![]() ${\textsf {PA}}$
. Finally, we show that the mapping preserves infima and suprema. It is enough to observe that for
${\textsf {PA}}$
. Finally, we show that the mapping preserves infima and suprema. It is enough to observe that for
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
as above,
$\psi $
as above,
![]() is equivalent to
is equivalent to
![]() and the same with
and the same with
![]() $\wedge .$
This concludes the proof.
$\wedge .$
This concludes the proof.
The next proposition slightly lies on the margins of our considerations as it does not concern axiomatizations of
![]() ${\textsf {PA}}$
, but rather concerns the set of theorems of
${\textsf {PA}}$
, but rather concerns the set of theorems of
![]() ${\textsf {PA}}$
. However, we include it, since it reveals an interesting feature of the Tarski Boundary.
${\textsf {PA}}$
. However, we include it, since it reveals an interesting feature of the Tarski Boundary.
Proposition 54. There is an embedding
![]() $\iota : {{\textsf {CT}}_0}/{{\textsf {PA}}}\hookrightarrow \langle \Delta ^-, \leq _{{\textsf {CT}}^-}\rangle $
that is cofinal in the region below (i.e., the nonconservative side of) the Tarski Boundary. More precisely, for every
$\iota : {{\textsf {CT}}_0}/{{\textsf {PA}}}\hookrightarrow \langle \Delta ^-, \leq _{{\textsf {CT}}^-}\rangle $
that is cofinal in the region below (i.e., the nonconservative side of) the Tarski Boundary. More precisely, for every
![]() $\alpha \in \mathcal {L}_T$
such that
$\alpha \in \mathcal {L}_T$
such that
![]() ${\textsf {CT}}^-[{\textsf {PA}}] + \alpha $
is non-conservative over
${\textsf {CT}}^-[{\textsf {PA}}] + \alpha $
is non-conservative over
![]() ${\textsf {PA}}$
, there is an
${\textsf {PA}}$
, there is an
![]() $a\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
such that
$a\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
such that
![]() $T[\iota (a)]$
is strictly above
$T[\iota (a)]$
is strictly above
![]() $\alpha $
(i.e., is logically weaker) and
$\alpha $
(i.e., is logically weaker) and
![]() ${\textsf {CT}}^-[{\textsf {PA}}] + T[\iota (a)]$
is non-conservative over
${\textsf {CT}}^-[{\textsf {PA}}] + T[\iota (a)]$
is non-conservative over
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
Proof The embedding
![]() $\iota $
is defined as in the proof of the previous proposition with the only exception that we do not add
$\iota $
is defined as in the proof of the previous proposition with the only exception that we do not add
![]() ${\textsf {PA}}$
to
${\textsf {PA}}$
to
![]() $\delta ^{\psi }$
. More concretely, if
$\delta ^{\psi }$
. More concretely, if
![]() $[\varphi ]_{{\textsf {PA}}}\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
, then we put
$[\varphi ]_{{\textsf {PA}}}\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
, then we put
![]() $\iota ([\varphi ]_{{\textsf {PA}}})$
to be the natural elementary definition of the following set of sentences:
$\iota ([\varphi ]_{{\textsf {PA}}})$
to be the natural elementary definition of the following set of sentences:
Denote the canonical elementary definition of this set with
![]() $\delta ^{\varphi }$
. As in the proof of the previous proposition, we obtain that for every
$\delta ^{\varphi }$
. As in the proof of the previous proposition, we obtain that for every
![]() $[\varphi ]_{{\textsf {PA}}}\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
, provably in
$[\varphi ]_{{\textsf {PA}}}\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
, provably in
![]() ${\textsf {CT}}^-[{\textsf {PA}}]$
,
${\textsf {CT}}^-[{\textsf {PA}}]$
,
![]() $\varphi $
is equivalent to
$\varphi $
is equivalent to
![]() $T[\delta ^{\varphi }]$
. Consequently,
$T[\delta ^{\varphi }]$
. Consequently,
![]() $\iota $
is a lattice embedding. Now we claim that
$\iota $
is a lattice embedding. Now we claim that
![]() $\iota $
is cofinal with the Tarski Boundary in the sense explained. Pick any
$\iota $
is cofinal with the Tarski Boundary in the sense explained. Pick any
![]() $\alpha \in \mathcal {L}_{T}$
such that
$\alpha \in \mathcal {L}_{T}$
such that
![]() ${\textsf {CT}}^-[{\textsf {PA}}] + \alpha $
is non-conservative over
${\textsf {CT}}^-[{\textsf {PA}}] + \alpha $
is non-conservative over
![]() ${\textsf {PA}}$
(but consistent). By definition,
${\textsf {PA}}$
(but consistent). By definition,
![]() ${\textsf {CT}}^-[{\textsf {PA}}]+\alpha \vdash \varphi $
for some
${\textsf {CT}}^-[{\textsf {PA}}]+\alpha \vdash \varphi $
for some
![]() ${\textsf {PA}}$
- unprovable sentence
${\textsf {PA}}$
- unprovable sentence
![]() $\varphi \in \mathcal {L}_{{\textsf {PA}}}$
. Then, since the Lindenbaum algebra of
$\varphi \in \mathcal {L}_{{\textsf {PA}}}$
. Then, since the Lindenbaum algebra of
![]() ${\textsf {PA}}$
is atomless there is a sentence
${\textsf {PA}}$
is atomless there is a sentence
![]() $\psi \in \mathcal {L}_{{\textsf {PA}}}$
, which is logically strictly weaker than
$\psi \in \mathcal {L}_{{\textsf {PA}}}$
, which is logically strictly weaker than
![]() $\varphi $
. Then there is a sentence
$\varphi $
. Then there is a sentence
![]() $\theta $
such that
$\theta $
such that
![]() $[\theta ]_{{\textsf {PA}}}\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
and
$[\theta ]_{{\textsf {PA}}}\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
and
![]() $\psi \vee \theta $
is unprovable in
$\psi \vee \theta $
is unprovable in
![]() ${\textsf {PA}}$
. This holds, since it is known that over
${\textsf {PA}}$
. This holds, since it is known that over
![]() ${\textsf {PA}}$
,
${\textsf {PA}}$
,
![]() $\mathsf {REF}({\textsf {PA}})$
(which is a consequence of
$\mathsf {REF}({\textsf {PA}})$
(which is a consequence of
![]() ${\textsf {CT}}_0$
) does not follow from any finite, consistent, set of sentences. Hence
${\textsf {CT}}_0$
) does not follow from any finite, consistent, set of sentences. Hence
![]() $[\psi \vee \theta ]_{{\textsf {PA}}}\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
is not the greatest element. Consequently,
$[\psi \vee \theta ]_{{\textsf {PA}}}\in {{\textsf {CT}}_0}/{{\textsf {PA}}}$
is not the greatest element. Consequently,
![]() $T[\iota (\psi \vee \theta )] = T[\delta ^{\psi \vee \theta }]$
is below the Tarski Boundary. However, since
$T[\iota (\psi \vee \theta )] = T[\delta ^{\psi \vee \theta }]$
is below the Tarski Boundary. However, since
![]() $\psi $
does not prove
$\psi $
does not prove
![]() $\varphi $
(over
$\varphi $
(over
![]() ${\textsf {PA}}$
), a fortiori
${\textsf {PA}}$
), a fortiori
![]() $\psi \vee \theta $
does not prove
$\psi \vee \theta $
does not prove
![]() $\varphi $
. Hence
$\varphi $
. Hence
![]() does not prove
does not prove
![]() ${\textsf {CT}}^-[{\textsf {PA}}]+\alpha $
. Additionally,
${\textsf {CT}}^-[{\textsf {PA}}]+\alpha $
. Additionally,
![]() , since
, since
![]() $\psi \vee \theta $
follows from
$\psi \vee \theta $
follows from
![]() $\alpha $
.
$\alpha $
.
Proposition 55. There are recursive infinite antichains in
![]() $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
.
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
.
Proof We shall make use of a
![]() $\Pi _1$
-formula that is
$\Pi _1$
-formula that is
![]() ${\textsf {PA}}$
-independent, i.e., for every binary sequence s of length
${\textsf {PA}}$
-independent, i.e., for every binary sequence s of length
![]() $n\in \omega $
the following sentence is unprovable in
$n\in \omega $
the following sentence is unprovable in
![]() ${\textsf {PA}}$
:
${\textsf {PA}}$
:
where for any formula
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi ^{0} := \varphi ,$
and
$\varphi ^{0} := \varphi ,$
and
![]() $\varphi ^{1}:= \lnot \varphi $
. We will use the construction of such a
$\varphi ^{1}:= \lnot \varphi $
. We will use the construction of such a
![]() $\Pi _1$
-formula described in [Reference Lindström21, Theorem 9, Chapter 2]. Let
$\Pi _1$
-formula described in [Reference Lindström21, Theorem 9, Chapter 2]. Let
![]() $\pi (x)$
be such a formula. Assuming that each
$\pi (x)$
be such a formula. Assuming that each
![]() $\pi (\underline {k})$
is provable in
$\pi (\underline {k})$
is provable in
![]() ${\textsf {CT}}_0$
,
${\textsf {CT}}_0$
,
![]() $\{\pi (\underline {k})\}_{k\in \omega }$
is an infinite antichain in
$\{\pi (\underline {k})\}_{k\in \omega }$
is an infinite antichain in
![]() ${{\textsf {CT}}_0}/{{\textsf {PA}}}$
. By Proposition 53 this implies that
${{\textsf {CT}}_0}/{{\textsf {PA}}}$
. By Proposition 53 this implies that
![]() $\{\delta ^{\pi (\underline {k})}\}_{k\in \omega }$
is an infinite antichain in
$\{\delta ^{\pi (\underline {k})}\}_{k\in \omega }$
is an infinite antichain in
![]() $\Delta $
. These considerations show that it suffices to verify
$\Delta $
. These considerations show that it suffices to verify
The verification of
![]() $(*)$
is a straightforward formalization of the reasoning in [Reference Lindström21, Theorem 9, Chapter 2], so it is delegated to the Appendix.
$(*)$
is a straightforward formalization of the reasoning in [Reference Lindström21, Theorem 9, Chapter 2], so it is delegated to the Appendix.
Proposition 56. There is an embedding
![]() $(\mathbb {Q}, <) \hookrightarrow \langle \Delta , \leq _{{\textsf {CT}}^-}\rangle .$
$(\mathbb {Q}, <) \hookrightarrow \langle \Delta , \leq _{{\textsf {CT}}^-}\rangle .$
Proof This is an immediate consequence of the existence of an embedding
![]() $(\mathbb {Q}, <)\hookrightarrow {{\textsf {CT}}_0}/{{\textsf {PA}}}$
, which in turn follows from the well-known fact that the Lindenbaum Algebra of
$(\mathbb {Q}, <)\hookrightarrow {{\textsf {CT}}_0}/{{\textsf {PA}}}$
, which in turn follows from the well-known fact that the Lindenbaum Algebra of
![]() ${\textsf {PA}}$
is dense (see [Reference Shavrukov and Visser27] for a proof).
${\textsf {PA}}$
is dense (see [Reference Shavrukov and Visser27] for a proof).
Proposition 57. There are
![]() $\delta , \delta '\in \Delta $
such that
$\delta , \delta '\in \Delta $
such that
![]() and
and
![]() are non-conservative extensions of
are non-conservative extensions of
![]() ${\textsf {PA}}$
, but
${\textsf {PA}}$
, but
![]() is a conservative extension of
is a conservative extension of
![]() ${\textsf {PA}}$
.
${\textsf {PA}}$
.
Proof Consider
![]() $\varphi := {\textsf {Con}}_{{\textsf {PA}} + \neg {\textsf {Con}}_{{\textsf {PA}}}}$
and
$\varphi := {\textsf {Con}}_{{\textsf {PA}} + \neg {\textsf {Con}}_{{\textsf {PA}}}}$
and
![]() $\psi := {\textsf {Con}}_{{\textsf {PA}}}\rightarrow {\textsf {Con}}_{{\textsf {PA}}+{\textsf {Con}}_{{\textsf {PA}}}}$
. Both
$\psi := {\textsf {Con}}_{{\textsf {PA}}}\rightarrow {\textsf {Con}}_{{\textsf {PA}}+{\textsf {Con}}_{{\textsf {PA}}}}$
. Both
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
generate different non-zero elements in
$\psi $
generate different non-zero elements in
![]() ${{\textsf {CT}}_0}/{{\textsf {PA}}}$
but it is easy to see that
${{\textsf {CT}}_0}/{{\textsf {PA}}}$
but it is easy to see that
Hence the desired
![]() $\delta , \delta '\in \Delta $
can be chosen as
$\delta , \delta '\in \Delta $
can be chosen as
![]() $\delta :=\delta ^{\varphi }$
and
$\delta :=\delta ^{\varphi }$
and
![]() $\delta ':= \delta ^{\psi }$
(defined as in the proof of Proposition 53).
$\delta ':= \delta ^{\psi }$
(defined as in the proof of Proposition 53).
5 Coda: The arithmetical reach of
 for
for
 $\delta \in \Delta ^*$
$\delta \in \Delta ^*$
Recall from Definition 17 that
![]() $\Delta ^*$
is the collection of elementary presentations of
$\Delta ^*$
is the collection of elementary presentations of
![]() ${\textsf {PA}}$
, i.e., elementary formulae that define (in
${\textsf {PA}}$
, i.e., elementary formulae that define (in
![]() $\mathbb {N}$
) a theory that is deductively equivalent to
$\mathbb {N}$
) a theory that is deductively equivalent to
![]() ${\textsf {PA}}$
. We are now in a position to fulfill our promise given in the introduction and characterize the set denoted
${\textsf {PA}}$
. We are now in a position to fulfill our promise given in the introduction and characterize the set denoted
![]() $\sup {\textsf {PA}}$
of arithmetical sentences that are provable in some theory of the form
$\sup {\textsf {PA}}$
of arithmetical sentences that are provable in some theory of the form
![]() , where
, where
![]() $\delta \in \Delta ^*$
.
$\delta \in \Delta ^*$
.
Theorem 58.
![]() $\sup {\textsf {PA}}$
is deductively equivalent to
$\sup {\textsf {PA}}$
is deductively equivalent to
![]() $\mathsf {True}^{\mathbb {N}}_{\Pi _2} + \mathsf {REF}^{<\omega }({\textsf {PA}}).$
$\mathsf {True}^{\mathbb {N}}_{\Pi _2} + \mathsf {REF}^{<\omega }({\textsf {PA}}).$
Proof First note that
![]() $\mathsf {REF}^{<\omega }({\textsf {PA}})\subseteq \sup {\textsf {PA}}$
is an immediate corollary to Theorem 42. Also, the proof of
$\mathsf {REF}^{<\omega }({\textsf {PA}})\subseteq \sup {\textsf {PA}}$
is an immediate corollary to Theorem 42. Also, the proof of
![]() $\mathsf {True}^{\mathbb {N}}_{\Pi _2}\subseteq \sup {\textsf {PA}}$
is morally contained in the proof of Theorem 26: for every true
$\mathsf {True}^{\mathbb {N}}_{\Pi _2}\subseteq \sup {\textsf {PA}}$
is morally contained in the proof of Theorem 26: for every true
![]() $\Pi _2$
-sentence
$\Pi _2$
-sentence
![]() $\pi := \forall x \exists y \varphi (x,y)$
, the theory
$\pi := \forall x \exists y \varphi (x,y)$
, the theory
is deductively equivalent to
![]() ${\textsf {PA}}$
, hence the natural arithmetical definition of the above set witnesses that
${\textsf {PA}}$
, hence the natural arithmetical definition of the above set witnesses that
![]() $\sup {\textsf {PA}}\vdash \pi $
. To prove the converse inclusionFootnote
13
, assume that for some
$\sup {\textsf {PA}}\vdash \pi $
. To prove the converse inclusionFootnote
13
, assume that for some
![]() $\delta \in \Delta $
,
$\delta \in \Delta $
,
![]() . Let
. Let
![]() $\pi $
be the true
$\pi $
be the true
![]() $\Pi _2$
-sentence
$\Pi _2$
-sentence
expressing that every theorem of
![]() $\delta $
is provable already in
$\delta $
is provable already in
![]() ${\textsf {PA}}$
. Then it is easy to observe that
${\textsf {PA}}$
. Then it is easy to observe that
However, by any of the proofs of Theorem 5, the theory
![]() ${\textsf {CT}}^-[{\textsf {PA}}] + \pi + \mathsf {GRP}({\textsf {PA}})$
is arithmetically conservative over
${\textsf {CT}}^-[{\textsf {PA}}] + \pi + \mathsf {GRP}({\textsf {PA}})$
is arithmetically conservative over
![]() ${\textsf {EA}} + \mathsf {REF}^{<\omega }({\textsf {PA}}) + \pi $
.Footnote
14
Hence
${\textsf {EA}} + \mathsf {REF}^{<\omega }({\textsf {PA}}) + \pi $
.Footnote
14
Hence
![]() ${\textsf {EA}} + \mathsf {REF}^{<\omega }({\textsf {PA}}) + \pi \vdash \varphi $
. Since
${\textsf {EA}} + \mathsf {REF}^{<\omega }({\textsf {PA}}) + \pi \vdash \varphi $
. Since
![]() ${\textsf {EA}} + \pi $
is a true
${\textsf {EA}} + \pi $
is a true
![]() $\Pi _2$
-sentence the proof is complete.
$\Pi _2$
-sentence the proof is complete.
6 Open problems
-
(I) Are the lattices
 $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
 $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
dense? Does
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
dense? Does
 $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
have maximal or minimal elements? Does
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
have maximal or minimal elements? Does
 $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
have minimal elements (by the proof of Theorem 30 no
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
have minimal elements (by the proof of Theorem 30 no
 $\leq _{{\textsf {CT}}^-}$
-maximal element exists)?
$\leq _{{\textsf {CT}}^-}$
-maximal element exists)? -
(II) Are the lattices
 $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
 $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
universal for countable distributive lattices?Footnote
15
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
universal for countable distributive lattices?Footnote
15
-
(III) How do
 $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
 $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
fit in the Lindenbaum algebra of
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
fit in the Lindenbaum algebra of
 ${\textsf {CT}}^-[{\textsf {EA}}]$
?
${\textsf {CT}}^-[{\textsf {EA}}]$
? -
(IV) Is the Lindenbaum algebra of
 $\mathsf {Cons}$
dense?
$\mathsf {Cons}$
dense? -
(V) Do
 $\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
$\langle \mathsf {Sch}_{{\textsf {PA}}}, \leq _{{\textsf {CT}}^-}\rangle $
and
 $\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
have decidable copies? If not, how undecidable are they?
$\langle \Delta , \leq _{{\textsf {CT}}^-}\rangle $
have decidable copies? If not, how undecidable are they? -
(VI) How close can we get to the Tarski Boundary from below using theories
 , where
, where
 $\delta \in \Delta $
? In other words, if
$\delta \in \Delta $
? In other words, if
 ${\textsf {CT}}^-[{\textsf {PA}}] + \alpha $
is nonconservative over
${\textsf {CT}}^-[{\textsf {PA}}] + \alpha $
is nonconservative over
 ${\textsf {PA}}$
, is there some
${\textsf {PA}}$
, is there some
 $\delta \in \Delta $
such that
$\delta \in \Delta $
such that
 is nonconservative over PA, and
is nonconservative over PA, and
 ${\textsf {CT}}^-[{\textsf {PA}}] + \alpha \vdash T[\delta ]$
?
${\textsf {CT}}^-[{\textsf {PA}}] + \alpha \vdash T[\delta ]$
? -
(VII) How close can we get to the Tarski Boundary from above using theories
 , where
, where
 $\delta \in \Delta $
? In other words, if
$\delta \in \Delta $
? In other words, if
 ${\textsf {CT}}^-[{\textsf {PA}}] + \alpha $
is conservative over
${\textsf {CT}}^-[{\textsf {PA}}] + \alpha $
is conservative over
 ${\textsf {PA}}$
, is there some
${\textsf {PA}}$
, is there some
 $\delta \in \Delta $
such that
$\delta \in \Delta $
such that
 is conservative over PA, and
is conservative over PA, and
 ${\textsf {CT}}^-[{\textsf {PA}}] + T[\delta ] \vdash \alpha $
?
${\textsf {CT}}^-[{\textsf {PA}}] + T[\delta ] \vdash \alpha $
? -
(VIII) Do the answers to Questions (VI) and (VII) change if
 is required to be a subtheory of
is required to be a subtheory of
 ${\textsf {CT}}_0$
?
${\textsf {CT}}_0$
?
7 Appendix
Proof Verification of (*) of the proof of Proposition 55
To lighten the notation, we will identify numerals with their denotations, and formulae with their codes. We wish to show that if
![]() $\pi (x)$
is the
$\pi (x)$
is the
![]() $\Pi _1$
-formula
$\Pi _1$
-formula
![]() $\pi (x)$
constructed in [Reference Lindström21, Theorem 9, Chapter 2], then for every
$\pi (x)$
constructed in [Reference Lindström21, Theorem 9, Chapter 2], then for every
![]() $k\in \omega $
,
$k\in \omega $
,
![]() ${\textsf {CT}}_0\vdash \pi (k)$
. Let us revisit the construction of
${\textsf {CT}}_0\vdash \pi (k)$
. Let us revisit the construction of
![]() $\pi (x)$
. Given a finite binary sequence s of length n, and a unary arithmetical formula
$\pi (x)$
. Given a finite binary sequence s of length n, and a unary arithmetical formula
![]() $\varphi (x)$
, let
$\varphi (x)$
, let
![]() $\varphi ^s$
abbreviate the following sentence:
$\varphi ^s$
abbreviate the following sentence:
For a unary formula
![]() $\varphi $
, let
$\varphi $
, let
![]() $\varrho (x,i,\varphi ,p)$
express:
$\varrho (x,i,\varphi ,p)$
express:
Finally, let
![]() $\pi (x)$
be a formula assured to exist by the diagonal lemma such that the following is provable in
$\pi (x)$
be a formula assured to exist by the diagonal lemma such that the following is provable in
![]() ${\textsf {PA}}$
:
${\textsf {PA}}$
:
By metainduction on
![]() $n\in \omega $
, we show that for every
$n\in \omega $
, we show that for every
![]() $n \in \omega $
,
$n \in \omega $
,
![]() ${\textsf {CT}}_0\vdash \bigl ({\textsf {len}}(s) = n+1 \rightarrow \neg {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^s)\bigr ).$
Observe that this implies that for every
${\textsf {CT}}_0\vdash \bigl ({\textsf {len}}(s) = n+1 \rightarrow \neg {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^s)\bigr ).$
Observe that this implies that for every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\pi (n)$
is provable in
$\pi (n)$
is provable in
![]() ${\textsf {CT}}_0$
. We first show that
${\textsf {CT}}_0$
. We first show that
![]() $\pi (0)$
is provable in
$\pi (0)$
is provable in
![]() ${\textsf {CT}}_0$
. Working in
${\textsf {CT}}_0$
. Working in
![]() ${\textsf {CT}}_0$
, assume that
${\textsf {CT}}_0$
, assume that
![]() $\neg \pi (0)$
holds. It follows that for some p,
$\neg \pi (0)$
holds. It follows that for some p,
![]() $\varrho (0,1,\pi ,p)$
holds, hence in particular,
$\varrho (0,1,\pi ,p)$
holds, hence in particular,
![]() ${\textsf {Pr}}_{{\textsf {PA}}}(\pi (0))$
holds. However, in
${\textsf {Pr}}_{{\textsf {PA}}}(\pi (0))$
holds. However, in
![]() ${\textsf {CT}}_0$
the theorems of
${\textsf {CT}}_0$
the theorems of
![]() ${\textsf {PA}}$
are true, so
${\textsf {PA}}$
are true, so
![]() $\pi (0)$
holds, contrary to the assumption. Hence
$\pi (0)$
holds, contrary to the assumption. Hence
![]() ${\textsf {CT}}_0\vdash \neg {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi (0))$
. Moreover, since
${\textsf {CT}}_0\vdash \neg {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi (0))$
. Moreover, since
![]() $\pi (0)$
holds, for every
$\pi (0)$
holds, for every
![]() ${\textsf {PA}}$
-proof of
${\textsf {PA}}$
-proof of
![]() $\pi (0)$
there exists a smaller
$\pi (0)$
there exists a smaller
![]() ${\textsf {PA}}$
-proof of
${\textsf {PA}}$
-proof of
![]() $\neg \pi (0)$
. Consequently, since
$\neg \pi (0)$
. Consequently, since
![]() ${\textsf {CT}}_0$
proves the consistency of
${\textsf {CT}}_0$
proves the consistency of
![]() ${\textsf {PA}}$
, for
${\textsf {PA}}$
, for
![]() $n=0$
,
$n=0$
,
![]() ${\textsf {CT}}_0 \vdash \forall s \bigl ({\textsf {len}}(s) = n+1 \rightarrow \neg {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^s)\bigr )$
.
${\textsf {CT}}_0 \vdash \forall s \bigl ({\textsf {len}}(s) = n+1 \rightarrow \neg {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^s)\bigr )$
.
Now, assume
![]() $n = k+1$
,
$n = k+1$
,
![]() ${\textsf {CT}}_0\vdash \forall s \bigl ({\textsf {len}}(s) = n \rightarrow \neg {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^s)\bigr )$
. Working in
${\textsf {CT}}_0\vdash \forall s \bigl ({\textsf {len}}(s) = n \rightarrow \neg {\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^s)\bigr )$
. Working in
![]() ${\textsf {CT}}_0$
assume for some s of length
${\textsf {CT}}_0$
assume for some s of length
![]() $n+1$
,
$n+1$
,
![]() ${\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^s).$
Fix s such that the proof of
${\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^s).$
Fix s such that the proof of
![]() $\pi ^s$
in
$\pi ^s$
in
![]() ${\textsf {PA}}$
is the least possible (among s’s of length
${\textsf {PA}}$
is the least possible (among s’s of length
![]() $n+1$
). Denote (the code of) this proof with p. We distinguish two cases:
$n+1$
). Denote (the code of) this proof with p. We distinguish two cases:
-
1.
 $s(n) = 0$
. Then, by the definition of
$s(n) = 0$
. Then, by the definition of
 $\pi ^s$
, we have
$\pi ^s$
, we have
 ${\textsf {Pr}}_{{\textsf {PA}}}(\pi ^{s\upharpoonright _{n}}\rightarrow \neg \pi (n))$
. Moreover, both
${\textsf {Pr}}_{{\textsf {PA}}}(\pi ^{s\upharpoonright _{n}}\rightarrow \neg \pi (n))$
. Moreover, both
 $\varrho (n,0,\pi ,p)$
and
$\varrho (n,0,\pi ,p)$
and
 $\forall q\leq p~ \neg \varrho (n,1,\pi ,q)$
hold. Since
$\forall q\leq p~ \neg \varrho (n,1,\pi ,q)$
hold. Since
 $\varrho $
is a
$\varrho $
is a
 $\Delta _0$
-formula, we have
$\Delta _0$
-formula, we have  $$\begin{align*}{\textsf{Pr}}_{{\textsf{PA}}}\bigl(\varrho(n,0,\pi,p)\wedge \forall q\leq p~\neg\varrho(n,1,\pi,q)\bigr).\end{align*}$$
$$\begin{align*}{\textsf{Pr}}_{{\textsf{PA}}}\bigl(\varrho(n,0,\pi,p)\wedge \forall q\leq p~\neg\varrho(n,1,\pi,q)\bigr).\end{align*}$$
In particular,
 ${\textsf {Pr}}_{{\textsf {PA}}}(\pi (n))$
. Hence
${\textsf {Pr}}_{{\textsf {PA}}}(\pi (n))$
. Hence
 ${\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^{s\upharpoonright _{n}})$
, which is impossible by the induction step, since
${\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi ^{s\upharpoonright _{n}})$
, which is impossible by the induction step, since
 $s\!\upharpoonright _{n}$
has length n.
$s\!\upharpoonright _{n}$
has length n. -
2.
 $s(n) = 1$
. Then, as before,
$s(n) = 1$
. Then, as before,
 ${\textsf {Pr}}_{{\textsf {PA}}}(\pi ^{s\upharpoonright _{n}}\rightarrow \pi (n)).$
Moreover, by minimality of p, we have
${\textsf {Pr}}_{{\textsf {PA}}}(\pi ^{s\upharpoonright _{n}}\rightarrow \pi (n)).$
Moreover, by minimality of p, we have
 $\varrho (n,1,\pi ,p)$
and
$\varrho (n,1,\pi ,p)$
and
 $\forall q<p ~ \neg \varrho (n,0,\pi ,q)$
. Hence, as before we obtain
$\forall q<p ~ \neg \varrho (n,0,\pi ,q)$
. Hence, as before we obtain
 ${\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi (n))$
, which contradicts the induction assumption.
${\textsf {Pr}}_{{\textsf {PA}}}(\neg \pi (n))$
, which contradicts the induction assumption.
This concludes the proof of the induction step and the whole proof.
8 Acknowledgements
We have both directly and indirectly benefitted from conversations with several colleagues concerning the topics explored in this paper, including (in reverse alphabetical order of last names) Bartosz Wcisło, Albert Visser, Fedor Pakhomov, Carlo Nicolai, Roman Kossak, Cezary Cieśliński, Lev Beklemishev, and Athar Abdul-Quader. The research presented in this paper was supported by the National Science Centre, Poland (NCN; Grant Number 2019/34/A/HS1/00399).