Article contents
Arithmetical representation of recursively enumerable sets
Published online by Cambridge University Press: 12 March 2014
Extract
A set S of natural numbers is called recursively enumerable if there is a general recursive function F(x, y) such that
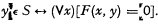
In other words, S is the projection of a two-dimensional general recursive set. Actually, it is no restriction on S to assume that F(x, y) is primitive recursive. If S is not empty, it is the range of the primitive recursive function
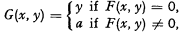
where a is a fixed element of S. Using pairing functions, we see that any non-empty recursively enumerable set is also the range of a primitive recursive function of one variable.
We use throughout the logical symbols ⋀ (and), ⋁ (or), → (if…then…), ↔ (if and only if), ∧ (for every), and ∨(there exists); negation does not occur explicitly. The variables range over the natural numbers, except as otherwise noted.
Martin Davis has shown that every recursively enumerable set S of natural numbers can be represented in the form
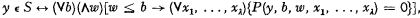
where P(y, b, w, x1 …, xλ) is a polynomial with integer coefficients. (Notice that this would not be correct if we replaced ≤ by <, since the right side of the equivalence would always be satisfied by b = 0.) Conversely, every set S represented by a formula of the above form is recursively enumerable. A basic unsolved problem is whether S can be defined using only existential quantifiers.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1956
References
1 See, for example, Kleene, S. C., Recursive predicates and quantifiers, Transactions of the American Mathematical Society, vol. 53 (1943), pp. 41–73CrossRefGoogle Scholar, Theorem I.
2 Davis, Martin, Arithmetical problems and recursively enumerable predicates, this Journal, vol. 18 (1953), pp. 33–41Google Scholar, Theorem 3.1.
3 Mostowski, Andrzej, On a set of integers not definable by means of one-quantifier predicates, Annales de la Société Polonaise de Mathématique, vol. 21 (1948), pp. 114–119Google Scholar, Theorem 3.3; Davis, loc. cit., Theorems 3.3 and 3.4.
4 Davis, loc. cit., Theorem 3.5.
5 Davis's results were stated for recursively enumerable sets in a space of any number of dimensions; using pairing functions, Theorem G can also be extended in this way.
6 In a somewhat similar (but simpler) problem, the author obtained a sharp result: The smallest number of quantifiers in an arithmetical definition of the set of natural numbers in the ring of integers is 2. See Robinson, R. M., Arithmetical definitions in the ring of integers, Proceedings of the American Mathematical Society, vol. 2 (1951), pp. 279–284CrossRefGoogle Scholar.
7 Robinson, R. M., Primitive recursive functions. II, Proceedings of the American Mathematical Society, vol. 6 (1955), pp. 663–666CrossRefGoogle Scholar, Theorem 2. This paper is a supplement to Primitive recursive functions, Bulletin of the American Mathematical Society, vol. 53 (1947), pp. 925–942CrossRefGoogle Scholar.
- 19
- Cited by


