An operator Γ mapping P(ω) to itself is inductive if Γ(A) ⊇ A for all A. For such an inductive operator Γ we define {Γα : α ∈ ORD} by letting Γ = ⌀, Γα + 1 = Γ(Γα ) for all α, and Γβ = ⋃{Γα : α < β} for limit ordinals β. The closure ordinal ∣Γ∣ of Γ is the least ordinal α such that Γα+1 = Γα and the closure 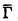is Γ∣Γ∣.

Let 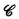be a class of operators over the natural numbers. The closure ordinal ∣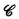∣ of 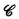is the supremum of {∣Γ∣: Γ is an inductive operator and 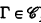}. The closure algebra 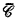generated by 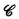is {A ⊆ ω: A is 1-1 reducible to 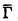for some inductive operator 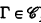}. The inductive algebra 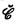generated by 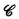is {Γα : Γ is an inductive operator in 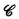and α < ∣Γ∣}.

For A ∈ P(ω), 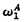is the supremum of the ordinals of well-orderings recursive in A. For 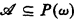, let 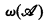be the supremum of 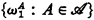. For example, it is well known that ω(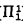) = ω(∆1 0 = ω 1, ω(Π1 1) = ω 1 and ω(Δn 1) = δn 1 for n > 1 (the latter by definition).