Let ε stand for the set of nonnegative integers (numbers), V for the class of all subcollections of ε(sets), Λ for the set of isols, ΛR for the set of regressive isols, and 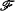for the set of mappings from a subset of ε into ε (functions). If ƒ is a function we write δƒ and ρƒ for its domain and range, respectively. We denote the inclusion relation by ⊃ and proper inclusion by ⊊. The sets α and β are recursively equivalent [written: α ≃ β], if δƒ = α and ρƒ = β for some function ƒ with a one-to-one partial recursive extension. We denote the recursive equivalence type of a set α, {σ ∈ V ∣ σ ≃ α} by Req(α). The reader is assumed to be familiar with the contents of [1], [2], [3], and [6].

The concept of an ω-group was introduced in [6], and that of an ω-homomorphism in [1]. However, except for a few examples, very little is known about the structure of ω-groups. If G is an ω-group and Π is an ω-homomorphism, then it follows that K = Ker Π and H = Π(G) are ω-groups. The question arises that if we know the structure of K and H, then what can we say about the structure of G? In this paper we will begin the study of ω-extensions, which will give us a partial answer to this question.