Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T22:18:48.671Z Has data issue: false hasContentIssue false
  • English
  • Français

An inelastic model with indiscernibles

Published online by Cambridge University Press:  12 March 2014

Julia F. Knight
Julia F. Knight*
Affiliation:
Pennsylvania State University, University Park, PA 16802
Get access Rights & Permissions [Opens in a new window]

Extract

Let L be a countable language including the unary relation symbol U. Let 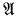and 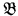be L-structures such that 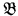is a proper elementary U-extension of 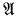; i.e., 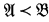, 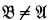and 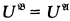. Under what conditions will 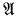have a proper elementary U-extension? In [2], it was shown that this is not always the case, even if 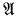and 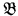are countable. However, the examples given are completely artificial, and it still seems that in most cases 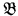will have a proper elementary U-extension.

Lascar asked whether 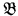will necessarily have a proper elementary U-extension whenever it contains an infinite set of indiscernibles over 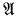. This paper gives a counterexample for Lascar's question. The example is produced by modifying one of the examples in [2], using an idea of Marcus [5].

Models containing an infinite set of indiscernibles can often be “stretched” to produce larger models that share some desired nonelementary property with the original [1], [6]. However, the mere presence of indiscernibles in a model does not guarantee that it can be used in this way.

If the model is not completely determined by the indiscernibles, the nonelementary property may not carry over to larger models. An example of this is given in [3]. The example for Lascar's question is further evidence that models with indiscernibles need not be “elastic”.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 2 , June 1978 , pp. 331 - 334
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Ehrenfeucht, A. and Mostowski, A., Models of axiomatic theories admitting automorphisms, Fundamenta Mathematicae, vol. 43 (1956), pp. 50–68.CrossRefGoogle Scholar
[2]Knight, J., Generic expansions of structures, this Journal, vol. 38 (1973), pp. 561–570.Google Scholar
[3]Knight, J., Omitting types in set theory and arithmetic, this Journal, vol. 41 (1976), pp. 25–32.Google Scholar
[4]Knight, J., Prime and atomic models, preprint.Google Scholar
[5]Marcus, L., A minimal model with an infinite set of indiscernibles, Israel Journal of Mathematics, vol. 11 (1972), pp. 180–183.CrossRefGoogle Scholar
[6]Morley, M., Categoricity in power, Transactions of the American Mathematical Society, vol. 114 (1965), pp. 514–538.CrossRefGoogle Scholar
[7]Shelah, S., Uniqueness and characterization of prime models over sets for totally transcendental first order theories, this Journal, vol. 37 (1972), pp. 107–113.Google Scholar
[8]Shelah, S., Categoricity in ℵ1, of sentences in Lω1ω(Q), Israel Journal of Mathematics, vol. 20 (1975), pp. 127–148.CrossRefGoogle Scholar