Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T04:27:19.009Z Has data issue: false hasContentIssue false
  • English
  • Français

An incorrect theorem1

Published online by Cambridge University Press:  12 March 2014

Theodore Hailperin
Theodore Hailperin*
Affiliation:
Sandia Laboratory, Albuquerque, New Mexico and, Lehigh University
Get access Rights & Permissions [Opens in a new window]

Extract

In the fourth edition of Hilbert-Ackermann's Grundzüge der Theoretischen Logik (Springer-Verlag: Berlin-Göttingen-Heidelberg 1959) the following assertion is “proved” (p. 131):

Ein Ausdruck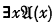, der keine freien Individuenvariablen enthält, ist dann und nur dann allgemeingültig, wenn 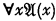allgemeingültig ist. Die Ausdrücke, die die Identität enthalten, sind dabei eingeschlossen.

As a counter example one can cite: ∃x(¬∃xFx ∨ Fx), which is universally valid yet the generalized form: ∀x(¬∃xFx ∨ Fx) is not (e.g. let the domain of individuals be the natural numbers and let ‘Fx’ be ‘x is factorable’).

It may be of interest to see where the alleged proof went astray. It is argued (correctly) that any expression 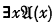can only be derived by the given rules from a formula 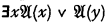, or from this formula with any other variable in place of y. Moreover (still correctly) any upper formula of such a formula is of the form 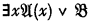(“Upper formula” in the transitive sense of an upper formula of an upper formula being an upper formula). But then it is stated (incorrectly) that if 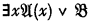is an upper formula of 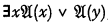, then 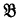is an upper formula of 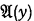. To show that this is incorrect we here append a proof of the universally valid formula mentioned above:

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 30 , Issue 1 , March 1965 , pp. 27
Copyright
Copyright © Association for Symbolic Logic 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

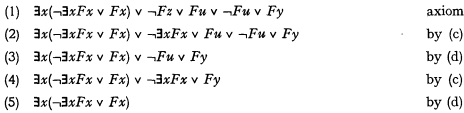
This work was supported by the United States Atomic Energy Commission. Reproduction in whole or in part is permitted for any purpose of the U.S. Government.

References

1 This work was supported by the United States Atomic Energy Commission. Reproduction in whole or in part is permitted for any purpose of the U.S. Government.