Hostname: page-component-55f67697df-twqc4 Total loading time: 0 Render date: 2025-05-09T18:24:48.570Z Has data issue: false hasContentIssue false
  • English
  • Français

AN INCOMPLETENESS THEOREM VIA ORDINAL ANALYSIS

Part of: Proof theory and constructive mathematics

Published online by Cambridge University Press:  12 September 2022

JAMES WALSH
JAMES WALSH*
Affiliation:
SAGE SCHOOL OF PHILOSOPHY CORNELL UNIVERSITY ITHACA, NY 14850, USA
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an analogue of Gödel’s second incompleteness theorem for systems of second-order arithmetic. Whereas Gödel showed that sufficiently strong theories that are 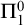$\Pi ^0_1$-sound and 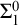$\Sigma ^0_1$-definable do not prove their own 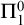$\Pi ^0_1$-soundness, we prove that sufficiently strong theories that are 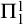$\Pi ^1_1$-sound and 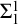$\Sigma ^1_1$-definable do not prove their own 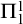$\Pi ^1_1$-soundness. Our proof does not involve the construction of a self-referential sentence but rather relies on ordinal analysis.

Keywords

proof theorysecond-order arithmeticordinal analysisincompleteness

MSC classification

Primary: 03F15: Recursive ordinals and ordinal notations 03F40: Gödel numberings and issues of incompleteness
Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 1 , March 2024 , pp. 80 - 96
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aguilera, J. P. and Pakhomov, F., The ${\varPi}_2^1$ consequences of a theory, preprint, 2021, arXiv:2109.11652.CrossRefGoogle Scholar
Beckmann, A. and Pohlers, W., Applications of cut-free infinitary derivations to generalized recursion theory . Annals of Pure and Applied Logic , vol. 94 (1998), nos. 1–3, pp. 7–19.CrossRefGoogle Scholar
Beklemishev, L. D., Induction rules, reflection principles, and provably recursive functions . Annals of Pure and Applied Logic , vol. 85 (1997), no. 3, pp. 193–242.CrossRefGoogle Scholar
Buchholz, W., Notation systems for infinitary derivations . Archive for Mathematical Logic , vol. 30 (1991), nos. 5–6, pp. 277–296.CrossRefGoogle Scholar
Gentzen, G., Provability and nonprovability of restricted transfinite induction in elementary number theory , The Collected Papers of Gerhard Gentzen (M. E. Szabo, editor), North-Holland, Amsterdam, 1969, pp. 287–308.CrossRefGoogle Scholar
Kotlarski, H., The incompleteness theorems after 70 years . Annals of Pure and Applied Logic , vol. 126 (2004), nos. 1–3, pp. 125–138.CrossRefGoogle Scholar
Lutz, P. and Walsh, J., Incompleteness and jump hierarchies . Proceedings of the American Mathematical Society , vol. 148 (2020), no. 11, pp. 4997–5006.CrossRefGoogle Scholar
Pakhomov, F. and Walsh, J., Reflection ranks and ordinal analysis, this Journal, vol. 86 (2021), pp. 1350–1384.Google Scholar
Pakhomov, F. and Walsh, J., Reflection ranks via infinitary derivations, preprint, 2021, arXiv:2107.03521.Google Scholar
Pohlers, W., Proof Theory: An Introduction , Lecture Notes in Mathematics, vol. 1407 Springer, Berlin–Heidelberg, 1989, p. VI-213.Google Scholar
Pohlers, W., Subsystems of set theory and second order number theory . Handbook of Proof Theory , (Buss, S., editor) vol. 137 (1998), pp. 209–335.CrossRefGoogle Scholar
Rathjen, M., The role of parameters in bar rule and bar induction, this Journal, vol. 56 (1991), no. 2, pp. 715–730.Google Scholar
Rathjen, M., The realm of ordinal analysis, Sets and Proofs (S. Barry Cooper and J. K. Truss, editors), London Mathematical Society Lecture Note Series, Cambridge University Press, New York, 1999, pp. 219–280.CrossRefGoogle Scholar
Sacks, G. E., Higher Recursion Theory, vol. 2 , Cambridge University Press, Cambridge University Press, New York, 2017.CrossRefGoogle Scholar
Salehi, S.. On the diagonal lemma of Gödel and Carnap . Bulletin of Symbolic Logic , vol. 26 (2020), no. 1, pp. 80–88.CrossRefGoogle Scholar
Visser, A., From Tarski to Gödel—Or how to derive the second incompleteness theorem from the undefinability of truth without self-reference . Journal of Logic and Computation , vol. 29 (2019), no. 5, pp. 595–604.CrossRefGoogle Scholar
Walsh, J., On the hierarchy of natural theories, preprint, 2021, arXiv:2106.05794.Google Scholar