Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-19T09:46:43.559Z Has data issue: false hasContentIssue false
  • English
  • Français

An incompleteness theorem for βn-models

Published online by Cambridge University Press:  12 March 2014

Carl Mummert  and
Stephen G. Simpson
Carl Mummert
Affiliation:
Department of Mathematics, Pennsylvania State University, State College, PA 16802, USA, URL: http://www.math.psu.edu/mummert/, E-mail: [email protected]
Stephen G. Simpson
Affiliation:
Department of Mathematics, Pennsylvania State University, State College, PA 16802, USA, URL: http://www.math.psu.edu/simpson/, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

Let n be a positive integer. By a βn-model we mean an ω-model which is elementary with respect to 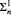formulas. We prove the following βn-model version of Gödel's Second Incompleteness Theorem. For any recursively axiomatized theory S in the language of second order arithmetic, if there exists a βn-model of S, then there exists a βn-model of S + “there is no countable βn-model of S”. We also prove a βn-model version of Löb's Theorem. As a corollary, we obtain a βn-model which is not a βn+1-model.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 2 , June 2004 , pp. 612 - 616
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Blass, Andreas R., Hirst, Jeffry L., and Simpson, Stephen G., Logical analysis of some theorems of combinatorics and topological dynamics, in [9], 1987, pp. 125–156.CrossRefGoogle Scholar
[2]Enderton, Herbert B. and Friedman, Harvey, Approximating the standard model of analysis, Fundamenta Mathematicae, vol. 72 (1971), no. 2, pp. 175–188.CrossRefGoogle Scholar
[3]Engström, Fredrik, October 2003, Private communication.Google Scholar
[4]Friedman, Harvey, Subsystems of Set Theory and Analysis, Ph.D. thesis, Massachusetts Institute of Technology, 1967.Google Scholar
[5]Friedman, Harvey, Uniformly defined descending sequences of degrees, this Journal, vol. 41 (1976), pp. 363–367.Google Scholar
[6]Gödel, Kurt, Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I, Monatshefte für Mathematik und Physik, vol. 38 (1931), pp. 173–198.CrossRefGoogle Scholar
[7]Löb, M. H., Solution of a problem of Leon Henkln, this Journal, vol. 20 (1955), pp. 115–118.Google Scholar
[8]Shilleto, J. R., Minimum models of analysis, this Journal, vol. 37 (1972), pp. 48–54.Google Scholar
[9]Simpson, S. G. (editor), Logic and Combinatorics, Contemporary Mathematics, American Mathematical Society, 1987.CrossRefGoogle Scholar
[10]Simpson, Stephen G., Subsystems of Second Order Arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, 1999.CrossRefGoogle Scholar
[11]Steel, John R., Descending sequences of degrees, this Journal, vol. 40 (1975). pp. 59–61.Google Scholar