Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-22T20:20:04.523Z Has data issue: false hasContentIssue false
  • English
  • Français

An improved prenex normal form1

Published online by Cambridge University Press:  12 March 2014

C. C. Chang  and
H. Jerome Keisler
C. C. Chang
Affiliation:
University of California, Los Angeles University of California, Berkeley California Institute of Technology, Pasadena
H. Jerome Keisler
Affiliation:
University of California, Los Angeles University of California, Berkeley California Institute of Technology, Pasadena
Get access Rights & Permissions [Opens in a new window]

Extract

Let ℒ be the set of all formulas of a given first order predicate logic (with or without identity). For each positive integer n, let ℒn be the set of all formulas φ in ℒ logically equivalent to a formula of the form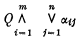

where Q is a (possibly empty) string of quantifiers, m is a positive integer, and each αij is either an atomic formula or the negation of an atomic formula.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 27 , Issue 3 , September 1962 , pp. 317 - 326
Copyright
Copyright © Association for Symbolic Logic 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The work of the first named author was supported by a research grant from the National Science Foundation. The work of the second named author was supported by a National Science Foundation Cooperative Fellowship.

References

2 Before arriving at the final result, the bound on the length of the disjunctions in the improved normal form took, with the passage of time, the following values (in the opinion of the authors): 3·p + 2p, 4·p, 3·p + 2p, 5·p, 3·p, max(3, p), and finally, in the case of logic with identity, max (2, p). The authors became interested in this problem through their investigations on reduced products in the theory of models. Chronologically, the results of § 2 preceded those of § 1. In the light of the methods of § 1, the proofs in § 2 were considerably simplified.