Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-13T07:06:14.956Z Has data issue: false hasContentIssue false
  • English
  • Français

An extension of the nondiamond theorem in classical and α-recursion theory

Published online by Cambridge University Press:  12 March 2014

Klaus Ambos-Spies
Klaus Ambos-Spies*
Affiliation:
Universität Dortmund, Dortmund, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Lachlan's nondiamond theorem [7, Theorem 5] asserts that there is no embedding of the four-element Boolean algebra (diamond) in the recursively enumerable degrees which preserves infima, suprema, and least and greatest elements. Lachlan observed that, essentially by relativization, the theorem can be extended to

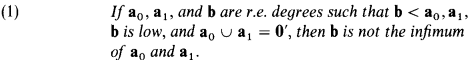
Using the Sacks splitting theorem he concluded that there exists a pair of r.e. degrees which does not have an infimum, thus showing that the r.e. degrees do not form a lattice.

We will first prove the following extension of (1):

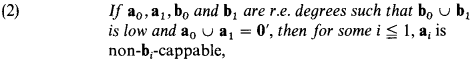
where an r.e. degree a is non-b-cappable if 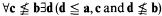. From (2) we obtain more information about pairs of r.e. degrees without infima: For every nonzero low r.e. degree there exists an incomparable one such that the two degrees do not have an infimum and there is an r.e. degree which is not half of a pair of incomparable r.e. degrees which has an infimum in the low r.e. degrees. Probably the most interesting corollary of (2) is that the join of any cappable r.e. degree (i.e. half of a minimal pair) and any low r.e. degree is incomplete. Consequently there is an incomplete noncappable degree above every incomplete r.e. degree. Cooper's result [3] that ascending sequences of uniformly r.e. degrees can have minimal upper bounds in the set R of r.e. degrees is another corollary of (2).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 2 , June 1984 , pp. 586 - 607
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ambos-Spies, K., On the structure of the recursively enumerable degrees, Dissertation, Universität München, Munich, 1980.Google Scholar
[2]Ambos-Spies, K., On pairs of recursively enumerable degrees, Transactions of the American Mathematical Society (to appear).Google Scholar
[3]Cooper, S. B., Minimal upper bounds for sequences of recursively enumerable degrees, Journal of the London Mathematical Society, vol. 5 (1972), pp. 445–450.CrossRefGoogle Scholar
[4]Fejer, P. A., Structure of r.e. degrees (Abstract), Conference on Mathematical Logic, Storrs, Connecticut, 1979.Google Scholar
[5]Fejer, P. A., and Soare, R. I., The plus-cupping theorem for the recursively enumerable degrees, Logic Year 1979-80, Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 49–62.CrossRefGoogle Scholar
[6]Friedberg, R. M., Two recursively enumerable sets of incomparable degrees of unsolvability, Proceedings of the National Academy of Sciences of the U.S.A., vol. 43 (1957), pp. 236–238.CrossRefGoogle ScholarPubMed
[7]Lachlan, A. H., Lower bounds for pairs of r.e. degrees, Proceedings of the London Mathematical Society, ser. 3, vol. 16 (1966), pp. 537–569.CrossRefGoogle Scholar
[8]Lachlan, A. H., Decomposition of recursively enumerable degrees, Proceedings of the American Mathematical Society, vol. 79 (1980), pp. 629–634.CrossRefGoogle Scholar
[9]Lerman, M., On suborderings of the α.-recursively enumerable α-degrees, Annals of Mathematical Logic, vol. 4 (1972), pp. 369–392.CrossRefGoogle Scholar
[10]Lerman, M., Least upper bounds for minimal pairs of a-r.e. x-degrees, this Journal, vol. 39 (1974), pp. 49–56.Google Scholar
[11]Lerman, M. and Sacks, G. E., Some minimal pairs of x-recursively enumerable degrees, Annals of Mathematical Logic, vol. 4 (1972), pp. 415–442.CrossRefGoogle Scholar
[12]Miller, D. P., High recursively enumerable degrees and the anti-cupping property, Logic Year 1979-80, Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 230–245.CrossRefGoogle Scholar
[13]Muchnik, A. A., Negative answer to the problem of reducibility of the theory of algorithms (Russian), Doklady Akadémii Nauk SSSR, vol. 108 (1956), pp. 194–197.Google Scholar
[14]Robinson, R. W., Interpolation and embedding in the recursively enumerable degrees, Annals of Mathematics, vol. 93 (1971), pp. 285–314.CrossRefGoogle Scholar
[15]Sacks, G. E., Degrees of unsolvability, Annals of Mathematics Studies, vol. 55, Princeton University Press, Princeton, N.J., 1963.Google Scholar
[16]Shore, R. A., Splitting an α-recursively enumerable set, Transactions of the American Mathematical Society, vol. 204 (1975), pp. 65–77.Google Scholar
[17]Shore, R. A., On the jump of an α-recursively enumerable set, Transactions of the American Mathematical Society, vol. 217 (1976), pp. 351–363.Google Scholar
[18]Shore, R. A., >On the π∃-sentences of α-recursion theory, Generalized recursion theory. II (Fenstad, J. E., Gandy, R. O. and Sacks, G. E., editors), North-Holland, Amsterdam, 1978, pp. 331–353.Google Scholar
[19]Shore, R. A., Some constructions in α-recursion theory, Recursion theory: its generalisations and applications, London Mathematical Society Lecture Notes Series, vol. 45, Cambridge University Press, Cambridge, 1980, pp. 158–170.CrossRefGoogle Scholar
[20]Simpson, S. G., Degree theory on admissible ordinals, Generalized recursion theory (Fenstad, J. E. and Hinman, P. G., editors), North-Holland, Amsterdam, 1974, pp. 165–193.Google Scholar
[21]Soare, R. I., The Friedberg-Muchnik theorem re-examined, Canadian Journal of Mathematics, vol. 24 (1972), pp. 1070–1078.CrossRefGoogle Scholar
[22]Soare, R. I., Computational complexity, speedable and levelable sets, this Journal, vol. 42 (1977), pp. 545–563.Google Scholar
[23]Soare, R. I., Fundamental methods for constructing recursively enumerable degrees, Recursion theory: its generalisations and applications, London Mathematical Society Lecture Notes Series, vol. 45, Cambridge University Press, Cambridge, 1980, pp. 1–51.Google Scholar
[24]Yates, C. E. M., A minimal pair of r.e. degrees, this Journal, vol. 31 (1966), pp. 159–168.Google Scholar
[25]Yates, C. E. M., On the degrees of index sets. II, Transactions of the American Mathematical Society, vol. 135 (1969), pp. 249–266.CrossRefGoogle Scholar