Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Howard, Mark
1989.
Applications of Fodor's lemma to Vaught's conjecture.
Annals of Pure and Applied Logic,
Vol. 42,
Issue. 1,
p.
1.
Solecki, Sławomir
1995.
Equivalence relations induced by actions of Polish groups.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 12,
p.
4765.
Camerlo, Riccardo
and
Kechris, Alexander S.
2000.
Countable structures with a fixed group of automorphisms.
Israel Journal of Mathematics,
Vol. 117,
Issue. 1,
p.
105.
2000.
Computable Structures and the Hyperarithmetical Hierarchy.
Vol. 144,
Issue. ,
p.
323.
HJORTH, GREG
2002.
KNIGHT'S MODEL, ITS AUTOMORPHISM GROUP, AND CHARACTERIZING THE UNCOUNTABLE CARDINALS.
Journal of Mathematical Logic,
Vol. 02,
Issue. 01,
p.
113.
Keisler, H. Jerome
and
Knight, Julia F.
2004.
Barwise: Infinitary Logic and Admissible Sets.
Bulletin of Symbolic Logic,
Vol. 10,
Issue. 1,
p.
4.
Calvert, Wesley
and
Knight, Julia F.
2006.
Classification from a Computable Viewpoint.
Bulletin of Symbolic Logic,
Vol. 12,
Issue. 2,
p.
191.
Goncharov, Sergei S.
2007.
Mathematical Problems from Applied Logic II.
Vol. 5,
Issue. ,
p.
99.
Sacks, Gerald E.
2007.
Bounds on Weak Scattering.
Notre Dame Journal of Formal Logic,
Vol. 48,
Issue. 1,
Gao, Su
2007.
Complexity Ranks of Countable Models.
Notre Dame Journal of Formal Logic,
Vol. 48,
Issue. 1,
Millar, J.
and
Sacks, G.E.
2008.
Atomic models higher up.
Annals of Pure and Applied Logic,
Vol. 155,
Issue. 3,
p.
225.
Calvert, W.
Goncharov, S. S.
Knight, J. F.
and
Millar, Jessica
2009.
Categoricity of computable infinitary theories.
Archive for Mathematical Logic,
Vol. 48,
Issue. 1,
p.
25.
KNIGHT, J. F.
and
MILLAR, J.
2010.
COMPUTABLE STRUCTURES OF RANK $\omega_{1}^{{\rm CK}}$.
Journal of Mathematical Logic,
Vol. 10,
Issue. 01n02,
p.
31.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Chan, William
2017.
The countable admissible ordinal equivalence relation.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 6,
p.
1224.
Becker, Howard
2017.
Strange Structures from Computable Model Theory.
Notre Dame Journal of Formal Logic,
Vol. 58,
Issue. 1,
Harrison-Trainor, Matthew
2018.
Scott ranks of models of a theory.
Advances in Mathematics,
Vol. 330,
Issue. ,
p.
109.
Harrison-Trainor, Matthew
Igusa, Gregory
and
Knight, Julia
2018.
Some new computable structures of high rank.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 7,
p.
3097.
HARRISON-TRAINOR, MATTHEW
2022.
AN INTRODUCTION TO THE SCOTT COMPLEXITY OF COUNTABLE STRUCTURES AND A SURVEY OF RECENT RESULTS.
The Bulletin of Symbolic Logic,
Vol. 28,
Issue. 1,
p.
71.
MONTALBÁN, ANTONIO
and
ROSSEGGER, DINO
2024.
THE STRUCTURAL COMPLEXITY OF MODELS OF ARITHMETIC.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 4,
p.
1703.
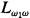 .
.

