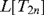Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T20:23:12.308Z Has data issue: false hasContentIssue false
  • English
  • Français

AN ANALYSIS OF THE MODELS $L[T_{2n} ]$

Published online by Cambridge University Press:  04 February 2019

RACHID ATMAI
RACHID ATMAI*
Affiliation:
DEPARTMENT OF MATHEMATICS MIRACOSTA COLLEGE OCEANSIDE, CA 92056, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyze the models 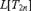$L[T_{2n} ]$, where 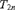$T_{2n}$ is a tree on 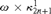$\omega \times \kappa _{2n + 1}^1 $ projecting to a universal 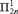${\rm{\Pi }}_{2n}^1 $ set of reals, for 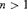$n > 1$. Following Hjorth’s work on 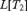$L[T_2 ]$, we show that under 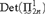${\rm{Det}}\left( {{\rm{}}_{2n}^1 } \right)$, the models 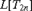$L[T_{2n} ]$ are unique, that is they do not depend of the choice of the tree 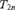$T_{2n}$. This requires a generalization of the Kechris–Martin theorem to all pointclasses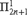${\rm{\Pi }}_{2n + 1}^1$. We then characterize these models as constructible models relative to the direct limit of all countable nondropping iterates of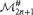${\cal M}_{2n + 1}^\# $. We then show that the GCH holds in 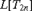$L[T_{2n} ]$, for every $n < \omega $, even though they are not extender models. This analysis localizes the HOD analysis of Steel and Woodin at the even levels of the projective hierarchy.

Keywords

03E1503E45descriptive set theoryinner model theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 1 - 26
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Atmai, R., Contributions to descriptive set theory, Ph.D. thesis, University of North Texas, 2015.Google Scholar
Becker, H. S. and Kechris, A. S., Sets of ordinals constructible from trees and the third Victoria Delfino problem, Axiomatic Set Theory (Boulder, Colorado, 1983 ) (Baumgartner, J. E., Martin, D. A., and Shelah, S., editors), Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, RI, 1984, pp. 13–29.Google Scholar
Hjorth, G., Variations of the Martin-Solovay tree, this Journal, vol. 61 (1996), no. 1, pp. 40–51.Google Scholar
Jackson, S., Structural consequences of AD, Handbook of Set Theory, vol. 3 (Foreman, M. and Kanamormi, A., editors), Springer, Dordrecht, 2010, pp. 1753–1876.10.1007/978-1-4020-5764-9_22CrossRefGoogle Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Kechris, A. S., Countable ordinals and the analytical hierarchy. II. Annals of Mathematical Logic, vol. 15 (1978), no. 3, pp. 193–223 (1979).10.1016/0003-4843(78)90010-4CrossRefGoogle Scholar
Kechris, A. S., Forcing in analysis, Higher Set Theory, Lecture Notes in Mathematics, vol. 669, Springer, Berlin, 1978, pp. 277–302.10.1007/BFb0103105CrossRefGoogle Scholar
Kechris, A. S., AD and projective ordinals, Cabal Seminar 76–77 (Kechris, A. S. and Moschovakis, Y. N., editors), Lecture Notes in Mathematics, vol. 689, Springer, Berlin, 1978, pp. 91–132.10.1007/BFb0069296CrossRefGoogle Scholar
Kechris, A. S. and Donald, M. A., On the theory of ${\rm{\Pi }}_3^1 $ sets of reals, II, Ordinal Definability and Recursion Theory. The Cabal Seminar, vol. III (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic, vol. 43, Association for Symbolic Logic, La Jolla, CA, Cambridge University Press, Cambridge, 2016.10.1017/CBO9781139519694CrossRefGoogle Scholar
Kechris, A. S., Martin, D. A., and Solovay, R. M., Introduction to Q-theory, Cabal Seminar 79–81 (Kechris, A. S., Martin, D. A., and Moschovakis, Y. N., editors), Lecture Notes in Mathematics, vol. 1019, Springer, Berlin, 1983, pp. 199–282.10.1007/BFb0071702CrossRefGoogle Scholar
Kechris, A. S. and Solovay, R. M., On the relative consistency strength of determinacy hypotheses. Transactions of the American Mathematical Society, vol. 290 (1985), no. 1, pp. 179–211.Google Scholar
Koellner, P. and Woodin, W. H., Large cardinals from determinacy, Handbook of Set Theory, vol. 3 (Foreman, M. and Kanamormi, A., editors), Springer, Dordrecht, 2010, pp. 1951–2119.10.1007/978-1-4020-5764-9_24CrossRefGoogle Scholar
Moschovakis, Y. N., Descriptive Set Theory, Studies in Logic and the Foundations of Mathematics, vol. 100, North-Holland, Amsterdam, 1980.Google Scholar
Steel, J. R., Projectively well-ordered inner models. Annals of Pure and Applied Logic, vol. 74 (1995), no. 1, pp. 77–104.10.1016/0168-0072(94)00021-TCrossRefGoogle Scholar
Steel, J. R., Scales in $K\left( \right)$ at the end of a weak gap , this Journal, vol. 73 (2008), no. 2, pp. 369–390.Google Scholar
Steel, J. R., ${\rm{HOD}}^{L\left( \right)}$ is a core model below ${\rm{\Theta }}$. Bulletin of Symbolic Logic, vol. 1 (1995), no. 1, pp. 75–84.10.2307/420947CrossRefGoogle Scholar
Steel, J. R., An outline of inner model theory, Handbook of Set Theory, vol. 3 (Foreman, M. and Kanamormi, A., editors), Springer, Dordrecht, 2010, pp. 1595–1684.10.1007/978-1-4020-5764-9_20CrossRefGoogle Scholar
Steel, J. R. and Hugh, W. W., HOD as a core model, Ordinal Definability and Recursion Theory. The Cabal Seminar, vol. III (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic, vol. 43, Association for Symbolic Logic, La Jolla, CA, Cambridge University Press, Cambridge, 2016, pp. 257–346.10.1017/CBO9781139519694.010CrossRefGoogle Scholar