Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T02:16:48.507Z Has data issue: false hasContentIssue false
  • English
  • Français

An absoluteness principle for Borel sets

Published online by Cambridge University Press:  12 March 2014

Greg Hjorth
Greg Hjorth*
Affiliation:
Mathematics Department, University of California, Los Angeles, Los Angeles, California 90095-1555, USA, E-mail: [email protected], URL: www.math.ucla.edu/~greg
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of these notes is to describe an absoluteness principle due to Jacques Stern and discuss some applications to the general study of Borel sets. This paper will not be engaged in independence results, but in proving outright theorems about the Borel hierarchy.

Roughly speaking, Stern's absoluteness principle states that if a certain 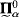set can be introduced into the universe by forcing, then it can be introduced by some small forcing notion.

The notation 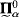, and so on, will be defined in Section 1; this gives a notational system for describing the complexity of Borel sets beyond Fσ or Gδ. The “universe” refers to the totality of all sets. “Forcing” refers to Paul Cohen's technique for, in some sense, changing this totality by the introduction of new sets. Here “small” means relatively small cardinality.

The size of this small forcing notion is roughly the ath iteration of the power set operation. Just to get an idea of what this theorem might be saying, we can argue that under certain conditions, if a closed set can be introduced by forcing, then it exists already. There are a number of other qualifications that need to be made to this rough description, and we will come to them later.

Unlike, say, Shoenfield absoluteness, Stern's absoluteness can only be made understood in the terminology of forcing. Since forcing is typically associated with the pursuit of independence results, we could easily assume that Stern's work has little relevance in proving positive theorems about the Borel hierarchy.

However, this would be untrue. Using abstract and indirect metamathematical arguments, and availing ourselves of Stern's absoluteness principle, we will prove a string of ZFC theorems for which no direct proof is known.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 2 , June 1998 , pp. 663 - 693
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Becker, H. and Kechris, A. S., The descriptive set theory of Polish group actions, London Mathematical Society Lecture Notes Series, Cambridge, 1996.10.1017/CBO9780511735264Google Scholar
[2] Burgess, J., Effective enumeration of classes in a equivalence relation, Indiana University Mathematics Journal, vol. 20 (1979), pp. 353–364.Google Scholar
[3] Fremlin, D. H. and Shelah, S., Decomposing the real line into ℵ1 many G δσ sets, Israel Journal of Mathematics, vol. 32 (1979), pp. 299–304.Google Scholar
[4] Friedman, H., On the necessary use ofabstract set theory, Advances in Mathematics, vol. 41 (1981), pp. 209–280.10.1016/0001-8708(81)90021-9Google Scholar
[5] Harrington, L., Analytic determinacy and 0# , this Journal, vol. 43 (1978), pp. 685–693.Google Scholar
[6] Hjorth, G. and Kechris, A., Analytic equivalence relations and Ulm-type classifications, this Journal, vol. 60 (1995), pp. 1273–1300.Google Scholar
[7] Kanovei, V., Undecidable and decidable properties of constituents, Mathematics of USSR Sbornik, vol. 124 (1984), pp. 491–519.Google Scholar
[8] Kechris, A. S., Polish group actions and definable equivalence relations, unpublished manuscript, 1994.Google Scholar
[9] Kechris, A. S. and Louveau, A., The structure of hypersmooth Borel equivalence relations, Journal of the American Mathematical Society, vol. 10 (1997), pp. 215–242.Google Scholar
[10] Louveau, A., A separation theorem for sets, Transactions of the American Mathematical Society, vol. 260 (1980), pp. 363–378.Google Scholar
[11] Makkai, M., An example concerning Scott heights, this Journal, vol. 46 (1981), pp. 301–315.Google Scholar
[12] Martin, D. A., Determinacy, unpublished manuscript.Google Scholar
[13] Martin, D. A. and Solovay, R., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), pp. 143–178.10.1016/0003-4843(70)90009-4Google Scholar
[14] Martin, D. A. and Steel, J., The extent of scales in L(ℝ), Cabal seminar 79–81, Lecture Notes in Mathematics, Springer-Verlag, pp. 86–96.Google Scholar
[15] Moschovakis, Y. N., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[16] Sami, R., On equivalence relations with Borel classes of bounded rank, this Journal, vol. 49 (1984), pp. 1273–1283.Google Scholar
[17] Sami, R., Polish group actions and the topological Vaught conjecture, Transactions of the American Mathematical Society, vol. 341 (1994), pp. 335–353.10.1090/S0002-9947-1994-1022169-2Google Scholar
[18] Silver, J., Counting the number of equivalence classes of Borel or co-analytic equivalence relations, Annals of Mathematical Logic, vol. 18 (1980), pp. 1–28.Google Scholar
[19] Solecki, S., Equivalence relations induced by actions of Polish groups, Transactions of the American Mathematical Society, vol. 347 (1995), pp. 4765–4777.10.1090/S0002-9947-1995-1311918-2Google Scholar
[20] Solovay, R., A model of set theory in which every set of reals is Lebesgue measurable, Annals of Mathematics, vol. 92 (1970), pp. 1–56.Google Scholar
[21] Stern, J., On Lusin's restricted continuum problem, Annals of Mathematics, vol. 120 (1984), pp. 7–37.Google Scholar