Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-31T19:00:44.679Z Has data issue: false hasContentIssue false
  • English
  • Français

AMALGAMABLE DIAGRAM SHAPES

Published online by Cambridge University Press:  05 February 2019

RUIYUAN CHEN
RUIYUAN CHEN*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF ILLINOIS AT URBANA–CHAMPAIGN URBANA, IL 61801, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A category has the amalgamation property (AP) if every pushout diagram has a cocone, and the joint embedding property (JEP) if every finite coproduct diagram has a cocone. We show that for a finitely generated category I, the following are equivalent: (i) every I-shaped diagram in a category with the AP and the JEP has a cocone; (ii) every I-shaped diagram in the category of sets and injections has a cocone; (iii) a certain canonically defined category 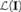${\cal L}\left( {\bf{I}} \right)$ of “paths” in I has only idempotent endomorphisms. When I is a finite poset, these are further equivalent to: (iv) every upward-closed subset of I is simply-connected; (v) I can be built inductively via some simple rules. Our proof also shows that these conditions are decidable for finite I.

Keywords

Primary 18A30Secondary 03C30amalgamation propertyFraïssé limitspushoutsinverse categories
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 88 - 101
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barmak, J. A., Algebraic Topology of Finite Topological Spaces and Applications, Lecture Notes in Mathematics, vol. 2032, Springer, Heidelberg, 2011.Google Scholar
Caramello, O., Fraïssé’s construction from a topos-theoretic perspective, Logica Universalis, vol. 8 (2014), no. 2, pp. 261–281.CrossRefGoogle Scholar
Cockett, J. R. B. and Lack, S., Restriction categories I: Categories of partial maps, Theoretical Computer Science, vol. 270 (2002), pp. 223–259.CrossRefGoogle Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Kubiś, W., Fraïssé sequences: Category-theoretic approach to universal homogeneous structures, Annals of Pure and Applied Logic, vol. 165 (2014), no. 11, pp. 1755–1811.CrossRefGoogle Scholar
Lawson, M. V., Inverse Semigroups: The Theory of Partial Symmetries, World Scientific Publishing Company, Singapore, 1998.CrossRefGoogle Scholar
Linckelmann, M., On inverse categories and transfer in cohomology, Proceedings of the Edinburgh Mathematical Society, vol. 56 (2013), no. 1, pp. 187–210.CrossRefGoogle Scholar
Lyndon, R. C. and Schupp, P. E., Combinatorial Group Theory, Springer-Verlag, Berlin, 1977.Google Scholar
Mac Lane, S., Categories for the Working Mathematician, second ed., Graduate Texts in Mathematics, vol. 5, Springer, New York, 1998.Google Scholar
Miller, C. F., Decision problems for groups – Survey and reflections, Algorithms and Classification in Combinatorial Group Theory (Baumslag, G. and Miller, C. F., editors), Mathematical Sciences Research Institute Publications, vol. 23, Springer, New York, 1992, pp. 1–59.CrossRefGoogle Scholar
Paré, R., Simply connected limits, Canadian Journal of Mathematics, vol. XLII (1990), no. 4, pp. 731–746.CrossRefGoogle Scholar
Quillen, D., Higher algebraic K-theory: I, Algebraic K-Theory (Bass, H., editor), Lecture Notes in Mathematics, vol. 341, Springer, Berlin, 1972, pp. 85–147.Google Scholar