Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T14:44:35.707Z Has data issue: false hasContentIssue false
  • English
  • Français

ALMOST GALOIS ω-STABLE CLASSES

Published online by Cambridge University Press:  22 July 2015

JOHN T. BALDWIN ,
PAUL B. LARSON  and
SAHARON SHELAH
JOHN T. BALDWIN
Affiliation:
DEPARTMENT OF MATHEMATICS STATISTICS AND COMPUTER SCIENCE UNIVERSITY OF ILLINOIS AT CHICAGO USAE-mail: [email protected]
PAUL B. LARSON
Affiliation:
DEPARTMENT OF MATHEMATICS MIAMI UNIVERSITY OXFORD, OHIO, USAE-mail: [email protected]
SAHARON SHELAH
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERSUSALEM JERUSALEM 91904 ISRAEL and DEPARTMENT OF MATHEMATICS RUTGERS, THE STATE UNIVERSITY OF NEW JERSEY PISCATAWAY, NEW JERSEY 08854-8019, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Theorem. Suppose that k = (K, 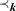$$\prec_k$$) is an ℵ0-presentable abstract elementary class with Löwenheim–Skolem number ℵ0, satisfying the joint embedding and amalgamation properties in ℵ0. If K has only countably many models in ℵ1, then all are small. If, in addition, k is almost Galois ω-stable then k is Galois ω-stable. Suppose that k = (K, $$\prec_k$$) is an ℵ0-presented almost Galois ω-stable AEC satisfying amalgamation for countable models, and having a model of cardinality ℵ1. The assertion that K is ℵ1-categorical is then absolute.

Keywords

03C4803C4503C75abstract elementary classalmost Galois stableabsoluteness
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 3 , September 2015 , pp. 763 - 784
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baldwin, John T., Categoricity, University Lecture Notes, vol. 51, American Mathematical Society, Providence, RI, 2009, www.math.uic.edu/∼jbaldwin.Google Scholar
Baldwin, John T., Amalgamation, absoluteness, and categoricity, Proceedings of the 11th Asian Logic Conference, 2009 (Arai, , Feng, , Kim, , Wu, , and Yang, , editors), pp. 22–50, World Scientific Publisher, Hackensack, NJ, 2012.Google Scholar
Baldwin, J. T., Friedman, Sy, Koerwien, M., and Laskowski, C., Three red herrings around vaught’s conjecture, Transactions of the American Mathematical Society, to appear.Google Scholar
Baldwin, J. T., Hyttinen, T., and Kesälä, M., Beyond first order logic: From number of structures to structure of numbers part II. Bulletin of Iranian Mathematical Society, vol. 39 (2013), no. 1, pp. 27–48, available online at http://www.iranjournals.ir/ims/bulletin/.Google Scholar
Baldwin, J. T. and Larson, Paul, Iterated elementary embeddings and the model theory of infinitary logic, preprint, http://homepages.math.uic.edu/∼jbaldwin/pub/.Google Scholar
Boney, W., Computing the number of types of infinite length, preprint.Google Scholar
Enayat, A., On certain elementary extensions of models of set theory. Transactions of the American Mathematical Society, vol. 283 (1984), pp. 705–715.CrossRefGoogle Scholar
Gao, Su, Invariant Descriptive Set Theory, CRC Press, Boca Raton, FL, 2009.Google Scholar
Harnik, V. and Makkai, M., A tree argument in infinitary model theory. Proceeedings of the American Mathematical Society, vol. 67 (1977), pp. 309–314.CrossRefGoogle Scholar
Hutchinson, John E., Elementary extensions of countable models of set theory, this Journal, vol. 41 (1976), pp. 139–145.Google Scholar
Hyttinen, T. and Kesälä, M., Independence in finitary abstract elementary classes. Annals of Pure and Applied Logic, vol. 143 (2006), no. 1–3, pp. 103–138.CrossRefGoogle Scholar
Jarden, A. and Shelah, S., Non-forking frames in abstract elementary classes. Annals Pure and Applied Logic, vol. 164 (2013), pp. 135–191.CrossRefGoogle Scholar
Keisler, H. J., Model theory for Infinitary Logic, North-Holland, Amsterdam, 1971.Google Scholar
Keisler, H. J. and Morley, M., Elementary extensions of models of set theory. Israel Journal of Mathematics, vol. 5 (1968), pp. 331–348.Google Scholar
Knight, J. F., Montalban, A., and Schweber, N., Computable structures in generic extensions, preprint, 2014.Google Scholar
Kueker, D. W., Abstract elementary classes and infinitary logics. Annals of Pure and Applied Logic, vol. 156 (2008), pp. 274–286.CrossRefGoogle Scholar
Larson, Paul, Scott processes, preprint.Google Scholar
Marker, D., Scott ranks of counterexamples to Vaught’s conjecture, Notes from 2011, http://homepages.math.uic.edu/∼marker/harrington-vaught.pdf.Google Scholar
Marker, D., Model theory and infinitary logic, Notes from 2013, http://homepages.math.uic.edu/∼marker/math512-F13/.Google Scholar
Rosenstein, J., Linear Orderings, Academic Press, New York, 1982.Google Scholar
Shelah, S., Categoricity in ℵ 1of sentences in L ω 1,ω(Q). Israel Journal of Mathematics, vol. 20 (1975), pp. 127–148, 48.CrossRefGoogle Scholar
Shelah, S., Classification Theory and the Number of Nonisomorphic Models, North-Holland, Amsterdam, 1978.Google Scholar
Shelah, S., Classification theory for nonelementary classes. I. the number of uncountable models of ψ ∈ L ω 1ωpart A. Israel Journal of Mathematics, vol. 46 (1983), no. 3, pp. 212–240, 87a.Google Scholar
Shelah, S., Classification of nonelementary classes II, abstract elementary classes, Classification theory (Baldwin, J. T., editor), Proceedings of the USA–Israel Conference on Classification Theory, Chicago, IL, 1985, Lecture Notes in Mathematics, vol. 1292, Springer, Berlin, 1987, pp. 419–497, 88.Google Scholar
Shelah, S., Categoricity of abstract elementary class in two successive cardinals. Israel Journal of Mathematics, vol. 126 (2001), pp. 29–128, 576.CrossRefGoogle Scholar
Shelah, S., Classification Theory for Abstract Elementary Classes, Studies in Logic, College Publications, London, www.collegepublications.co.uk, 2009. Binds together papers 88r, 600, 705, 734 with introduction E53.Google Scholar
Shelah, S., Categoricity of abstract elementary classes: going up inductive step, preprint, 600, 200x.Google Scholar