Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kočinac, Ljubiša D.
and
Scheepers, Marion
2002.
Function spaces and a property of Reznichenko☆☆The work for this paper was done while Scheepers was visiting Kočinac during May/June 1998 at the Department of Mathematics in the Faculty of Philosophy of the University of Niš, Yugoslavia..
Topology and its Applications,
Vol. 123,
Issue. 1,
p.
135.
Scheepers, Marion
and
Tsaban, Boaz
2002.
The combinatorics of Borel covers.
Topology and its Applications,
Vol. 121,
Issue. 3,
p.
357.
Tsaban, Boaz
2005.
Strong γ-sets and other singular spaces.
Topology and its Applications,
Vol. 153,
Issue. 4,
p.
620.
Bartoszyński, Tomek
and
Tsaban, Boaz
2005.
Hereditary topological diagonalizations and the Menger-Hurewicz Conjectures.
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 2,
p.
605.
Kysiak, Marcin
Nowik, Andrzej
and
Weiss, Tomasz
2007.
Special subsets of the reals and tree forcing notions.
Proceedings of the American Mathematical Society,
Vol. 135,
Issue. 9,
p.
2975.
Machura, Michał
and
Tsaban, Boaz
2008.
The combinatorics of the Baer-Specker group.
Israel Journal of Mathematics,
Vol. 168,
Issue. 1,
p.
125.
Bella, Angelo
Bonanzinga, Maddalena
and
Matveev, Mikhail
2009.
Variations of selective separability.
Topology and its Applications,
Vol. 156,
Issue. 7,
p.
1241.
Bingham, N.H.
and
Ostaszewski, A.J.
2010.
Regular variation without limits.
Journal of Mathematical Analysis and Applications,
Vol. 370,
Issue. 2,
p.
322.
Bonanzinga, Maddalena
Cammaroto, Filippo
and
Matveev, Mikhail
2010.
Projective versions of selection principles.
Topology and its Applications,
Vol. 157,
Issue. 5,
p.
874.
Scheepers, Marion
2010.
Gerlits and function spaces.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 47,
Issue. 4,
p.
529.
Orenshtein, Tal
and
Tsaban, Boaz
2013.
Pointwise convergence of partial functions: The Gerlits–Nagy Problem.
Advances in Mathematics,
Vol. 232,
Issue. 1,
p.
311.
Sakai, Masami
and
Scheepers, Marion
2014.
Recent Progress in General Topology III.
p.
751.
Nowik, Andrzej
2020.
On G-transitive version of perfectly meager sets.
Mathematica Moravica,
Vol. 24,
Issue. 1,
p.
63.
POL, ROMAN
and
ZAKRZEWSKI, PIOTR
2021.
COUNTABLY PERFECTLY MEAGER SETS.
The Journal of Symbolic Logic,
Vol. 86,
Issue. 3,
p.
1214.
Caruvana, Christopher
2023.
The Hurewicz property and the Vietoris hyperspace.
Topology and its Applications,
Vol. 338,
Issue. ,
p.
108670.
Tsaban, Boaz
2024.
Function spaces and the Gerlits–Nagy 𝛿-property.
Proceedings of the American Mathematical Society,
Vol. 153,
Issue. 1,
p.
363.
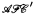 is a set in
is a set in 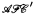 . (
. (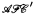 is included in the class of sets always of first category, and includes the class of strong first category sets.)
is included in the class of sets always of first category, and includes the class of strong first category sets.)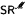 -sets. They also characterize the property (*) introduced by Gerlits and Nagy in terms of older concepts.
-sets. They also characterize the property (*) introduced by Gerlits and Nagy in terms of older concepts.

