Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jech, Thomas
1978.
Logic Colloquium '77.
Vol. 96,
Issue. ,
p.
135.
Kanamori, A.
and
Magidor, M.
1978.
Higher Set Theory.
Vol. 669,
Issue. ,
p.
99.
Nadel, Mark
and
Stavi, Jonathan
1978.
𝐿_{∞}_{𝜆}-equivalence, isomorphism and potential isomorphism.
Transactions of the American Mathematical Society,
Vol. 236,
Issue. 0,
p.
51.
Eklof, Paul C.
and
Mekler, Alan H.
1979.
Stationary logic of finitely determinate structures.
Annals of Mathematical Logic,
Vol. 17,
Issue. 3,
p.
227.
Todorčević, Stevo B.
1981.
Some consequences of MA + ¬wKH.
Topology and its Applications,
Vol. 12,
Issue. 2,
p.
187.
TODORČEVIĆ, S.
1984.
Handbook of Set-Theoretic Topology.
p.
235.
Jech, Thomas J.
1984.
More game-theoretic properties of boolean algebras.
Annals of Pure and Applied Logic,
Vol. 26,
Issue. 1,
p.
11.
Eda, Katsuya
1990.
Boolean powers of abelian groups.
Annals of Pure and Applied Logic,
Vol. 50,
Issue. 2,
p.
109.
Baumgartner, James E.
1991.
On the size of closed unbounded sets.
Annals of Pure and Applied Logic,
Vol. 54,
Issue. 3,
p.
195.
Schlindwein, Chaz
1993.
Suslin's hypothesis does not imply stationary antichains.
Annals of Pure and Applied Logic,
Vol. 64,
Issue. 2,
p.
153.
Huuskonen, Taneli
1995.
Observations about Scott and Karp trees.
Annals of Pure and Applied Logic,
Vol. 76,
Issue. 3,
p.
201.
Moss, Lawrence S.
1995.
Power set recursion.
Annals of Pure and Applied Logic,
Vol. 71,
Issue. 3,
p.
247.
Zapletal, Jindřich
1995.
More on the cut and choose game.
Annals of Pure and Applied Logic,
Vol. 76,
Issue. 3,
p.
291.
Bagaria, Joan
and
D. Friedman, Sy
2001.
Generic absoluteness.
Annals of Pure and Applied Logic,
Vol. 108,
Issue. 1-3,
p.
3.
CUMMINGS, JAMES
FOREMAN, MATTHEW
and
MAGIDOR, MENACHEM
2001.
SQUARES, SCALES AND STATIONARY REFLECTION.
Journal of Mathematical Logic,
Vol. 01,
Issue. 01,
p.
35.
Stanley, M.C.
2001.
Forcing closed unbounded subsets of ω2.
Annals of Pure and Applied Logic,
Vol. 110,
Issue. 1-3,
p.
23.
Di Nasso, Mauro
and
Hrbacek, Karel
2003.
Combinatorial principles in nonstandard analysis.
Annals of Pure and Applied Logic,
Vol. 119,
Issue. 1-3,
p.
265.
Schlindwein, Chaz
2003.
SH plus CH does not imply stationary antichains.
Annals of Pure and Applied Logic,
Vol. 124,
Issue. 1-3,
p.
233.
2004.
2003 European Summer Meeting of the Association for Symbolic Logic. Logic Colloquim '03.
Bulletin of Symbolic Logic,
Vol. 10,
Issue. 02,
p.
234.
Hernández-Hernández, Fernando
and
Ishiu, Tetsuya
2004.
A perfectly normal nonrealcompact space consistent with MAℵ1.
Topology and its Applications,
Vol. 143,
Issue. 1-3,
p.
175.
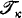 denote {A ⊆ κ ∣ A contains a closed unbounded subset}, then, for any such κ,
denote {A ⊆ κ ∣ A contains a closed unbounded subset}, then, for any such κ, 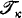 is a κ-additive nonprincipal filter on κ.
is a κ-additive nonprincipal filter on κ.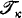 being an ultrafilterκ It is routine to see that this is impossible for κ > ℵ1. However, for κ = ℵ1 the situation is different. If
being an ultrafilterκ It is routine to see that this is impossible for κ > ℵ1. However, for κ = ℵ1 the situation is different. If 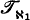 were an ultrafilter, ℵ1 would be a measurable cardinal. As is well-known this is impossible if we assume the axiom of choice; however if ZF + “there exists a measurable cardinal” is consistent, then so is ZF + “ℵ1 is a measurable cardinal” [2]. Furthermore, under the assumption of certain set theoretic axioms (such as the axiom of determinateness or various infinite exponent partition relations)
were an ultrafilter, ℵ1 would be a measurable cardinal. As is well-known this is impossible if we assume the axiom of choice; however if ZF + “there exists a measurable cardinal” is consistent, then so is ZF + “ℵ1 is a measurable cardinal” [2]. Furthermore, under the assumption of certain set theoretic axioms (such as the axiom of determinateness or various infinite exponent partition relations) 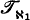 can be proven to be an ultrafilter. (See [3] and [5].)
can be proven to be an ultrafilter. (See [3] and [5].)