Article contents
Zero-one laws with variable probability
Published online by Cambridge University Press: 12 March 2014
Extract
One of this author's favorite theorems has long been the Zero-One law discovered independently by Glebskii et al. [12] and Ron Fagin [10]. Let A be any first-order property of graphs and let µn(A) be the proportion of labelled graphs on n vertices for which A holds. Then

This result has inspired much work by logicians, generally in the direction of showing (1) for some powerful languages. Thus it is known [5] that (1) holds when A is a sentence in fixed point logic and it is known [13] that (1) does not always hold when A is a sentence in second-order monadic logic. Here, however, we explore recent work in a totally different direction. Let G(n, p) denote the random graph on n vertices with edge probability p. (In §2 we define the random structures we will deal with.) A property A is an event in the probability space and Pr[G(n, p) ╞ A] is well defined. When p = 1/2, each labelled graph on n vertices has equal weight so that (1) may be rewritten
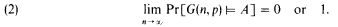
Fagin's proof actually gives that (2) holds for any constant 0 < p < 1.
- Type
- Survey/expository paper
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 9
- Cited by


