Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T13:29:55.810Z Has data issue: false hasContentIssue false
  • English
  • Français

The word problem for cancellation semigroups with zero

Published online by Cambridge University Press:  12 March 2014

Yuri Gurevich  and
Harry R. Lewis
Yuri Gurevich
Affiliation:
Computer and Communication Sciences Department, University of Michigan, Ann Arbor, Michigan 48109
Harry R. Lewis
Affiliation:
Aiken Computation Laboratory, Harvard University, Cambridge, Massachusetts 02138
Get access Rights & Permissions [Opens in a new window]

Extract

By the word problem for some class of algebraic structures we mean the problem of determining, given a finite set E of equations between words (i.e. terms) and an additional equation x = y, whether x = y must hold in all structures satisfying each member of E. In 1947 Post [P] showed the word problem for semigroups to be undecidable. This result was strengthened in 1950 by Turing, who showed the word problem to be undecidable for cancellation semigroups,i.e. semigroups satisfying the cancellation property

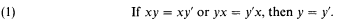
Novikov [N] eventually showed the word problem for groups to be undecidable.

(Many flaws in Turing's proof were corrected by Boone [B]. Even after his corrections, at least one problem remains; the sentence on line 16 of p. 502 of [T] does not follow if one relation is principal and the other is a commutation relation. A corrected and somewhat simplified version of Turing's proof can be built on the construction given here.)

In 1966 Gurevich [G] showed the word problem to be undecidable for finite semigroups. However, this result on finite structures has not been extended to cancellation semigroups or groups; indeed it is easy to see that a finite cancellation semigroup is a group, so both questions are the same. We do not here settle the word problem for finite groups, but we do show that the word problem is undecidable for finite semigroups with zero (that is, having an element 0 such that x0 = 0x = 0 for all x) satisfying an approximation to the cancellation property (1).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 1 , March 1984 , pp. 184 - 191
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Boone, William W., An analysis of Turing's ‘The word problem in semi-groups with cancellation’. Annals of Mathematics, vol. 67 (1958), pp. 195–202.CrossRefGoogle Scholar
[G]Gurevich, Yuri, The word problem for certain classes of semigroups, Algebra and Logic, vol. 5 (1966), pp. 25–35.Google Scholar
[GL]Gurevich, Yuri and Lewis, Harry R., The inference problem for template dependencies, Proceedings of the ACM SIGACT-SIGMOD Conference on Principles of Database Systems, Los Angeles, 1982, Association for Computing Machinery, New York, 1982; revised version, to appear in Information and Control.Google Scholar
[N]Novikov, P. S., On the algorithmic unsolvability of the word problem in group theory, Trudy Matematicheskogo Instituta imeni V. A. Steklova, vol. 44 (1955). (Russian)Google Scholar
[P]Post, Emil L., Recursive unsolvability of a problem of Thue, this Journal, vol. 12 (1947), pp. 1–11.Google Scholar
[R]Rogers, Hartley, Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[S1]Slobodskoi, A. M., Unsolvability of the universal theory of finite groups, Algebra and Logic, vol. 20 (1981), pp. 139–156.CrossRefGoogle Scholar
[Sm]Smullyan, Raymond M., Theory of formal systems, Annals of Mathematics Studies, No. 47, Princeton University Press, Princeton, N.J., 1961.CrossRefGoogle Scholar
[T]Turing, Alan M., The word problem for semigroups with cancellation, Annals of Mathematics, vol. 52 (1950), pp. 491–505.CrossRefGoogle Scholar