Let ${\cal S}$ be a Scott set, or even an ω-model of WWKL. Then for each A ε S, either there is X ε S that is weakly 2-random relative to A, or there is X ε S that is 1-generic relative to A. It follows that if A1,…,An ε S are noncomputable, there is X ε S such that each Ai is Turing incomparable with X, answering a question of Kučera and Slaman. More generally, any ∀∃ sentence in the language of partial orders that holds in 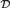${\cal D}$ also holds in 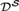${{\cal D}^{\cal S}}$, where 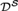${{\cal D}^{\cal S}}$ is the partial order of Turing degrees of elements of ${\cal S}$.