Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T09:00:38.353Z Has data issue: false hasContentIssue false
  • English
  • Français

A WEAKLY 2-GENERIC WHICH BOUNDS A MINIMAL DEGREE

Published online by Cambridge University Press:  04 November 2019

RODNEY G. DOWNEY  and
SATYADEV NANDAKUMAR
RODNEY G. DOWNEY
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY WELLINGTON P. O. BOX 600, WELLINGTON, NEW ZEALAND E-mail: [email protected]
SATYADEV NANDAKUMAR
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE AND ENGINEERING INDIAN INSTITUTE OF TECHNOLOGY KANPUR KANPUR208016, UTTAR PRADESH, INDIA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Jockusch showed that 2-generic degrees are downward dense below a 2-generic degree. That is, if a is 2-generic, and 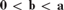$0 < {\bf{b}} < {\bf{a}}$, then there is a 2-generic g with 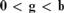$0 < {\bf{g}} < {\bf{b}}.$ In the case of 1-generic degrees Kumabe, and independently Chong and Downey, constructed a minimal degree computable from a 1-generic degree. We explore the tightness of these results.

We solve a question of Barmpalias and Lewis-Pye by constructing a minimal degree computable from a weakly 2-generic one. While there have been full approximation constructions of 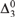${\rm{\Delta }}_3^0$ minimal degrees before, our proof is rather novel since it is a computable full approximation construction where both the generic and the minimal degrees are 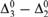${\rm{\Delta }}_3^0 - {\rm{\Delta }}_2^0$.

Keywords

Primary 03D28Secondary 03D3003D55Turing degreeminimal degreeweakly 2-generic
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 4 , December 2019 , pp. 1326 - 1347
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barmpalias, G., Day, A. R., and Lewis-Pye, A. E. M., The typical Turing degree. Proceedings of the London Mathematical Society. Third Series, vol. 109 (2014), no. 1, pp. 1–39.CrossRefGoogle Scholar
Barmpalias, G. and Lewis-Pye, A., The information content of typical reals, Turing’s Revolution (Summerauga, G. and Strahm, T., editors), Birkhäuser/Springer, Cham, 2015, pp. 207–224.CrossRefGoogle Scholar
Chong, C. T. and Downey, R. G., Minimal degrees recursive in 1-generic degrees. Annals of Pure and Applied Logic, vol. 48 (1990), pp. 215–225.CrossRefGoogle Scholar
Chong, C. T. and Jockusch, C. G., Minimal degrees and 1-generic sets below $0\prime$., Computation and Proof Theory (Aachen, 1983), Lecture Notes in Mathematics, vol. 1104, Springer, Berlin, 1984, pp. 63–77.Google Scholar
Chong, C. T. and Downey, R. G., Degrees bounding minimal degrees. Mathematical Proceedings of the Cambridge Philosophical Society, vol. 105 (1989), pp. 211–222.CrossRefGoogle Scholar
Cooper, S. B., Minimal degrees and the jump operator, this Journal, vol. 38 (1973), pp. 249–271.Google Scholar
Downey, R. and Yu, L., Arithmetical Sacks forcing. Archive for Mathematical Logic, vol. 45 (2006), no. 6, pp. 715–720.CrossRefGoogle Scholar
Downey, R. G., On $\pi _1^0$classes and their ranked points . Notre Dame Journal of Formal Logic , vol. 32 (1991), pp. 499–512.CrossRefGoogle Scholar
Downey, R. G. and Hirschfeldt, D., Algorithmic Randomness and Complexity, Springer, New York, 2010.CrossRefGoogle Scholar
Friedberg, R. M., Three theorems on recursive enumeration. I. Decomposition. II. Maximal set. III. Enumeration without duplication, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
Haught, C. A., The degrees below a 1-generic degree $< 0\prime$., this Journal, vol. 51 (1986), no. 3, pp. 770–777.Google Scholar
Jokusch, C., Degrees of generic sets, Recursion Theory: Its Generalizations and Applications (Drake, F. R. and Wainer, S. S., editors), Cambridge University Press, New York, 1980, pp. 110–139.CrossRefGoogle Scholar
Kumabe, M., A 1-generic degree which bounds a minimal degree, this Journal, vol. 55 (1990), pp. 733–743.Google Scholar
Kurtz, S. A., Randomness and genericity in the degrees of unsolvability, Ph.D. thesis, University of Illinois at Urbana-Champaign, ProQuest LLC, Ann Arbor, MI, 1981.Google Scholar
McInerney, M., Topics in algorithmic randomness and computability theory, Ph.D. thesis, Victoria University Wellington, New Zealand, 2016.Google Scholar
Shoenfield, J. R., Degrees of Unsolvability, New York, 1971, North-Holland Mathematics Studies, No. 2.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees, Springer, Berlin, Heidelberg, 1987.CrossRefGoogle Scholar
Spector, C., On degrees of recursive unsolvability. Annals of Mathematics. Second Series, vol. 64 (1956), pp. 581–592.CrossRefGoogle Scholar
Yates, C. E. M., Initial segments of the degrees of unsolvability Part II: Minimal degrees, this Journal, vol. 35 (1970), pp. 243–266.Google Scholar