Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T17:03:16.577Z Has data issue: false hasContentIssue false
  • English
  • Français

A version of p-adic minimality

Published online by Cambridge University Press:  12 March 2014

Raf Cluckers  and
Eva Leenknegt
Raf Cluckers
Affiliation:
Université Lille 1, Laboratoiré Painlevé, CNRS - UMR 8524, Cité Scientifique, 59655 Villeneuve d'Ascq Cedex, France Katholieke Universiteit Leuven, Department of Mathematics, Celestijnenlaan 200B, B-3001 Leuven, Belgium, E-mail: [email protected], URL: http://math.univ-lille1.fr/~cluckers
Eva Leenknegt
Affiliation:
Purdue University, Department of Mathematics, 150 N. University Street, West Lafayette, IN 47907-2067, USA, E-mail: [email protected], URL: http://www.math.purdue.edu/~eleenkne
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a very weak language 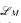on p-adic fields K, which is just rich enough to have exactly the same definable subsets of the line K that one has using the ring language. (In our context, definable always means definable with parameters.) We prove that the only definable functions in the language 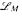are trivial functions. We also give a definitional expansion 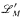of 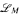in which K has quantifier elimination, and we obtain a cell decomposition result for 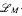-definable sets.

Our language 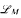can serve as a p-adic analogue of the very weak language (<) on the real numbers, to define a notion of minimality on the field of p-adic numbers and on related valued fields. These fields are not necessarily Henselian and may have positive characteristic.

Keywords

p-adic numbersquantifier eliminationcell decompositionP-minimalityo-minimalitydefinability
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 2 , June 2012 , pp. 621 - 630
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Ax, J. and Kochen, S., Diophantine problems over local fields II. A complete set of axioms for p-adic number theory, American Journal of Mathematics, vol. 87 (1965), pp. 631–648.CrossRefGoogle Scholar
[2] Cluckers, R., Analytic p-adic cell decomposition and integrals. Transactions of the American Mathematical Society, vol. 356 (2003), no. 4, pp. 1489–1499.Google Scholar
[3] Cluckers, R. and Lipshitz, L., Fields with analytic structure. Journal of the European Mathematical Society, vol. 13 (2011), pp. 1147–1223.CrossRefGoogle Scholar
[4] Cluckers, Raf, Classification of semi-algebraic p-adic sets up to semi-algebraic bijection, Journal für die Reine und Angewandte Mathematik. vol. 540 (2001). pp. 105–114.Google Scholar
[5] Cluckers, Raf and Loeser, François, b-minimality. Journal of Mathematical Logic, vol. 7 (2007), no. 2, pp. 195–227.Google Scholar
[6] Denef, J. and van den Dries, L., p-adic and real subanalytic sets. Annals of Mathematics. Second Series, vol. 128 (1988), no. 1, pp. 79–138.CrossRefGoogle Scholar
[7] Denef, Jan. p-adic semi-algebraic sets and cell decomposition. Journal für die Reine und Angewandte Mathematik. vol. 369 (1986), pp. 154–166.Google Scholar
[8] van den Dries, L., Haskell, D., and Macpherson, D., One-dimensional p-adic subanalytic sets, Journal of the London Mathematical Society, vol. 59 (1999). no. 1. pp. 1–20.CrossRefGoogle Scholar
[9] Haskell, Deirdre and Macpherson, Dugald, A version of o-minimality for the p-adics, this Journal, vol. 62 (1997), no. 4, pp. 1075–1092.Google Scholar
[10] Liu, Nianzheng, Semilinear cell decomposition, this Journal, vol. 59 (1994), no. 1, pp. 199–208.Google Scholar
[11] Macintyre, A., On definable subsets of p-adic fields, this Journal, vol. 41 (1976), pp. 605–610.Google Scholar
[12] Macpherson, D. and Steinhorn, C., On variants of o-minimality, Annals of Pure and Applied Logic, vol. 79 (1996), no. 2, pp. 165–209.CrossRefGoogle Scholar
[13] Mourgues, Marie-Hélène, Cell decomposition for P-minimal fields, Mathematical Logic Quarterly, vol. 55 (2009), no. 5, pp. 487–492.CrossRefGoogle Scholar
[14] Prestel, A. and Roquette, P., Formally p-adic fields, Lecture Notes in Mathematics, Springer-Verlag, Berlin, 1984.Google Scholar
[15] Scowcroft, Philip, Cross-sections for p-adically closed fields, Journal of Algebra, vol. 183 (1996), no. 3, pp. 913–928.Google Scholar
[16] Scowcroft, Philip and van den Dries, Lou, On the structure of semialgebraic sets over p-adic fields, this Journal, vol. 53 (1988), no. 4, pp. 1138–1164.Google Scholar