Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T06:51:49.580Z Has data issue: false hasContentIssue false
  • English
  • Français

Up to equimorphism, hyperarithmetic is recursive

Published online by Cambridge University Press:  12 March 2014

Antonio Montalbán
Antonio Montalbán*
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853, USA, E-mail: [email protected] URL: www.math.cornell.edu/~antonio
Get access Rights & Permissions [Opens in a new window]

Abstract

Two linear orderings are equimorphic if each can be embedded into the other. We prove that every hyperarithmetic linear ordering is equimorphic to a recursive one.

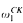On the way to our main result we prove that a linear ordering has Hausdorff rank less than if and only if it is equimorphic to a recursive one. As a corollary of our proof we prove that, given a recursive ordinal α, the partial ordering of equimorphism types of linear orderings of Hausdorff rank at most α ordered by embeddablity is recursively presentable.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 70 , Issue 2 , June 2005 , pp. 360 - 378
Copyright
Copyright © Association for Symbolic Logic 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AB99] Abraham, Uri and Bonnet, Rorert, Hausdorff's theorem for posets that satisfy the finite antichain property, Fundamenta Mathematicae, vol. 159 (1999), no. 1, pp. 51–69.CrossRefGoogle Scholar
[AK00] Ash, C. J. and Knight, J., Computable structures and the hyperarithmetical hierarchy, Elsevier Science, 2000.Google Scholar
[BP82] Bonnet, R. and Pouzet, M., Linear extensions of ordered sets, Ordered sets (Banff, Alta., 1981), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 83, Reidel, Dordrecht, 1982, pp. 125–170.CrossRefGoogle Scholar
[Clo89] Cloth, P., The metamathematics of scattered linear orderings, Archive for Mathematical Logic, vol. 29 (1989), no. 1, pp. 9–20.CrossRefGoogle Scholar
[Clo90] Cloth, P., The metamathematics of Fraïssé's order type conjecture, Recursion theory week (Oberwolfach, 1989), Lecture Notes in Mathematics, vol. 1432, Springer, Berlin, 1990, pp. 41–56.CrossRefGoogle Scholar
[Dow98] Downey, R. G., Computahility theory and linear orderings, Handbook of recursive mathematics, vol. 2 (Ershov, Yu. L. et al., editors). Studies in Logic and the Foundations of Mathematics, vol. 139, North-Holland, Amsterdam, 1998, pp. 823–976.Google Scholar
[DHLS03] Downey, Rodney G., Hirschfeldt, Denis R., Lempp, Steffen, and Solomon, Reed, Computahility-theoretic and proof-theoretic aspects of partial and linear orderings, Israel Journal of Mathematics, vol. 138 (2003), pp. 271–352.CrossRefGoogle Scholar
[Fei67] Feiner, Lawrence, Orderings and Boolean Algebras not isomorphic to recursive ones, Ph.D. thesis, MIT, Cambridge, MA, 1967.Google Scholar
[Fei70] Feiner, Lawrence, Hierarchies of Boolean algebras, this Journal, vol. 35 (1970), pp. 365–374.Google Scholar
[Fra48] Fraïssé, Roland, Sur la comparaison des types d'ordres, Comptes Rendus de l'Académie des Sciences. Paris vol. 226 (1948), pp. 1330–1331.Google Scholar
[Hes06] Hessenberg, G., Grundbegriffe der Mengenlehre, Abhandlungen der Fries'schen Schule N.S., vol. 1 (1906), pp. 479–706.Google Scholar
[JS91] Jockusch, Carl G. Jr., and Soare, Robert I., Degrees of orderings not isomorphic to recursive linear orderings, Annals of Pure and Applied Logic, vol. 52 (1991), no. 1-2, pp. 39–64, International Symposium on Mathematical Logic and its Applications (Nagoya, 1988).CrossRefGoogle Scholar
[Jul69] Jlillien, Pierre, Contribution à l'étude des types d'ordre dispersés. Ph.D, thesis, Marseille, 1969.Google Scholar
[Lav71] Laver, Richard, On Fruïssé's order type conjecture, Annals of Mathematics. Second Series, vol. 93 (1971), pp. 89–111.CrossRefGoogle Scholar
[Ler81] Lerman, Manuel, On recursive linear orderings, Logic Year 1979–80 (Proceedings of Seminars and Conferences in Mathematical Logic, University of Connecticut, Starrs, Connecticut, 1979/80), Lecture Notes in Mathematics, vol. 859, Springer, Berlin, 1981, pp. 132–142.CrossRefGoogle Scholar
[Mar05] Marcone, Alberto, WQO and BQO theory in subsystems of second order arithmetic, Reverse mathematics (Simpson, S., editor). Lecture Notes in Logic, vol. 21, AK Peters, 2005, pp. 303–330.Google Scholar
[Mil85] Milner, E. C., Basic wqo- and bqo-theory, Graphs and order (Banff, Alta., 1984), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 147, Reidel, Dordrecht, 1985, pp. 487–502.CrossRefGoogle Scholar
[Mon] Montalbán, Antonio, Equivalence between Fraïssé s conjecture and Jullien's theorem, To appear.Google Scholar
[Mon05] Montalbán, Antonio, Beyond the arithmetic, Ph.D. thesis, Cornell University, 2005, In preparation.Google Scholar
[Nas68] Nash-Williams, C. St. J. A., On better-quasi-ordering transfinite sequences, Proceedings of the Cambridge Philosophical Society, vol. 64 (1968), pp. 273–290.CrossRefGoogle Scholar
[Ros82] Rosenstein, Joseph, Linear orderings, Academic Press, New York – London, 1982.Google Scholar
[Sac90] Sacks, Gerald E., Higher recursion theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
[Sho93] Shore, Richard A., On the strength of Fraïssé's conjecture, Logical methods> (Ithaca, NY, 1992), Progress in Computer Science and Applied Logic, vol. 12, Birkhäuser Boston, Boston, MA, 1993, pp. 782–813.Google Scholar
[Sim99] Simpson, Stephen G., Subsystems of second order arithmetic, Springer, 1999.CrossRefGoogle Scholar
[Spe55] Spector, Clifford, Recursive well-orderings, this Journal, vol. 20 (1955), pp. 151–163.Google Scholar