Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T05:56:22.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal recursion theoretic properties of r.e. preordered structures

Published online by Cambridge University Press:  12 March 2014

Franco Montagna  and
Andrea Sorbi
Franco Montagna
Affiliation:
Dipartimento Di Matematica, Università Di Siena, 53100 Siena, Italia
Andrea Sorbi
Affiliation:
Dipartimento Di Matematica, Università Di Siena, 53100 Siena, Italia
Get access Rights & Permissions [Opens in a new window]

Extract

When dealing with axiomatic theories from a recursion-theoretic point of view, the notion of r.e. preordering naturally arises. We agree that an r.e. preorder is a pair 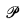= 〈P, ≤P〉 such that P is an r.e. subset of the set of natural numbers (denoted by ω), ≤P is a preordering on P and the set {〈;x, y〉: x ≤Py} is r.e.. Indeed, if 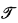is an axiomatic theory, the provable implication of 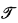yields a preordering on the class of (Gödel numbers of) formulas of .

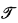Of course, if ≤P is a preordering on P, then it yields an equivalence relation ~P on P, by simply letting x ~Py iff x ≤Py and y ≤Px. Hence, in the case of P = ω, any preordering yields an equivalence relation on ω and consequently a numeration in the sense of [4]. It is also clear that any equivalence relation on ω (hence any numeration) can be regarded as a preordering on ω. In view of this connection, we sometimes apply to the theory of preorders some of the concepts from the theory of numerations (see also Eršov [6]).

Our main concern will be in applications of these concepts to logic, in particular as regards sufficiently strong axiomatic theories (essentially the ones in which recursive functions are representable). From this point of view it seems to be of some interest to study some remarkable prelattices and Boolean prealgebras which arise from such theories. It turns out that these structures enjoy some rather surprising lattice-theoretic and universal recursion-theoretic properties.

After making our main definitions in §1, we examine universal recursion-theoretic properties of some r.e. prelattices in §2.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 2 , June 1985 , pp. 397 - 406
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bernardi, C., On the relation provable equivalence and on partitions in effectively inseparable sets, Studia Logica vol. 40 (1981), pp. 29–37.CrossRefGoogle Scholar
[2]Bernardi, C. and Montagna, F., Equivalence relations induced by extensional formulae: classification by means of a new fixed point property, Fundamenta Mathematicae (to appear).Google Scholar
[3]Bernardi, C. and Sorbi, A., Classifying positive equivalence relations, this Journal, vol. 48 (1983), pp. 529–538.Google Scholar
[4]Eršov, Ju. L., Theorie der Numerierungen. I, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 19 (1973), pp. 289–388.CrossRefGoogle Scholar
[5]Eršov, Ju. L., Theorie der Numerierungen. II, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 21 (1975), pp. 473–584.CrossRefGoogle Scholar
[6]Eršov, Ju. L., Theorie der Numerierungen. III, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 23 (1977), pp. 289–371.Google Scholar
[7]Grätzer, G., Lattice theory, Freeman, San Francisco, California, 1971.Google Scholar
[8]Kripke, S. and Pour-El, M. B., Deduction preserving recursive isomorphism between theories, Fundamenta Mathematicae, vol. 61 (1967), pp. 141–163.Google Scholar
[9]Montagna, F., Relatively precomplete numerations and arithmetic, Journal of Philosophical Logic, vol. 11 (1982), pp. 419–430.CrossRefGoogle Scholar
[10]Montagna, F., A completeness result for fixed point algebras, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik (to appear).Google Scholar
[11]Rogers, H., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[12]Smoryński, C., The incompleteness theorems, Handbook of mathematical logic (Barwise, J., editor), North-Holland, Amsterdam 1977, pp. 821–865.CrossRefGoogle Scholar
[13]Visser, A., Numerations, λ-calculus and arithmetric, To H. B. Curry: Essays on combinatory logic, lambda calculus and formalism (Seldin, J. P. and Hindley, J. R., editors), Academic Press, London, 1980, pp. 259–284.Google Scholar