Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-06T07:51:08.807Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIVERSAL CLASSES NEAR 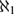${\aleph _1}$

Published online by Cambridge University Press:  21 December 2018

MARCOS MAZARI-ARMIDA  and
SEBASTIEN VASEY
MARCOS MAZARI-ARMIDA
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES CARNEGIE MELLON UNIVERSITY PITTSBURGH, PENNSYLVANIA, USA E-mail: [email protected]: http://www.math.cmu.edu/∼mmazaria/
SEBASTIEN VASEY
Affiliation:
DEPARTMENT OF MATHEMATICS HARVARD UNIVERSITY CAMBRIDGE, MASSACHUSETTS, USA E-mail: [email protected]: http://math.harvard.edu/∼sebv/
Get access Rights & Permissions [Opens in a new window]

Abstract

Shelah has provided sufficient conditions for an 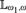${\Bbb L}_{\omega _1 ,\omega } $-sentence ψ to have arbitrarily large models and for a Morley-like theorem to hold of ψ. These conditions involve structural and set-theoretic assumptions on all the 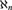${\aleph _n}$’s. Using tools of Boney, Shelah, and the second author, we give assumptions on 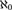${\aleph _0}$ and 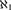${\aleph _1}$ which suffice when ψ is restricted to be universal:

Theorem.Assume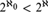${2^{{\aleph _0}}} < {2^{{\aleph _1}}}$. Let ψ be a universal 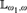${\Bbb L}_{\omega _1 ,\omega } $-sentence.

  1. (1) If ψ is categorical in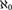${\aleph _0}$and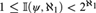$1 \leqslant {\Bbb L}\left( {\psi ,\aleph _1 } \right) < 2^{\aleph _1 } $, then ψ has arbitrarily large models and categoricity of ψ in some uncountable cardinal implies categoricity of ψ in all uncountable cardinals.

  2. (2) If ψ is categorical in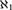${\aleph _1}$, then ψ is categorical in all uncountable cardinals.

The theorem generalizes to the framework of 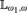${\Bbb L}_{\omega _1 ,\omega } $-definable tame abstract elementary classes with primes.

Keywords

Primary 03C48Secondary 03C4503C5203C5503C75abstract elementary classesuniversal classescategoricitygood framestamenessprime models
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 4 , December 2018 , pp. 1633 - 1643
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ackerman, N., Boney, W., and Vasey, S., Categoricity in multiuniversal classes, preprint, arXiv:1804.09067v2.Google Scholar
Baldwin, J., Categoricity, American Mathematical Society, Providence, RI, 2009.CrossRefGoogle Scholar
Baldwin, J. and Kolesnikov, A., Categoricity, amalgamation, and tameness. Israel Journal of Mathematics, vol. 170 (2009), no. 1, pp. 411–443.CrossRefGoogle Scholar
Baldwin, J. and Lachlan, A., On universal Horn classes categorical in some infinite power. Algebra Universalis (Fasc. 1), vol. 3 (1973), pp. 98–111.CrossRefGoogle Scholar
Boney, W., Tameness and extending frames, Journal of Mathematical Logic, vol. 14 (2014), no. 2, p. 1450007, 27 pp.CrossRefGoogle Scholar
Boney, W. and Vasey, S., Tameness and frames revisited, this Journal, vol. 83 (2017), no. 3, pp. 995–1021.Google Scholar
Grossberg, R., Classification theory for abstract elementary classes, Logic and Algebra, vol. 302 (Zhang, Y., editor), American Mathematical Society, Providence, RI, 2002, pp. 165–204.CrossRefGoogle Scholar
Grossberg, R. and VanDieren, M., Galois-stability for tame abstract elementary classes. Journal of Mathematical Logic, vol. 6 (2006), no. 1, pp. 25–49.CrossRefGoogle Scholar
Hart, B. and Shelah, S., Categoricity over P for first order T or categoricity for $\phi \in {{\rm{L}}_{{\omega _1}\omega }}$ can stop at ${\aleph _k}$ while holding for ${\aleph _0}, \ldots ,{\aleph _{k - 1}}$. Israel Journal of Mathematics , vol. 70 (1990), pp. 219–235.Google Scholar
Hyttinen, T. and Kangas, K., Categoricity and universal classes, preprint. URL: https://arxiv.org/abs/1712.08532v2.Google Scholar
Hyttinen, T. and Kesälä, M., Independence in finitary abstract elementary classes. Annals of Pure and Applied Logic, vol. 143 (2006), pp. 103–138.CrossRefGoogle Scholar
Jarden, A. and Shelah, S., Non-forking frames in abstract elementary classes. Annals of Pure and Applied Logic, vol. 164 (2013), pp. 135–191.CrossRefGoogle Scholar
Keisler, H. J., Logic with the quantifier “there exists uncountable many”. Annals of Mathematical Logic, vol. 1 (1970), no. 1, pp. 1–93.CrossRefGoogle Scholar
Kirby, J., On quasiminimal excellent classes, this JOURNAL, vol. 75 (2010), no. 2, pp. 551–564.Google Scholar
Shelah, S., Categoricity in ${\aleph _1}$ of sentences in ${L_{{\omega _1},\omega }}\left( Q \right)$. Israel Journal of Mathematics , vol. 20 (1975), pp. 127–148.CrossRefGoogle Scholar
Shelah, S., Classification theory for nonelementary classes, I. The number of uncountable models of $\psi \in {L_{{\omega _1},\omega }}$. Part A. Israel Journal of Mathematics, vol. 46 (1983), pp. 212–240.CrossRefGoogle Scholar
Shelah, S., Classification theory for nonelementary classes, I. The number of uncountable models of $\psi \in {L_{{\omega _1},\omega }}$. Part B. Israel Journal of Mathematics, vol. 46 (1983), pp. 241–273.CrossRefGoogle Scholar
Shelah, S., Classification of nonelementary classes, II. Abstract elementary classes, Classification Theory (Baldwin, J., editor), Springer-Verlag, Chicago, IL, 1987, pp. 419–497.CrossRefGoogle Scholar
Shelah, S., Universal classes, Classification Theory (Baldwin, J., editor), Springer-Verlag, Chicago, IL, 1987, pp. 264–418.CrossRefGoogle Scholar
Shelah, S., Classification Theory for Abstract Elementary Classes, vol. 1 & 2, Mathematical Logic and Foundations, no. 18 & 20, College Publications, 2009.Google Scholar
Shelah, S. and Vasey, S., Abstract elementary classes stable in ${\aleph _0}$. Annals of Pure and Applied Logic, vol. 169 (2018), no. 7, pp. 565–587.CrossRefGoogle Scholar
Tarski, A., Contributions to the theory of models I. Indagationes Mathematicae, vol. 16 (1954), pp. 572–581.CrossRefGoogle Scholar
Vasey, S., Infinitary stability theory. Archive for Mathematical Logic, vol. 55 (2016), no. 3–4, pp. 562–592.CrossRefGoogle Scholar
Vasey, S., Downward categoricity from a successor inside a good frame. Annals of Pure and Applied Logic, vol. 168 (2017), no. 3, pp. 651–692.CrossRefGoogle Scholar
Vasey, S., Shelah’s eventual categoricity conjecture in tame AECs with primes. Mathematical Logic Quarterly, vol. 64 (2018), no. 1–2, pp. 25–36.CrossRefGoogle Scholar
Vasey, S., Shelah’s eventual categoricity conjecture in universal classes: Part I. Annals of Pure and Applied Logic, vol. 168 (2017), no. 9, pp. 1609–1642.CrossRefGoogle Scholar
Vasey, S., Shelah’s eventual categoricity conjecture in universal classes: Part II. Selecta Mathematica, vol. 23 (2017), no. 2, pp. 1469–1506.CrossRefGoogle Scholar
Zilber, B., Pseudo-exponentiation on algebraically closed fields of characteristic zero. Annals of Pure and Applied Logic, vol. 132 (2005), pp. 67–95.CrossRefGoogle Scholar